1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 8 Обработка данных

- На этом и построен мой метод дедукции. - А как это выглядит на практике?

К/ф "Приключения Шерлока Холмса и доктора Ватсона. Знакомство"

В этой главе обсуждается несколько вопросов, связанных с обработкой данных. Разумеется, что эта тема многогранна и практически неисчерпаема. Здесь мы остановимся только на наиболее интересных и, вместе с тем, не очень сложных задачах, при решении которых целесообразно использовать приложение Matlab.

Одной из наиболее часто встречающихся является задача интерполирования. Идеологически близка к ней задача аппроксимации. Именно их и рассмотрим в начале этой главы.

Интерполяционные полиномы

- Нашел!

- Что именно? - Формулу!

К/ф "Приключения Шерлока Холмса и доктора Ватсона. Знакомство"

Обычно о задаче интерполирования говорят в том случае, если имеется некоторый набор табличных значений функции, и по этим табличным значениям необходимо восстановить или просто построить некоторую аналитическую зависимость. Задача важна во многих отношениях и может иметь разную исходную постановку. Начнем с наиболее простых случаев.

Предположим, что имеется набор узловых точек x1 , x2 , ..., xn и значения y1 , y2 , ..., yn некоторой функции в этих узловых точках. Если речь идет о задаче интерполирования, то она может быть сформулирована так: необходимо построить (в соответствии с определенными критериями) некоторую функцию f (x), такую, что эта функция в узловых точках x1 , x2 , ..., xn принимает значения y1 , y2 , ..., yn , то есть f (xk ) = yk для всех индексов k от 1 до n .

Этого критерия совершенно недостаточно, чтобы однозначно определить интерполяционную функцию f (x). Необходимо уточнить ее вид. Очень часто функцию f (x) ищут в виде полинома. Степень полинома выбирается в соответствии с количеством узловых точек. Если узловых точек n , то степень интерполяционного полинома равняется n −1. Такой полином име-

311

Самоучитель Matlab

ет вид f(x) = a1xn−1 +a2xn−2 +a3xn−3 +... +an−1x +an и содержит n параметров a1 , a2 , ..., an , благодаря которым удается добиться того, чтобы

интерполяционный полином проходил через базовые точки (xk,yk ) (индекс k = 1,2,...,n ). Фактически задача сводится к определению коэффициентов интерполяционного полинома на основании значений базовых точек. Существуют различные алгоритмы решения такой задачи, но в нашем случае все существенно упрощается, поскольку в Matlab есть специальные функции для построения интерполяционного полинома и выполнения сопутствующих вычислений. Тем не менее, кратко рассмотрим математическую суть проблемы.

торую следует решать относительно коэффициентов a1 , a2 , ..., an . Система

то есть для элементов W (индексы i, j = 1,2,...,n ) этой матрицы имеет место соотношение Wij =ij xin−j . Для вычисления матрицы Вандермонда в Matlab предназначена функция vander(). Аргументом функции указыва-

полинома можно вычислить в любой точке – для этого в Matlab тоже есть специальные функции. Рассмотрим документ, представленный в документе на рис. 8.1.

Командами x=[0,0.2,0.4,0.7,0.9,1.2,1.5] и y=cos(2*pi*x)./ (1+x) задаются узловые точки и значения функции в узловых точках соот-

ветственно. В данном случае табулируется функция y(x) = . Ма-

трицу Вандермонда вычисляем командой W=vander(x). Коэффициенты

312

Глава 8. Обработка данных

Рис. 8.1. Вычисление интерполяционного полинома

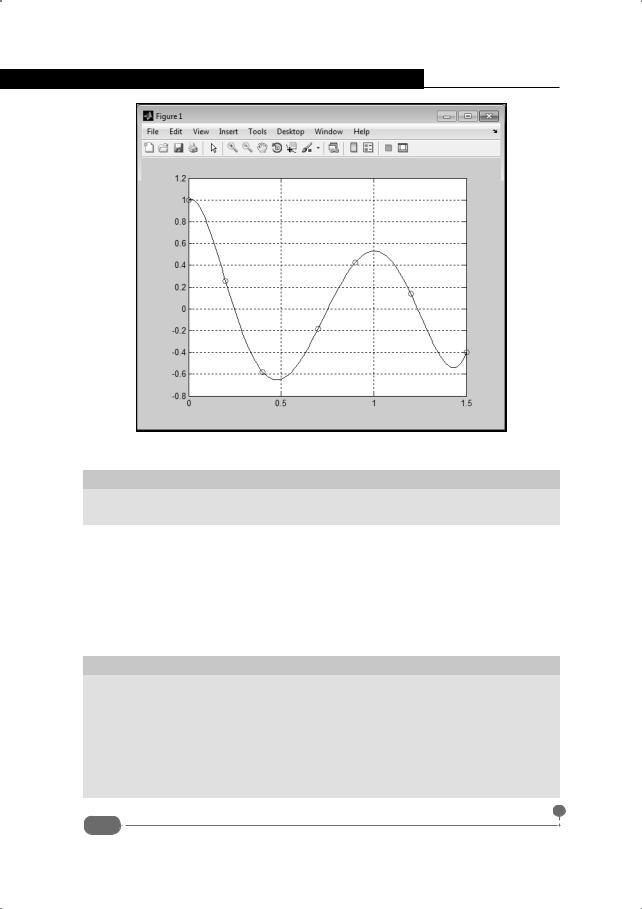
интерполяционного полинома вычисляются командой a=y*inv(W.'). На этом процесс вычисления интерполяционного полинома собственно и заканчивается. Дальнейший код предназначен для иллюстрации полученного результата. В частности, командами z=0:0.01:1.5 и f=polyval(a,z) создаем набор точек, по которым будем строить полиномиальную кривую. Командой plot(x,y,'ro') на графике отображаем базовые точки, затем с помощью инструкции hold on переходим в режим удержания графики и отображаем интерполяционную кривую с помощью команды plot(z,f,'k-'). Инструкция grid on нужна для отображения координатной сетки. На рис. 8.2 представлен график с базовыми точками и кривая, построенная на основе интерполяционного полинома.

Кривая достаточно плавная и проходит через все базовые точки, как и следовало ожидать для интерполяционной кривой. Тем не менее, ситуация далеко не всегда такая идиллическая. Об этом речь еще будет идти.

Для выполнения полиномиальной интерполяции в Matlab может использоваться функция polyfit().

313

Самоучитель Matlab

Рис. 8.2. Базовые точки и интерполяционная кривая

На заметку

Строго говоря, функция polyfit() предназначена для выполнения аппроксимации. Частным случаем задачи аппроксимации является задача интерполяции.

Аргументами функции polyfit() передаются список узловых точек и список значений интерполируемой функции в этих точках. Также указывается степень интерполяционного полинома. В качестве результата возвращается список с коэффициентами полинома. Чтобы это был именно интерполяционный полином, необходимо, чтобы степень этого полинома была на единицу меньше количества узловых точек. В противном случае полученный полином будет аппроксимировать табличные данные.

На заметку

При вычислении полинома функцией polyfit() используется метод наименьших квадратов. Вычисляется полином заданной степени, который наилучшим образом аппроксимирует табличные данные. При этом в общем случае полиномиальная кривая не обязательно проходит через базовые точки. Если степень полинома на единицу меньше количества базовых точек, то при аппроксимации метод наименьших квадратов позволяет построить полином, кривая которого проходит через все базовые точки. То есть фактически такой полином является интерполяционным.

314

Глава 8. Обработка данных

Пример использования функции polyfit() для создания интерполяционного полинома приведен в документе на рис. 8.3.

Рис. 8.3. Создание интерполяционного полинома с помощью функции polyfit()

Здесь мы использовали такую последовательность команд:

>>x=-5:1:5;

>>y=sin(pi*x./2)./(1+x.^2);

>>P=polyfit(x,y,length(x)-1);

>>z=-5.1:0.01:5.1;

>>plot(x,y,'ks')

>>hold on

>>grid on

>>plot(z,polyval(P,z),'r-')

>>title('Интерполяционный полином')

>>P2=polyfit(x,y,5);

>>plot(z,polyval(P2,z),'k-.')

>>legend('базовые точки','интерполяция','аппроксимация')

Первые две команды (x=-5:1:5 и y=sin(pi*x./2)./(1+x.^2)) создают наборы точек, на основе которых будет строиться интерполяционный полином. Командой P=polyfit(x,y,length(x)-1) создается интерполяционный полином. Собственно, под созданием полинома здесь имеется в виду вычисление коэффициентов этого полинома. Коэффициенты записываются в переменную P. Командой z=-5.1:0.01:5.1 создаем список узловых точек, по которым будет строиться график интерполяционного полинома. Диапазон значений аргумента, для которого отображается график интерполяционного полинома, несколько шире диапазона, определяемого базовыми точками.Базовыеточкиотображаемкомандойplot(x,y,'ks'),акомандой plot(z,polyval(P,z),'r-') строим график интерполяционного полинома. Для сравнения, кроме интерполяционного полинома, выполняется еще

315

Самоучитель Matlab

и аппроксимация на основе полиномиального выражения. Коэффициенты соответствующего полинома вычисляются командой P2=polyfit(x,y,5). Аппроксимация выполняется на основе полинома пятой степени (третий аргумент функции polyfit()). Кривая на основе этого полинома отображается с помощью команды plot(z,polyval(P2,z),'k-.').

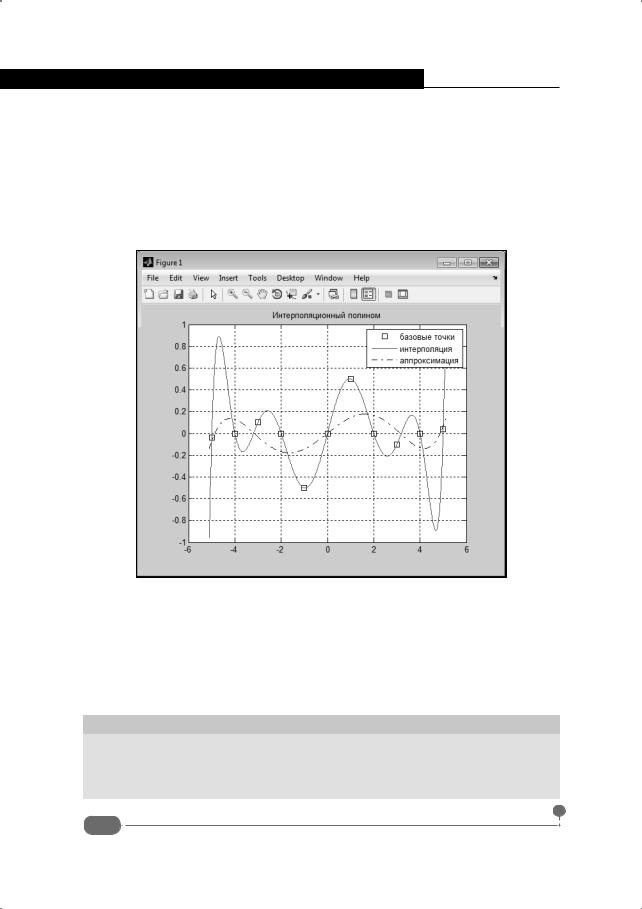
Заголовок добавляем командой title('Интерполяционный полином'), а легенду – командой legend('базовые точки','интерполяция', 'аппроксимация').Результат графических построенийпредставленна рис.8.4.

Рис. 8.4. Базовые точки, интерполяционный и аппроксимирующий полиномы

Интерполяционная кривая сплошная, а штрихпунктирная кривая соответствует полиномиальной аппроксимации. Что касается интерполяционного полинома, то по определению в узловых точках он дает табличные значения (те, на основе которых строится полином). Как отмечалось выше, в задаче аппроксимации такое условие не ставится. Достаточно, чтобы кривая проходила достаточно близко к базовым точкам. Что такое "достаточно близко" – вопрос отдельный.

На заметку

Каким бы способом ни строился интерполяционный полином, он один и тот же для фиксированного набора базовых точек. Другими словами, для данного набора базовых точек интерполяционный полином один. Как бы мы ни вычисляли этот полином, если вычисления правильные, получим один и тот же результат.

316

Глава 8. Обработка данных

При большом количестве базовых точек интерполяция полиномом может оказаться малопродуктивной. Одна из проблем связана с существенно немонотонным поведением полиномов высокой степени. Чтобы решить эту проблему, нередко используют интерполяцию сплайнами. Главная идея метода состоит в том, что диапазон интерполирования разбивается на поддиапазоны (например, в пределах между двумя соседними узловыми точками). В пределах каждого поддиапазона используются разные функции одного вида (полиномы невысокой степени). Эти функции "сшиваются" на границах поддиапазонов вместе с производными. В результате получаем кусочно-гладкую (вместе с производными нескольких первых порядков) интерполяционную зависимость.

Сплайн-интерполяцию в Matlab можно реализовать с помощью функции interp1(). Обычно аргументами функции interp1() передают набор узловых точек аргумента табулированной функции и значений функции в этих узловых точках. Это два списка, определяющие те базовые точки, на основе которых выполняется интерполяция. Третьим аргументом указывается список значений, для которых вычисляется значение интерполяционной зависимости. Этот аргумент может быть скаляром – тогда значение интерполяционной зависимости вычисляется в одной точке. Также четвертым аргументом можно указать (в одинарных кавычках) ключевое слово, определяющее тип базового сплайна (степень полинома). Для определения типа базового полинома используют следующие ключевые слова (табл. 8.1).

Табл. 8.1. Ключевые слова, определяющие тип базового полинома

Как правило, к интерполяции на основе базовых полиномов нулевой и первой степени на практике прибегают достаточно редко, поэтому рассмотрим методы интерполяции кубическими полиномами. Обратимся к рис. 8.5, на котором представлен документ с соответствующим примером.

317

Самоучитель Matlab

Рис. 8.5. Интерполяция кусочно-непрерывными функциями

Использована такая последовательность команд:

>>x=-1:0.2:1;

>>y=cos(3*pi*x);

>>z=-1:0.01:1;

>>f1=interp1(x,y,z,'spline');

>>f2=interp1(x,y,z,'pchip');

>>plot(x,y,'ks')

>>hold on

>>plot(z,f1,'r-','LineWidth',2)

>>plot(z,f2,'g--','LineWidth',2)

>>grid on

>>title('Интерполяция сплайнами')

>>legend('базовые точки','кубические сплайны','полиномы Эрмита')

В переменную x записываются узловые точки аргумента табулируемой функции. Значения табулируемой функции в узловых точках вычисляются командой y=cos(3*pi*x). В переменную z записываются значения аргумента, для которых необходимо вычислить интерполяционные зависимости. Интерполяционная зависимость на основе кубических сплайнов строится командой f1=interp1(x,y,z,'spline'). Здесь первые два аргумента (переменные x и y) задают базовые точки, на основе которых строится интерполяционная зависимость. Третий аргумент (переменная z) задает точки аргумента, для которых необходимо вычислить значения интерполяционной зависимости. Эти значения, как результат вызова функции interp1(), записываются в переменную f1. Опционный параметр 'spline' означает, что интерполяционная зависимость строится на основе базовых полиномов третьей степени. Аналогично, интерполяционная

318

Глава 8. Обработка данных

зависимость на основе полиномов Эрмита создается с помощью команды f2=interp1(x,y,z,'pchip').

На заметку

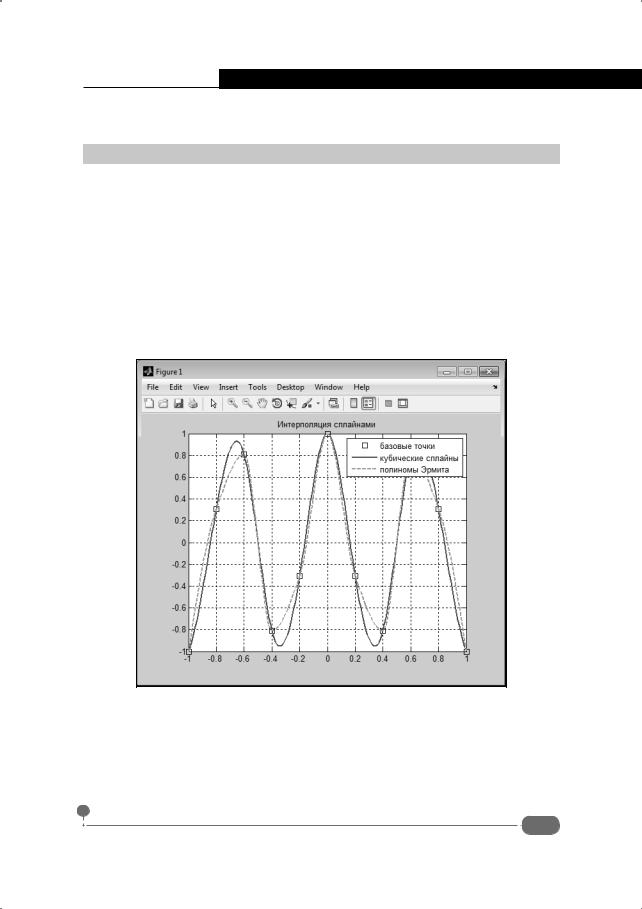
На рис. 8.6 показан результат интерполирования разными методами (обычными сплайнами и полиномами Эрмита) одной и той же табличной функции.

Рис. 8.6. Интерполяция кубическими сплайнами и полиномами Эрмита

Рассуждать вне контекста конкретной решаемой задачи о том, какой способ интерполирования лучше, особого смысла нет. Отметим лишь, каждый способ по-своему хорош.

319

Самоучитель Matlab

Аппроксимация

Это простейшая цепь рассуждений.

К/ф "Приключения Шерлока Холмса и доктора Ватсона. Знакомство"

Задача аппроксимации близка идеологически к задаче интерполяции, но все же это разные задачи. Например, предположим, что имеется набор узловых точек xk (индекс k = 1,2,...,n ) и значения некоторой функции yk в этих точках. Также есть известная функция f (x,a1,a2,...,am ), которая кроме аргумента x зависит еще и от некоторых параметров as (индекс s = 1,2,...,m ). Задача состоит в том, чтобы подобрать такие значения параметров as , что функция f (x,a1,a2,...,am ) наилучшим образом описывала бы зависимость, заданную параметрами xk и yk (индекс k = 1,2,...,n ). При этом количество m параметров as меньше (или даже намного меньше) количества узловых точек n . Поэтому добиться того, чтобы функция f (x,a1,a2,...,am ) давала "точные" значения yk в узловых точках xk , не удастся. Нужен критерий, который бы позволил определить, какая зависимость "лучше", а какая "хуже" аппроксимирует табличные значения. Обычно в качестве такого критерия используется принцип наибольшего правдоподобия, следствием которого является метод наименьших квадратов. В соответствии с этим методом параметры as (индекс s = 1,2,...,m )

n

выбираются так, чтобы сумма ∑(yk − f(xk,a1,a2,...,am ))2 принимала наи-

k =1

меньшее значение. Такая задача сводится к решению системы из m алгебраических уравнений – в общем случае нелинейных. Система решается относительно параметров as (индекс s = 1,2,...,m ). Эти уравнения име-

(для всех индексов s = 1,2,...,m ). В случае если функция f (x,a1,a2,...,am )

зависит от параметров as линейным образом, задача значительно упрощается и сводится к решению системы линейных уравнений. Действительно, в этом случае для функции f (x,a1,a2,...,am ) может быть использо-

320