1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 9. Символьные вычисления

Рис. 9.3. График функции, заданной на основе символьного выражения

Рис. 9.4. Замены в символьном выражении с несколькими переменными

351

Самоучитель Matlab

С вычислением значения такой своеобразной функции дела обстоят несколько хуже. Чтобы вычислить значение функции в точке, используем функцию subs(). Первым аргументом функции указывается переменная, определенная на основе символьного выражения. Второй аргумент – значение для символьной переменной. Это значение, кстати, тоже может быть символьным. В частности, командой subs(f,pi/2) вычисляется значение для числового аргумента, а командой subs(f,y) вычисляется выражение с заменой символьной переменной x на символьную переменную y.

Если в выражение входит несколько символьных переменных, то функцию subs() используют в немного ином формате. Первым аргументом, как и ранее, указывается переменная символьного выражения, а затем, через запятую, заменяемая в выражении символьная переменная и ее значение. На рис. 9.4 представлено продолжение предыдущего документа.

Команды здесь такие (жирным шрифтом выделен ввод пользователя):

>>z=cos(x*y)+x/y

z =

cos(x*y) + x/y

>>subs(z,x,1) ans =

cos(y) + 1/y

>>subs(z,y,x) ans =

cos(x^2) + 1

>>subs(subs(z,x,pi),y,0.5) ans =

6.2832

Командой z=cos(x*y)+x/y задается символьное выражение, в которое входят две символьные переменные x и y.

На заметку

Переменные x и y в качестве символьных объявлены ранее, в предыдущей части документа – см. рис. 9.3.

Результатом выполнения команды subs(z,x,1) является выражение, получающееся заменой в выражении z переменной x на 1. При этом выражение z не меняется. В результате выполнения команды subs(z,y,x) получаем выражение, которое получается из z заменой переменной y на x. Причем результат автоматически упрощается (насколько это возможно). Наконец, чтобы выполнить замену сразу нескольких символьных переменных, используем конструкцию из вложенных функций subs(), как в команде subs(subs(z,x,pi),y,0.5).

352

Глава 9. Символьные вычисления

Удобно то, что непосредственно в командном окне можно выполнять символьные операции и с числами. Для этого полезной станет функция sym(). Ее аргументом указывается (заключенное в одинарные кавычки) выражение, которое следует интерпретировать и обрабатывать как символьное. Таким символьным выражением может быть и число. Обратимся к примеру в документе, показанном на рис. 9.5.

Рис. 9.5. Символьные вычисления

Результатом команды sym('3/7')+sym('6/11') будет сумма дробей, причем вычисленная "точно", без округления. Результат представляется в виде правильной дроби. Далее, командой a=1+sqrt(sym('2')) опреде-

ляется переменная a с точным (символьным) значением 1 + 2 . Операции с этой переменной выполняются так, что их результат также вычисляется в символьном виде. Например, результат выражения a^2 символьный. Правда, он не очень компактный, но вызов команды simplify(a^2) упрощает соответствующее выражение.

На заметку

Для преобразования символьного числового выражения в формат числа с плавающей точкой используется функция vpa(). Ее аргументом указывают вычисляемое (преобразуемое) выражение. Второй необязательный аргумент определяет количество значащих цифр после десятичной запятой.

353

Самоучитель Matlab

Основные символьные операции

- Интересное решение. - Вы думаете?

- А что? Демократично, удобно.

- Честно говоря, мне виделось нечто более изящное.

К/ф "Чародеи"

В этом разделе кратко остановимся на некоторых задачах, которые часто приходится (или желательно) решать в символьном виде. К ним, безусловно, следует отнести дифференцирование, интегрирование, разложение функции в ряд Тейлора, а также решение дифференциальных и алгебраических уравнений. Для выполнения всех этих операций (а также многих других) в Matlab есть специальные встроенные функции, с которыми нам, собственно, и предстоит познакомиться. Начнем с дифференцирования.

Для вычисления производных (в том числе и частных) от символьных выражений используется функция diff(). У нее есть несколько форматов вызова. Самый простой случай – если необходимо вычислить производную от символьного выражения, в котором всего одна символьная переменная. В этом случае выражение указывается аргументом функции diff(). Этот и другие примеры вызова функции diff() представлены в документе на рис. 9.6.

Рис. 9.6. Вычисление производных

354

Глава 9. Символьные вычисления

Командой syms x y объявляются две символьные переменные x и y. Затем на основе этих переменных объявляем символьное выражение f=sin(x)/x. Для вычисления производной от этого выражения используем команду diff(f), в которой единственным аргументом функции diff() передано дифференцируемое выражение. Производная автоматически вычисляется по символьной переменной. Если переменных в выражении несколько, производная вычисляется по той, которая в алфавите "ближе" к букве x. Например, определим выражение F=sin(x)*y^2 и продифференцируем его с помощью команды diff(F). В данном случае производная вычисляется по переменной x. Чтобы вычислить производную по переменной y, используем команду diff(F,y). Здесь вторым аргументом явно указана переменная, по которой вычисляется производная.

Если вторым аргументом функции diff() указать целое число, то оно определит порядок производной от выражения, переданного первым аргументом функции. Обратимся к документу на рис. 9.7.

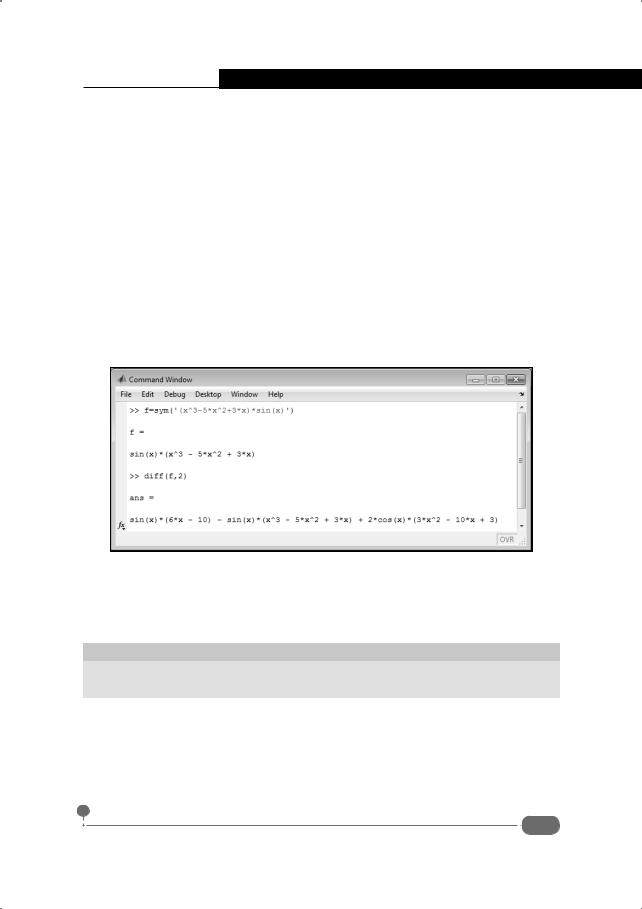
Рис. 9.7. Производная второго порядка

Здесь командой f=sym('(x^3-5*x^2+3*x)*sin(x)') определяется символьное выражение, в которое входит всего лишь одна символьная переменная x.

На заметку

Обратите внимание, как определяется символьное выражение: в одинарных кавычках оно указывается аргументом функции sym().

Вторую производную от созданного символьного выражения вычисляем с помощью команды diff(f,2). Можно также вызвать функцию diff() со следующим способом передачи аргументов: дифференцируемое выражение, переменная дифференцирования и порядок дифференцирования. Например, команда diff(f,x,2) означает вычисление второй производной от выражения f по переменной x.

355

Самоучитель Matlab

Обратной к дифференцированию является процедура интегрирования.

Вданном случае имеется в виду вычисление первообразной.

На заметку

Первообразной для функции f (x) называется такая функция F(x), производная от которой равняется f (x), то есть по определению F ′(x) = f (x). Задача вычисления неопределенного интеграла от функции (обозначается

∫ f(x)dx ) сводится к вычислению упомянутой выше функции F(x). Другими словами, если F(x) = ∫ f (x)dx , то это означает, что F ′(x) = f (x). Перво-

образная вычисляется с точностью до аддитивной постоянной, которую обычно для простоты не упоминают.

Для вычисления интеграла от символьного выражения используют функцию int(). Если единственным аргументом указано символьное выражение с одной символьной переменной, то в результате возвращается первообразная для выражения (если эту первообразную удается найти). Если в выражении несколько символьных переменных, интеграл вычисляется по переменной, наиболее близкой в алфавитном списке к букве x. Чтобы явно указать переменную интегрирования, ее передают вторым аргументом функции int(). Примеры приведены в документе на рис. 9.8.

Последовательность команд такая (жирным шрифтом выделен ввод пользователя):

>> f=sym('ln(x)') f =

log(x)

>>int(f) ans =

x*(log(x) - 1)

>>int('exp(a*x)*cos(b*x)') ans =

(exp(a*x)*(a*cos(b*x) + b*sin(b*x)))/(a^2 + b^2)

>>int('exp(a*x)',sym('a'))

ans = exp(a*x)/x

Сначала в переменную f записываем символьное выражение sym('ln(x)'). Затем командой int(f) вычисляем интеграл

356

Глава 9. Символьные вычисления

Рис. 9.8. Вычисление неопределенных интегралов

int('exp(a*x)*cos(b*x)'). В обоих случаях интегрирование по умолчанию выполняется по переменной x. Примером явного указания переменной интегрирования может быть команда int('exp(a*x)',sym('a')),

которой вычисляется интеграл ∫ exp(ax)da = exp(ax) по переменной a. x

Для вычисления определенных интегралов в символьном виде также используется функция int(). Только теперь она вызывается в несколько ином формате. Так, если переменная интегрирования определяется автоматически, то помимо подынтегрального выражения аргументами функции int() передаются пределы интегрирования – это второй и третий аргументы. Если вторым аргументом указать переменную интегрирования, то пределы интегрирования указываются третьим и четвертым аргументами.

На заметку

Напомним, что между определенным и неопределенным интегралами существует связь. Так, если имеет место соотношение ∫ f (x)dx = F(x),

357

Самоучитель Matlab

b

то определенный интеграл ∫ f(x)dx = F(b) −F(a). Обычно значение опре-

a

деленного интеграла отождествляют с площадью под графиком функции f (x) на интервале значений аргумента a ≤ x ≤ b .

В документе на рис. 9.9 приведены примеры вычисления определенных интегралов:

Рис. 9.9. Определенный интеграл

Рассмотрим команды подробнее (жирный шрифт означает ввод пользователя):

>>int('tan(z)',0,pi/4) ans =

log(2)/2

>>syms b positive

>>int('sin(b*x)/x',0,inf) ans =

pi/2

π4

Интеграл ∫ tg(z)dz = ln(2) вычисляется командой int('tan(z)',0,

2

0

pi/4). В данном случае первым аргументом функции int() передается интегрируемое символьное выражение (подынтегральная функция), а второй и третий аргументы – пределы интегрирования по символьной переменной z. Выбор на эту переменную пал в силу ее единственности в подынтегральном выражении.

Перед вычислением следующего интеграла мы используем команду syms b positive для того, чтобы объявить символьную переменную b

358

Глава 9. Символьные вычисления

и указать, что она положительная (ключевое слово positive в объявлении переменной) – эта информация важна при вычислении интеграла Дирихле

∞

∫sin(bx)dx = π . Интеграл вычисляем командой int('sin(b*x)/x',

x2

0

0,inf). Для обозначения бесконечности используем ключевое слово inf.

Еще одна достаточно часто встречающаяся на практике задача – разложение функции в степенной ряд (обычно ряд Тейлора).

На заметку

Рядом Тейлора для функции f (x) в окрестности точки a называется бесконеч-

∞

ная сумма f(x) = ∑cn(x −a)n . Коэффициенты разложения cn определя- n=0

ются на основе производных n -го порядка f (n)(a) функции f (x) в точке a ,

а именно: cn = f (n)(a) .

n !

Для вычисления ряда Тейлора функций (точнее, конечного количества слагаемых этого ряда) используют функцию taylor(). Первым аргументом функции указывается раскладываемое в ряд выражение. Далее может быть указана символьная переменная, по которой выполняется разложение. Если переменная не указана, она определяется автоматически по тем же критериям, что описывались выше для задачи интегрирования или дифференцирования. Следующий числовой аргумент определяет степень первого отбрасываемого слагаемого ряда (например, значение 10 этого аргумента означает, что в ряд будут вычислены слагаемые до 9 степени включительно). Также можно указать аргументом точку, в окрестности которой выполняется разложение в ряд. Если этот аргумент не указан, разложение выполняется в окрестности нуля. На рис. 9.10 приведены простые примеры разложений в ряд Тейлора.

пять слагаемых ряда Тейлора, а командой pretty(ans) вычисленный результат представляем в более-менее пристойном виде. Здесь мы для ссылки на результат выполнения предыдущей команды использовали ключевое слово ans.

359

Самоучитель Matlab

Рис. 9.10. Разложение в ряд Тейлора

На заметку

Команда taylor(f,10) означает, что при разложении выражения f в ряд учитываются слагаемые до 9 степени включительно. В сумме

пени 9 по переменной x отсутствует. Поэтому остаются слагаемые до 8-й степени включительно.

Следующей командой pretty(taylor(sym('ln(t)'),5,1)) выполняется разложение натурального логарифма ln(t) по переменной t в окрестности точки t = 1 до 4-й степени включительно. Результат сразу приводится к читабельному виду. Как несложно убедиться, в результате получаем

Кроме рассмотренных задач, хочется остановиться еще на двух – решении алгебраических и дифференциальных уравнений и систем. Начнем с алгебры.

Алгебраические уравнения и системы в символьном виде решаются с помощью функции solve(). Некоторые способы вызова этой функции для

360