1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 9. Символьные вычисления

Показательной в данном случае является команда solve(eq,x), которой решается квадратное уравнение общего вида (то есть ax2 +bx +c = 0 ). Предварительно это уравнение командой eq:=a*x^2+b*x+c=0 присваивается в качестве значения переменной eq. Обращаем внимание, что результат представлен для всех случаев: общий (если параметр a ≠ 0 ), решение линейного уравнения bx +c = 0 (при значении параметра a = 0 ), множество комплексных чисел (при всех нулевых значениях a = b = c = 0 решением уравнения является любое число) и пустое множество (при значениях параметров a = b = 0 и ненулевом параметре c ≠ 0 уравнение решений не имеет).

Для решения системы уравнений x2 + y2 = 25 и y −x = 1 используем команду solve([x^2+y^2=25,y-x=1],[x,y]). Здесь первым аргументом функции solve() передан список [x^2+y^2=25,y-x=1] с уравнениями решаемой системы, а второй аргумент – список [x,y] с переменными, относительно которых решается система.

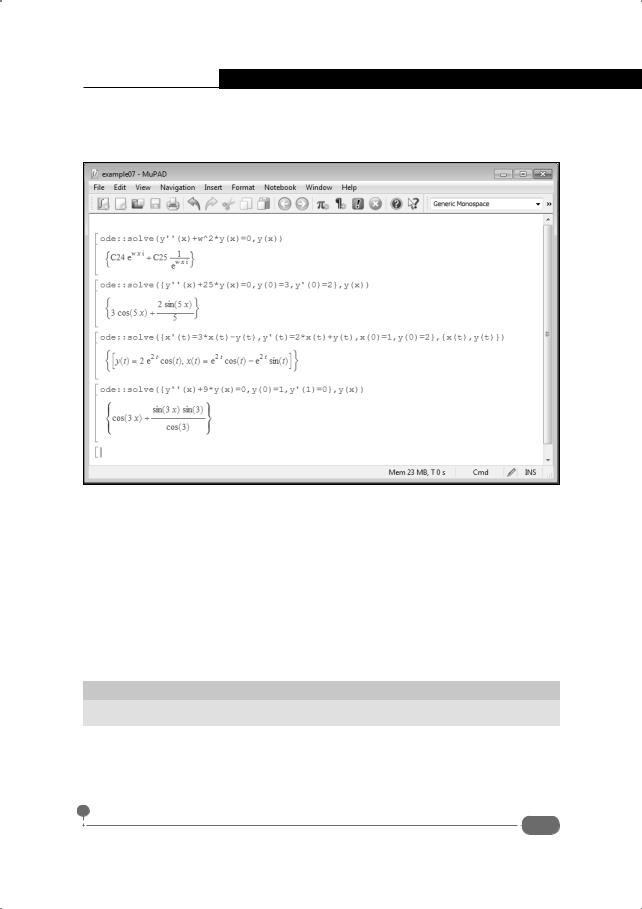
Точно так же обстоят дела с неравенствами. Некоторые простые примеры решения неравенств приведены в документе на рис. 9.30.

Рис. 9.30. Решение неравенств

Командой solve(x^2-5*x+6<0,x) предпринимаем попытку решить неравенство x2 − 5 + 6 < 0 . На множестве действительных чисел решение этого неравенства – диапазон значений аргумента от 2 до 3, то есть x (2, 3) . Этот диапазон отображается в области вывода результата. Тем не менее, кроме этого диапазона, там можно видеть что-то еще. Причина в том, что решение ищется на множестве комплексных чисел.

381

Самоучитель Matlab

На заметку

В качестве "дополнительного" решения указано множество вида 5 + iy , где

С одной стороны, это удобно. С другой стороны – ситуация существенно усложняется, а простые задачи нередко становятся сложными. Поэтому нередко приходится явно указывать, что решение ищется на каком-то множестве – обычно это множество действительных чисел. Например, чтобы найти решение неравенства на множестве действительных чисел, используем команду solve(x^2-5*x+6<0,x) assuming x in R_. От предыдущей команды она отличается инструкцией assuming x in R_. Состоит она из ключевого слова assuming и инструкции x in R_ - это инструкция в формате переменная in множество. Переменной в данном случае является x, а множеством, как отмечалось, является множество действительных чисел, что стандартно обозначается как R_.

Попытка решить неравенство на множестве действительных чисел приводит к ожидаемому результату. При решении более сложного полиномиального неравенства также разумно четко определить область поиска решений (команда solve(x^3-11*x^2+31*x-21<0,x) assuming x in R_). Получаем правильное решение для неравенства x3 −11x2 + 31x −21 < 0 , которое состоит в объединении интервалов x (−∞,1) (3, 7).

Решение дифференциальных уравнений

Все это так прямолинейно и перпендикулярно, что мне неприятно.

В. Черномырдин

Дифференциальные уравнения также можно решать функцией solve(). Правда, в этом случае необходимо приложить некоторые усилия – а именно, как-то намекнуть, что решается именно дифференциальное уравнение, а не какое-то другое. Существует несколько способов добиться этого. Но самый простой вариант, пожалуй, состоит в том, чтобы в явном виде указать метод поиска решения – для дифференциальных уравнений это ode

(сокращение от ordinary differential equation, то есть обыкновенное дифференциальное уравнение). Синтаксис вызова функции solve() имеет такой вид: ode::solve(). Первым аргументом указывается решаемое уравнение или заключенное в фигурные скобки множество уравнений (если решается

382

Глава 9. Символьные вычисления

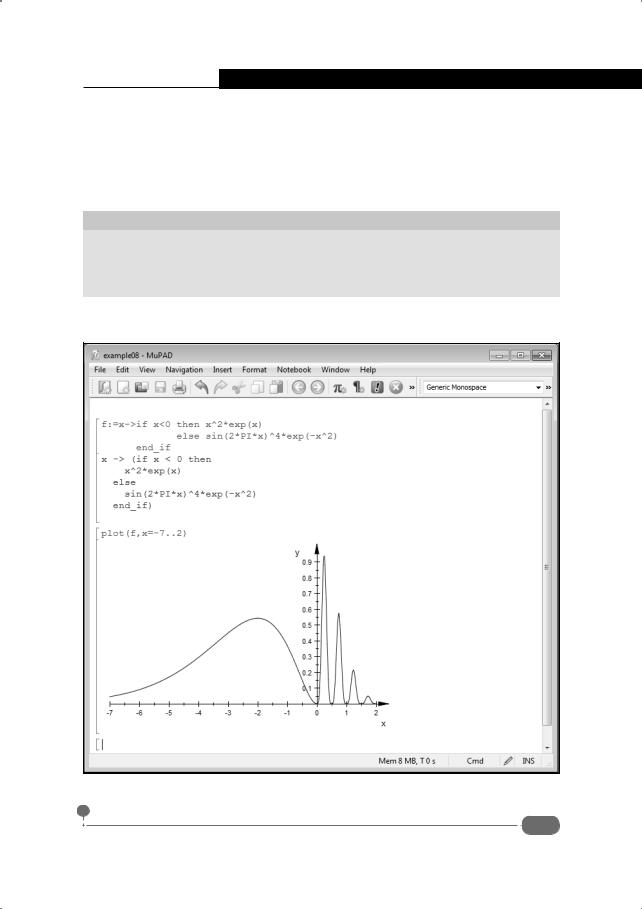
система). Также аргументами передается неизвестная функция (или функции – заключенные в фигурные скобки). Некоторые примеры решения дифференциальных уравнений приведены в документе на рис. 9.31.

Рис. 9.31. Решение дифференциальных уравнений

Документ содержит несколько примеров. Первый среди них – решение дифференциального уравнения y′′(x) + w2y(x) = 0 . Общее решение этого уравнения, как известно, представляет собой линейную комбинацию синуса и косинуса: y(x) = C1 cos(wx) +C2 sin(wx). Здесь через C1 и C2 представлены произвольные константы интегрирования, которые определяются из начальных или граничных условий. Если воспользоваться командой ode::solve(y''(x)+w^2*y(x)=0,y(x)), то фактически это решение и получим, правда, записанное в несколько ином виде – через комплексные экспоненты, то есть как y(x) = C1 exp(iwx) +C2 exp(−iwx) .

На заметку

Здесь имеет смысл напомнить формулу Эйлера exp(it) = cos(t) + i sin(t).

Далее командой ode::solve({y''(x)+25*y(x)=0,y(0)=3,y'(0)=2}, y(x)) решаем задачу Коши: уравнение y′′(x) + 25y(x) = 0 и начальные условия y(0) = 3 и y′(0) = 2 . Результат получаем точный и достаточно компактный.

383

Самоучитель Matlab

На заметку

Уравнение и начальные условия при передаче аргументом функции solve() заключаются в фигурные скобки.

По тому же принципу действуем, решая задачу Коши для системы дифференциальных уравнений x′(t) = 3x(t) −y(t), y′(t) = 2x(t) + y(t)

сначальными условиями x(0) = 1 и y(0) = 2 . Задача имеет решение x(t) = exp(2t)(cos(t) − sin(t)) и y(t) = 2 exp(2t)cos(t) . Соответствующая

команда выглядит как ode::solve({x'(t)=3*x(t)-y(t),y'(t)=2*x (t)+y(t),x(0)=1,y(0)=2},{x(t),y(t)}).

На заметку

В случае необходимости результат решения дифференциального уравнения или системы уравнений можно упрощать с помощью функции simplify()

или Simplify().

Задача с граничными условиями решается так же, как задача с начальными значениями,тольковместозначенияфункциииеепроизводныхвначальных точках задаются значения функции (и ее производных) в граничных точках. В качестве примера можно привести команду ode::solve({y''(x)+ 9*y(x)=0,y(0)=1,y'(1)=0},y(x)). С помощью этой команды решается уравнение y′′(x) + 9y(x) = 0 с граничными условиями y(0) = 1 и y′(1) = 0 . В результате найдено решение дифференциального уравнения, удовлетворяющее обоим граничным условиям.

Элементы программирования

Вопросы надо ставить уместно и своевременно.

К/ф "Чародеи"

Всреде MuPAD можно составлять программные коды, в которых вычисления выполняются в символьном виде. Здесь мы кратко рассмотрим основные управляющие инструкции, которые при этом допускается использовать.

ВMuPAD используется несколько базовых операторов. Для создания точек ветвления в программных кодах используется условный оператор if. Синтаксис его вызова следующий:

if условие then команды

else

команды end_if

384

Глава 9. Символьные вычисления

После ключевого слова if указывается условие, которое проверяется и в зависимости от истинности или ложности которого выполняется тот или иной блок команд. В частности, если условие истинно, выполняются команды, указанные после ключевого слова then. Если условие ложно, выполняются команды, указанные после ключевого слова else. Заканчивается условный оператор инструкцией end_if.

На заметку

Блок с инструкцией else не является обязательным. Если этот блок отсутствует, то условный оператор обрабатывается так: при истинном условии выполняются команды после ключевого слова then. Если условие ложно, управление передается следующему оператору, после условного.

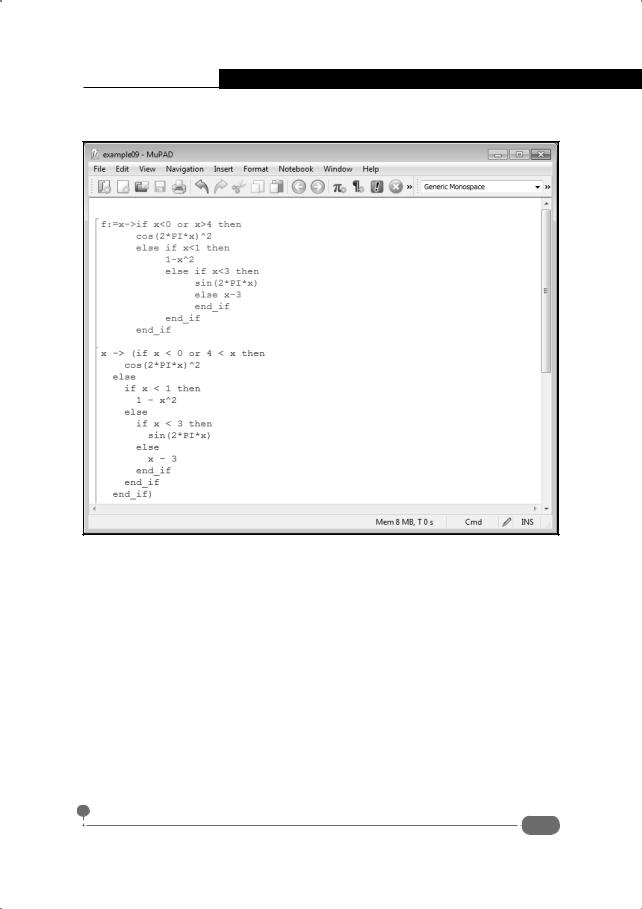
В документе на рис. 9.32 представлен код функции, в которой использован условный оператор.

Рис. 9.32. Использование условного оператора при определении функции

385

Самоучитель Matlab

Для объявления функции использован следующий программный код:

f:=x->if x<0 then x^2*exp(x)

else sin(2*PI*x)^4*exp(-x^2)

end_if

Всоответствиисэтимкодомопределяетсякусочно-непрерывнаяфункция,ко- торая при отрицательных аргументах принимает значение f(x) = x2 exp(x) и при неотрицательных аргументах равна f (x) = sin(2πx)4 exp(−x2) . Для большей наглядности там же приведен график описанной функции. График построен с помощью команды plot(f,x=-7..2). Здесь стоит обратить внимание, что первым аргументом указано только имя функции (без аргумента). Это необходимо, поскольку в противном случае, если указать аргумент, график построен не будет в силу невозможности обработать в символьном виде условие, проверяемое в условном операторе. В том формате вызова, который использован, оператор (имя функции), указанный первым аргументом функции plot(), действует на диапазон изменения переменной, указанной вторым аргументом функции plot().

Если проверяется несколько условий, используют вложенные условные операторы. Полезными могут стать и логические операторы, с помощью которых проверяются сложные условия.

На заметку

В MuPAD используются следующие логические операторы. Логическое и – оператор and, логическое или – оператор or, логическое исключающее или – оператор xor, логическое отрицание – оператор not, логическая импликация – оператор ==> и логическое тождество – оператор <=>. Результатом выражения A and B является значение TRUE, если оба операнда A и B равны TRUE. Если хотя бы один из операндов равен FALSE, результатом выражения является FALSE. Результатом выражения A or B является значение TRUE, если хотя бы один из операндов равен TRUE. Если оба операнда равны FALSE, значением выражения будет FALSE. Значение выражения A xor B равно TRUE, если один и только один из операндов равен TRUE (другой, соответственно, равен FALSE). Если оба операнда равны TRUE или оба равны FALSE, значением выражения A xor B будет FALSE. Выражение not A равняется TRUE, если операнд A равен FALSE. Если значение операнда A равно TRUE, результатом выражения является значение FALSE. Значение выражения A ==> B определяется как результат вычисления выражения (not A) or B, то есть результатом будет FALSE, если первый операнд равен TRUE, а второй операнд равен FALSE. Во всех прочих случаях результатом будет TRUE. Выражение A <=> B является эквивалентом выражения (A ==> B) and (B ==> A). Если проще, то результат выражения A <=> B равен TRUE при одинаковых значениях операндов и равен FALSE при разных значениях операндов.

Кроме того, для создания логических выражений часто используют операторы сравнения: равно (=), не равно (<>), меньше (<), больше (>), меньше или равно (<=), больше или равно (>=).

386

Глава 9. Символьные вычисления

Еще один пример объявления кусочно-непрерывной функции приведен в документе на рис. 9.33.

Рис. 9.33. Еще одна кусочно-непрерывная функция

Для определения функции использован следующий программный код:

f:=x->if x<0 or x>4 then cos(2*PI*x)^2

else if x<1 then 1-x^2

else if x<3 then sin(2*PI*x) else x-3 end_if

end_if end_if

В данном случае функция состоит из нескольких фрагментов. Для значений аргумента функции x < 0 и x > 4 соответствующая функциональная зависимость имеет вид f (x) = cos(2πx)2 . Для значений аргумента в диа-

387

Самоучитель Matlab

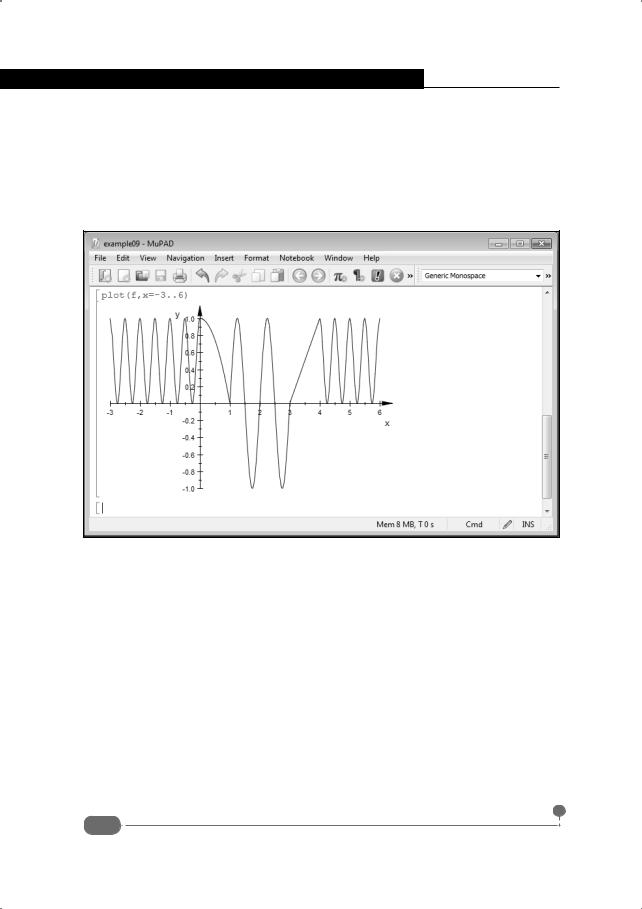
пазоне 0 ≤ x < 1 зависимость имеет вид f(x) = 1 −x2 . Для значений аргумента 1 ≤ x < 3 использована зависимость f (x) = sin(2πx). Наконец, в случае, если аргумент попадает в диапазон значений 3 ≤ x ≤ 4 , значение функции вычисляется по формуле f (x) = x − 4 . Весь этот нехитрый алгоритм реализован через систему вложенных условных операторов. Составить представление о том, как выглядит вся функциональная зависимость, можно по документу на рис. 9.34.

Рис. 9.34. График кусочно-непрерывной функции

Тот же программный код можно реализовать несколько проще (с точки зрения синтаксиса). В MuPAD во вложенных условных операторах вместо конструкции else if можно использовать одно ключевое слово elif. При этом соответствующий блок инструкцией end_if заканчивать не нужно. Другими словами, вместо синтаксической конструкции

if условие then команды

else if условие then

команды

else if условие then

команды

else команды

end_if

end_if

end_if

388

Глава 9. Символьные вычисления

используется конструкция вида

if условие then команды

elif условие then команды elif условие then команды else команды

end_if

Какая из них лучше в плане читабельности, решать читателю. Что касается нашей функции, то ее код мог бы выглядеть так (для удобства имя функции заменено на f2):

f2:=x->if x<0 or x>4 then cos(2*PI*x)^2 elif x<1 then 1-x^2

elif x<3 then sin(2*PI*x) else x-3

end_if

При этом результат выполнения команды определения функции фактически такой же, как и при использовании "неупрощенного" синтаксиса (рис. 9.35).

Рис. 9.35. Еще один способ определения кусочно-непрерывной функции

Желающие могут проверить, что это та же самая функция, что рассматривалась выше.

389

Самоучитель Matlab

Еще один способ проверки нескольких условий подразумевает использование оператора выбора case. В этом случае некоторое выражение проверяется на предмет совпадения с одним из возможных значений и в зависимости от того, есть совпадение или нет, выполняются определенные команды. Синтаксис вызова оператора такой:

case выражение of значение_1 do

команды_1

of значение_2 do

команды_2

...

otherwise

команды end_case

После ключевого слова case указывается проверяемое выражение. Далее идут блоки вида of значение do. Значение выражения, указанного после ключевого слова case, последовательно сравнивается со значениями в блоках of значение do до первого совпадения. Если совпадение найдено, выполняются все команды, начиная с соответствующего блока и до конца оператора case (инструкция end_case).

На заметку

Чтобы досрочно выйти из оператора выбора case, используют инструкцию break.

Необязательный блок с ключевым словом otherwise предназначен для случая, если при проверке выражения не найдено совпадений. Ниже приведен пример использования оператора выбора case для объявления функции, которая выводит текстовое сообщение в зависимости от переданного ей числового аргумента.

GetColor:=x-> case x

of 1 do

print(Unquoted,"1 - означает КРАСНЫЙ"); break

of 2 do

print(Unquoted,"2 - означает ЖЕЛТЫЙ"); break

of 3 do

print(Unquoted,"3 - означает ЗЕЛЕНЫЙ"); break

otherwise print(NoNL,x);

390