1-2 Моделирование / Matlab. Практический подход. Самоучитель

Глава 8. Обработка данных

Другими словами, по набору значений xk и yk (индекс k = 1,2,...,n ) нужно вычислить параметры a и b такие, чтобы зависимость f(x) = a exp(bx) наилучшим образом описывала эту зависимость. Пикантность ситуации в том, что функция f(x) = a exp(bx) нелинейным образом зависит от параметров a и b . Поэтому применяем военную хитрость и рассматриваем табулированную функцию со значениями zk = ln(yk ) в узловых точках xk (индекс k = 1,2,...,n ). Если исходная табулированная функция аппроксимируется зависимостью f(x) = a exp(bx), то новая функция записывается зависимостью F(x) = ln(f(x)) = ln(a) +bx , то есть зависимость линейная. Поэтому схема вычислений в данном случае такая:

•На основе табулированных значений xk и yk (индекс k = 1,2,...,n ) создаем новую табличную зависимость xk и zk = ln(yk ) (индекс

k= 1,2,...,n ).

•Для табличной зависимости xk и zk (индекс k = 1,2,...,n ) строим аппроксимирующую зависимость вида F(x) = c +bx . Находим коэффициенты b и c .

•Параметр a исходной модели связан с рассчитанным параметром c соотношением a = exp(c).

Пример вычислений, выполненных в соответствии с описанной схемой, приведен ниже (рис. 8.17).

Рис. 8.17. Нелинейная аппроксимация: простой случай

Командой x=0:10 создается набор узловых точек. Значения табулированной функции в узловых точках определяем командой

331

Самоучитель Matlab

y=3*exp(-0.2*x)+0.4*sin(pi*x/5). В данном случае использована функциональная зависимость y(x) = 3 exp(−0.2x) + 0.4 sin(πx 5) . Эта зависимость близка к экспоненциальной, но с некоторой поправкой (добавлен синус). Затем командой z=log(y) определяется новый набор точек. На основе этого набора командой p=polyfit(x,z,1) вычисляются коэффициенты аппроксимирующего полинома первой степени (линейная функция). Вычисленные коэффициенты записываются в список p. Элементы этого списка в команде a=[exp(p(2)) p(1)] используются для определения нового списка. В результате выполнения этой команды получаем следующий результат (ввод пользователя выделен жирным шрифтом):

>> a=[exp(p(2)) p(1)] a =

3.7148 -0.2795

Командой f=@(x)(a(1)*exp(a(2)*x)) определяем функциональную зависимость, на основе которой строится аппроксимирующее выражение. В этой зависимости использованы вычисленные на предыдущем шаге коэффициенты (список a). Прочий код предназначен для отображения базовых точек и аппроксимирующей кривой:

>>t=0:0.01:10;

>>plot(x,y,'rs','LineWidth',2)

>>hold on

>>grid on

>>plot(t,f(t),'b--','LineWidth',2)

Такого типа код использовался достаточно часто и особых комментариев, думается, не требует. Результат показан на рис. 8.18.

Можно полагать, что результат достаточно приемлемый. И получен он минимальными усилиями. Тем не менее, такой простой путь не всегда возможен.

В случае, если задачу к линейной свести не удастся, можно воспользоваться, например, встроенной функцией fminsearch(), предназначенной для поиска минимума функции нескольких переменных. Первым аргументом функции fminsearch() передается указатель на минимизируемую функцию, а также список начальных приближений для параметров этой функции. Поэтому общий подход может быть таким: если необходимо вычислить параметры ap (индекс p = 1,2,...,m ) функции f (x,a1,a2,...,am ) на

основе табличных значений (xk,yk ) (индекс k = 1,2,...,n ), то минимизиро-

n

вать будем функцию Φ(a1,a2,...,am ) = ∑(yk − f (xk,a1,a2,...,am ))2 по па-

k =1

раметрам a1,a2,...,am . Реализация этого подхода проиллюстрирована в следующем примере. Обратимся к документу, представленному на рис. 8.19.

332

Глава 8. Обработка данных

Рис. 8.18. Результат аппроксимирования исходной зависимости

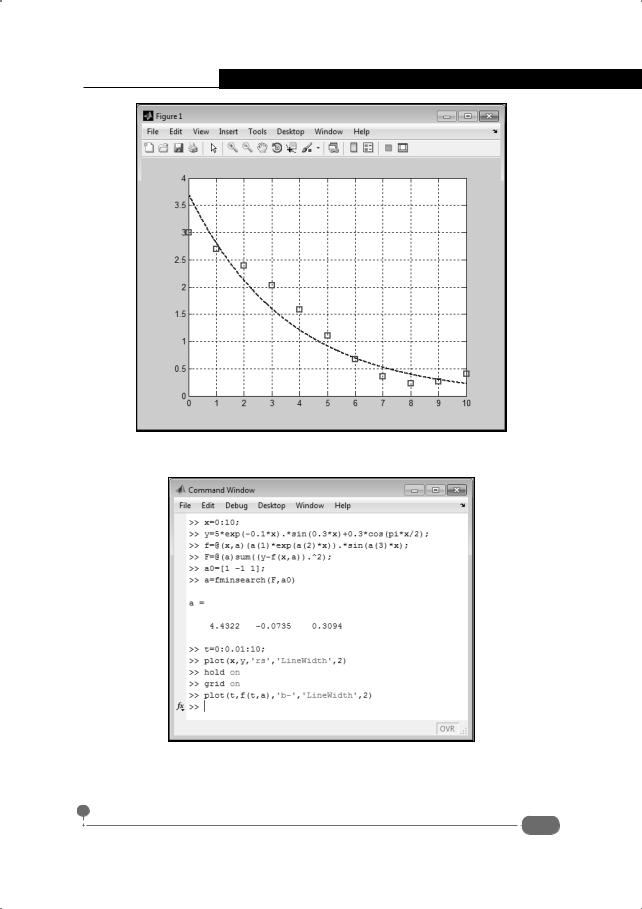
Рис. 8.19. Аппроксимация на основе нелинейной функции

333

Самоучитель Matlab

Весь командный код приведен ниже (жирным шрифтом выделен ввод пользователя):

>>x=0:10;

>>y=5*exp(-0.1*x).*sin(0.3*x)+0.3*cos(pi*x/2);

>>f=@(x,a)(a(1)*exp(a(2)*x)).*sin(a(3)*x);

>>F=@(a)sum((y-f(x,a)).^2);

>>a0=[1 -1 1];

>>a=fminsearch(F,a0)

a =

>>t=0:0.01:10;

>>plot(x,y,'rs','LineWidth',2)

>>hold on

>>grid on

>>plot(t,f(t,a),'b-','LineWidth',2)

На рис. 8.20 показан график с базовыми точками и аппроксимирующей кривой, построенной на их основе.

Рис. 8.20. Результат нелинейной аппроксимации

Теперь проанализируем командный код и полученный результат. Командами x=0:10 и y=5*exp(-0.1*x).*sin(0.3*x)+0.3*cos(pi*x/2)

создаются списки из базовых точек для создания на их основе ап-

334

Глава 8. Обработка данных

проксимирующей зависимости. При этом функциональная зависимость, которая использовалась для создания базовых точек, имеет вид y(x) = 5 exp(−0.1x)sin(0.3x) + 0.3 cos(πx 2). Командой f=@(x,a) (a(1)*exp(a(2)*x)).*sin(a(3)*x) создается функция, которая используется для создания аппроксимирующей зависимости. Мы используем

функцию f (x,a1,a2,a3) = a1 exp(a2x)sin(a3x). Параметры a1 , a2 и a3 необходимо найти. Для этого командой F=@(a)sum((y-f(x,a)).^2) создаем

функцию, которая зависит от искомых параметров и представляет собой сумму квадратов отклонений аппроксимирующей функции от табулированных значений в узловых точках. Эта функция должна принимать минимальное значение. Именно эту функцию будем минимизировать. Предварительно командой a0=[1 -1 1] создаем список начальных значений для искомых параметров модели. После этого вычисляем вектор параметров оптимизации командой a=fminsearch(F,a0). Прочие команды предназначены для отображения на графике базовых точек и аппроксимирующей кривой.

На заметку

Следует отметить, что полученный выше результат достаточно неплох как для нелинейной модели. Вообще же такие модели крайне сложны для анализа, поэтому всегда следует искать возможность для того, чтобы упростить ситуацию.

Генерирование случайных чисел

Я говорю об иных случайностях. Надеюсь, нам повезет, и мы встретим то, что единственное украшает жизнь, – настоящую неожиданность.

К/ф "Клуб самоубийц, или Приключения титулованной особы"

Достаточно важной с прикладной точки зрения является задача по генерированию случайных чисел. Обычно генерировать случайные числа приходится в процессе моделирования различных процессов. В любом случае, необходимость в генерировании случайных чисел возникает намного чаще, чем это может показаться на первый взгляд. Здесь мы рассмотрим самые простые приемы, которые не подразумевают использования специальных пакетов инструментов (благо, в Matlab недостатка в таких пакетах нет – например, пакет Statistics). Мы обойдемся несколькими функциями. В первую очередь это функция rand(), которая позволяет генерировать (псевдо)случайные равномерно распределенные действительные числа. У функции есть несколько вариантов вызова. Если вызвать функцию без аргументов (инструкция rand()), в качестве результата возвращается дей-

335

Самоучитель Matlab

ствительное число в диапазоне от 0 до 1. Если в качестве аргументов функции rand() указать целые числа, то в качестве результата возвращается массив соответствующих размеров, заполненный случайными действительными числами в диапазоне значений от 0 до 1. Например, в результате вызова команды rand(5,10) будет создана матрица размерами 5 на 10 из случайных чисел. Если указать один аргумент, например rand(5), то будет создана квадратная матрица соответствующего размера (в данном случае 5 на 5) из случайных чисел.

На заметку

Функция rand() далеко не единственная функция Matlab для генерирования случайных чисел. Например, функция randn() позволяет генерировать случайные числа с функцией стандартного нормального распределения, а функция randi() позволяет генерировать равномерно распределенные целые числа.

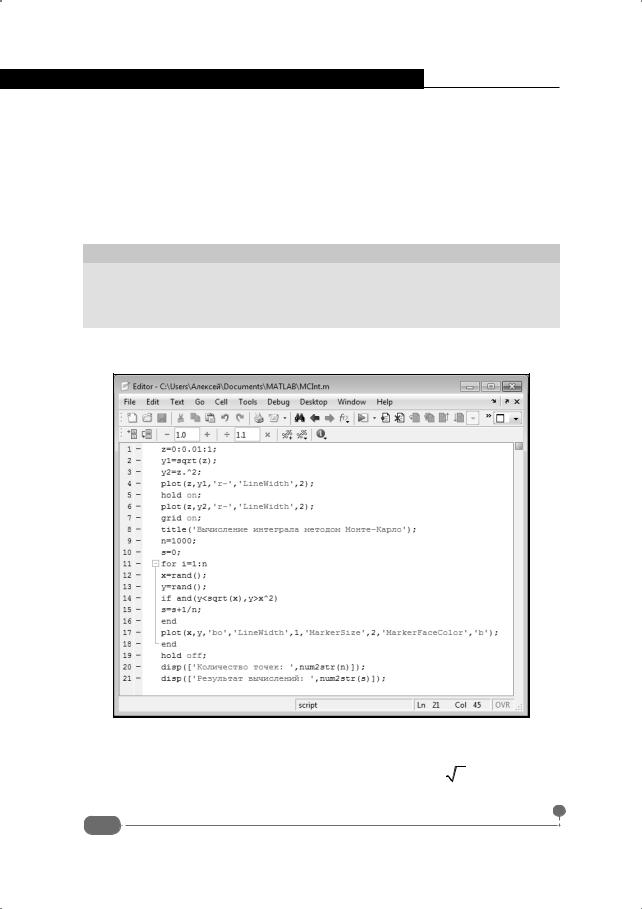
Простой пример использования функции генерирования случайных чисел приведен в документе на рис. 8.21.

Рис. 8.21. Вычисление площади области методом Монте-Карло

В качестве иллюстрации мы попытаемся методами Монте-Карло вычис-

336

грала дают одно и то же значение 1 3 .

На заметку

Если быть более точным, то двойной интеграл сводится к повторному, а повторный – к однократному. Тем не менее, с точки зрения идеологии метода МонтеКарло, правильнее было бы интерпретировать наши вычисления как расчет двойного интеграла (который равен площади соответствующе области). Что касается непосредственно метода Монте-Карло, то в данном случае он реализован по следующей схеме. В пределах единичного квадрата, внутри которого находится область, площадь которой мы вычисляем, случайным образом выбираются точки. Их много. Мы подсчитываем отношение количества точек, которые попали внутрь области, к общему количеству точек. В граничном пределе (когда количество точек неограниченно возрастает) это отношение стремится

котношению площадей области и площади квадрата (которая равна единице). Таким образом, чтобы вычислить площадь фигуры, нужно сгенерировать достаточно большое количество точек. Отношение количества точек внутри области

кобщему количеству точек принимаем как оценку для площади области.

Для выполнения вычислений создаем следующий программный код:

z=0:0.01:1;

y1=sqrt(z);

y2=z.^2; plot(z,y1,'r-','LineWidth',2); hold on; plot(z,y2,'r-','LineWidth',2); grid on;

title('Вычисление интеграла методом Монте-Карло'); n=1000;

s=0;

for i=1:n x=rand(); y=rand();

if and(y<sqrt(x),y>x^2) s=s+1/n;

end plot(x,y,'bo','LineWidth',1,'MarkerSize',2,'MarkerFaceColor','b'); end

hold off;

disp(['Количество точек: ',num2str(n)]); disp(['Результат вычислений: ',num2str(s)]);

337

Самоучитель Matlab

Вместе с вычислением площади области мы также выполняем некоторые графические построения. Вначале создается график с кривыми для зависимостей, которые ограничивают область. После этого командой n=1000 задаем количество точек, которые будут сгенерированы. В переменную s, которая инициализируется с начальным нулевым значением, будем записывать результаты вычислений площади. Вычисления выполняются в операторе цикла. Индексная переменная пробегает значения от 1 до n. Командами x=rand() и y=rand() генерируются случайные числа, которые служат координатами случайной точки. Затем в условном операторе проверяется условие and(y<sqrt(x),y>x^2), которое означает, что точка попадает внутрь области. Если это так, командой s=s+1/n увеличиваем значение переменной s. Но это еще не все. Сгенерированную точку мы отображаем на графике с помощью команды plot(x,y,'bo','LineWidth',1, 'MarkerSize',2,'MarkerFaceColor','b'). Точки отображаются синими кружками с синей заливкой маркера (опция MarkerFaceColor). В завершение кода выводится информация о количестве сгенерированных точек и оценке для площади области. В этом случае мы использовали команду disp(). Аргументом передается текстовая строка. Строка получается созданием массива с текстовыми элементами. Для перевода числа в текстовый формат использовалась функция num2str().

На заметку

Для объединения строк можно было бы использовать и функцию strcat(). Однако эта функция автоматически удаляет конечные пробелы в объединяемых строках, что в данном случае не очень приемлемо.

Приведенный выше код сохраняем в файле MCInt.m. После этого для выполнения комплекса вычислений в командном окне выполняем команду MCInt (рис. 8.22).

Рис. 8.22. Вычисление интеграла в командном окне

Здесь мы реализуем вычисления на основе 1000 точек. Это не очень много, поэтому результат от запуска к запуску может существенно меняться (на уровне сотых). График с точками, который создается в результате выполнения кода, представлен на рис. 8.23.

338

Глава 8. Обработка данных

Рис. 8.23. Графическое представление результата

На заметку

Даже из этого простого примера видно, что точность метода Монте-Карло оставляет желать лучшего. Чтобы добиться приемлемого результата, необходимо существенно увеличить количество тестов. А это требует значительных затрат времени (и ресурсов). Поэтому к методам вроде Монте-Карло обычно прибегают, когда другие методы неприменимы.

Выше мы рассматривали задачу, в которой нужно было генерировать случайные числа, равномерно распределенные в диапазоне от 0 до 1. На практике приходится иметь дело со случайными величинами, которые имеют самые разные законы распределения. В таких случаях можно либо воспользоваться встроенной функцией (если такая есть) для генерирования чисел с нужными характеристиками, либо создать собственную. Нас интересует последний случай. Пикантность ситуации состоит в том, что создать функцию, генерирующую случайные числа с практически любой приличной (не очень экзотической) функцией распределения, можно на основе функции, генерирующей равномерно распределенные числа. Другими словами, на основе функции rand() можно достаточно просто создать функцию, которая генерирует числа с заданным законом распределения.

339

Самоучитель Matlab

Полезным окажется то обстоятельство, что если случайная величина ξ распределена на интервале [0,1], то случайная величина η = F−1(ξ) имеет функцию распределения F(x). Здесь функция F(x) непрерывная и строго возрастающая, а через F−1(x) обозначена обратная функция к функции F(x). Таким образом, если нам нужно создать функцию для генерирования случайных чисел с функцией распределения F(x), то мы должны найти обратную функцию F−1(x), а затем вычислять случайные числа η в соответствии с соотношением η = F−1(ξ), где случайное число ξ генерируется, например, с помощью функции rand().

На заметку

Напомним, что по определению функцией распределения Fξ(x) случайной величины ξ называется вероятность P(ξ < x) того, что случайная величина принимает значение меньшее x (параметр −∞ < x < +∞). Плотностью

распределения случайной величины называется функция pξ(x) = dFξ(x) .

dx

Для равномерно распределенной на интервале от 0 до 1 случайной величины функция распределения имеет вид Fξ(x) = 0 при x < 0, Fξ(x) = x при

0 ≤ x ≤ 1 и Fξ(x) = 1 при x > 1. Плотность распределения для этого распределения pξ(x) = 1 при x [0,1] и pξ(x) = 0 при x [0,1].

В качестве примера применения на практике описанного выше принципа создадим функцию, которая позволит генерировать случайные числа с показательным распределением.

На заметку

Случайная величина ξ распределена с показательным законом с параметром

α, если функция ее распределения равна Fξ(x) = 1 − exp(−αx) при x ≥ 0

иравна нулю в противном случае (то есть при x < 0).

Вданном случае функция распределения F(x) = 1 − exp(−αx). Обрат-

ная к ней функция может быть найдена в результате решения уравнения x = F(y) относительно y , то есть y = F−1(x) . Это нам позволит найти обратную функцию. Имеем y = 1 − exp(−αx) . После несложных преобразо-

этому если мы будем генерировать случайные числа ξ функцией rand(),

ηбудут иметь показательное распределение с параметром α . Обратимся

кдокументу на рис. 8.24.

340