
method_eltech_v3.2.53_2013-11-17
.pdf
A C E
A |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
J |
E3 E4 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
R2 |
|
|
R3 |
|
|
|
|
|
|
R2 |
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
R3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
C |
= |
|
|
E3 E4 |
|
E4 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
R |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
R2 |
|
|
|
R3 |
|
R2 |
|
R3 |
|
|
|
R5 |
|
|
|
R6 |
|
R8 |
|
|
|
R8 |
|
|
|
|
|
|
3 |
|
|
|
|
5 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
E |
|
|
|
J1 |
|
|
E7 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R8 |
|
|
|
|
|
|
|
|
|
|
R7 |
R8 |
|
|
|
|
|
|
|
|
R7 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Решение |
данной |
|
матрицы |
даёт |
потенциалы |
|
узлов |
A, C и |
E. |
|||||||||||||||||||||||||||||||||||||||
Для нахождения токов всех ветвей мы должны вернуться к исходной схеме
Ошибка! Источник ссылки не найден., а, где дополнительно находим |
|||||||
значения потенциала узла B: B C E4 . |
|
||||||
|
4) Нахождение токов ветвей производится по закону Ома: |
|
|||||
I6 |
I1 J1 |
; |
I2 |
A C |
R2 ; |
I3 E E3 A R3 ; |
I5 B R5 ; |
C R6 |
; I7 |
|
E7 E R7 |
; I8 |
E C R8 . |
|
|
|
Ток особой ветви 4 определяется по закону Кирхгофа: |
|
|||||
|
I4 I3 |
I5 |
или I4 I2 I8 I6 . ■ |
|
|||
4.7 Метод контурных токов
Метод контурных токов также используется для составления системы уравнений, описывающих схему, с сокращённым числом неизвестных.
[Начать с примера, затем перейти к общим формулам.] Предположим, что в схеме выбрано необходимое количество незави-
симых контуров. В этом методе вводится следующая абстракция: представляется, что по каждому из этих контуров течёт свой особый контурный ток, неизменный вдоль всего контура; при этом реальный ток каждой ветви равен алгебраической сумме контурных токов, проходящих через данную ветвь (контурных токов всех контуров, включающих данную ветвь).
Контурные токи, проходя через любой узел, по определению остаются неизменными, следовательно, первый закон Кирхгофа выполняется автоматически. Поэтому уравнения составляются только по второму закону. Число уравнений по МКТ равно числу уравнений по ЗНК (равно числу главных контуров)
NМКТ = NВ – NУ + 1, |
(4.58) |
где NВ — число ветвей схемы, NУ — число узлов схемы. 71

В случае, если ищутся только токи ветвей, то количество уравнений уменьшается на количество особых ветвей с источниками тока (NJ):
NМКТ = NВ – NУ + 1 – NJ. |
(4.59) |
В случае, если источник тока входит в несколько выбранных контуров, необходимо один из них оставить, а вместо остальных выбрать другие контуры, не содержащие источников тока.
1)На первом шаге расчёта выбирается необходимое количество независимых контуров. В качестве таких контуров можно использовать набор главных контуров графа схемы или контуры, образуемые ячейками.
2)Далее для всех выбранных контуров, за исключением контуров
сизвестными контурными токами, составляется система уравнений по второму закону Кирхгофа, включающая в качестве неизвестных контурные токи. Пусть m — общее количество независимых контуров, из которых n имеют неизвестные контурные токи, а токи остальных m n контуров известны. Общий вид системы уравнений показан в (4.60), а её матричеая форма записи в (4.61), где
IКi ,i 1,n — неизвестный контурный ток контура i ; IКx , x n 1,m — известный контурный ток контура x ;
контураRii i,i; 1,n (с одинаковыми индексами) — контурное сопротивление
Rij ,i 1,n, j 1,m (с разными индексами) — межконтурное сопротивление контуров i и j ;
EКi ,i 1,n — контурная э. д. с. контура i .
Сопротивление Rii равно сумме сопротивлений вдоль контура i . Все Rii берутся со знаком «+».
Сопротивление Rij равно сумме сопротивлений ветвей, общих для контуров i и j , взятых со знаком «–», если токи контуров i и j в общей ветви направлены противоположно. По определению, Rij Rji .
Контурная э. д. с. EКi представляет собой полную сумму э. д. с. вдоль контура от действительных и эквивалентных источников э. д. с., взятых со знаком «–», если они действуют против направления контурного тока, т. е. направления обхода.
I |
К1R11 |
I |
К2R12 |
IКnR1n |
IК,n 1R1,n 1 |
IКmR1m |
EК1 |
|
||||||
|
|
|
|
|
|
|||||||||
падение напряжения под действием |
падение напряжения под действием |
|
|
|||||||||||
|
|
неизвестных контурных токов |
|
известных контурных токов |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.60) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IК1R21 IК2R22 IКnR2n IК,n 1R2,n 1 IКmR2m EК2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
R |
I |
R |
I |
R |
I |
К,n 1 |
R |
I |
R |
E |
Кn |
|
|
|
|
К1 n1 |
|
К2 n2 |
|
Кn nn |
|
n,n 1 |
|
Кm nm |
|
|
||
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|

индексы |
|
|
|
|
|
|
|
|
|
контуров: |
1 |
2 |
n |
|
|
|
|
|
|
1 |
R11 |
R12 |
|
R1n |
|
IК1 |
|
EК1 IК,n 1R1,n 1 |
|
|
|
IКmR1m |
|
||||||
|
|
|
|
|
|
|
|
|
|
2 |
R21 |
R22 |
|
R2n |
|
IК2 |
= |
EК2 IК,n 1R2,n 1 |
(4.61) |
IКmR2m |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
Rn1 |
Rn2 |
|
Rnn |
|
IКn |
|
EКn IК,n 1Rn,n 1 |
|
|
|
IКmRnm |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RijIКj = EКj |
|
|
||
Слева в системе (4.61) стоит квадратная матрица коэффициентов — контурных и межконтурных сопротивлений (размерности n n ), которая умножается на столбец неизвестных контурных токов (размерности n ). Справа стоит столбец свободных членов – контурных э. д. с. (размерности n ); также в правую часть с обратным знаком перенесены произведения известных контурных токов на межконтурные сопротивления с данным контуром.
Контурные сопротивления Rii ,i 1,n занимают главную диагональ, межконтурные сопротивления Rij ,i 1,n, j 1,m находятся вне главной диагонали.
3)Решение системы уравнений (4.61) проводится либо вручную (приведением к диагональному виду или использованием определителей и др.), либо с помощью математической компьютерной программы. Напри-
мер, в программе MathCAD решение линейного матричного уравнения можно произвести в виде произведения R 1E , дающего столбец неизвестных.
4)После нахождения контурных токов определяются токи ветвей путём алгебраического сложения всех контурных токов, протекающих через соответствующие ветви.
□ Пример 11. Рассмотрим пример расчёта схемы рис. 4.24, а по методу контурный токов.
1)Независимые контуры можно выбрать формальным методом, как показано на рис. 4.24, а или с помощью ячеек, как показано на рис. 4.24, б. Расчёт будем вести формальным методом, на основе главных контуров. На рис. 4.24, а очень жирной линией показано выбранное дерево. В этой схеме
73
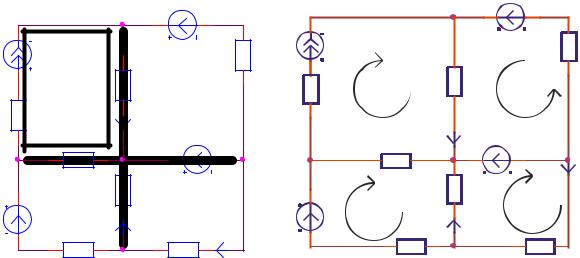
будет 4 главных контура К1, К3 , К5 , К7 , определяемых ветвями связи 1, 3, 5, 7, со своими контурными токами IК1 , IК3 , IК5 , IК7 , IК7 (показаны на рис. 4.24, б). Направления главных контуров (это и есть направления обхода) при использовании формального метода определяются направлениями самих контуров, т. е. их ветвей связи, а иначе произвольно.
2) Ток первого контура известен и равен IК1 J1 , для него не составляется уравнение, а для остальных В–У+1–1=8–5+1–1=3 контуров с неизвестными контурными токами уравнения составляются. Для учёта влияния контурного тока IК1 на распределение напряжений остальных контуров необходимо в каждое уравнение включить прозведения известных контурных токов на межконтурные сопротивления с данным контуром.
Соответствующие уравнения выглядят следующим образом:
IК3IК5IК5
R2 R3 E3 E4 J1R2
R5 R6 IК7R6 E4
R6 IК7 R6 R7 R8 E7 J1R8
Ниже приведена запись этих уравнений в матричной форме:
|
|
A |
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E3 |
|
J1 |
|
|
|
E3 |
|
|
J1 |
|
R3 |
|
|
|
R3 |
|
||
|
|
|
|
|
|
|
|
|||
|
R2 |
|
|
|
|
R2 |
|
|
||
|
|
|
|
R1 |
Iк1 |
|
Iк3 |
|
||
|
R1 |
|
|
|
|
|
|
|
||
|
I2 |
|
|
|
|
|
|
|
|
|
|
|
E4 |
|
|
R8 |
|
I |
|
|
|
|
|
C |
|
B |
E |
|
C 2 |
E4 |
B |
|
E |
|
|
|
|
||||||
R8 |
|
|
|
|
|
|
|
I5 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
R6 |
|
|
|
|
|
R6 |
|
|
|
E7 |
|
|
E7 |
Iк7 |
|
Iк5 |
|
||
|
|
|
|
R7 |
DI6 |
|
||||
|
R7 |
DI6 |
R5 |
I5 |
|
|
R5 |
|
(а) |
(б) |
Рис. 4.24. Схема с источником тока, жирной линией отмечен контур 1, очень жирной дерево (а), схема, на которой показаны контуры (б)
74

индексы |
|
|
|
|
|
|
|
контуров: |
3 |
5 |
7 |
|
|
|
|
3 |
R2 R3 |
|
|
|
IК3 |
|
E3 E4 J1R2 |
5 |
|
R5 R6 |
R6 |
|
IК5 |
= |
E4 |
7 |
|
R6 |
R6 R7 R8 |
|
IК7 |
|
E7 J1R8 |
Решением этой системы будет столбец неизвестных контурных токов
IК3 , IК5 , IК7 .
3) После нахождения всех контурных токов мы можем найти реаль-
ные токи ветвей: I1 J1 , I2 IК3 J1, I3 IК3 , I4 IК3 IК5 , I5 IК5 ,
I6 IК5 IК7 , I7 IК7 , I8 IК7 J1. ■
75
5 Электрические цепи синусоидального сигнала
Equation Section (Next)
5.1. Основные понятия. — 5.2. Комплексный (символический) метод записи электрических сигналов. — 5.3. Анализ цепи по синусоидальному сигналу. — 5.4. Резонанс в электрических цепях.
5.1 Основные понятия
Переменным называется сигнал (ток или |
напряжение), величина |
и направление которого меняется во времени: |
i f t . Периодическим |
называется такой переменный сигнал, значение которого повторяется в одной и той же последовательности через равные промежутки времени, называемые периодами: i t i t T , где T — период переменного сигнала. Величина, обратная периоду, называется частотой, измеряется в герцах (Гц): f 1 T , её смысл – количество периодов в секунду. Промышленная частота в России и Европе 50 Гц, в США 60 Гц.
T , её смысл – количество периодов в секунду. Промышленная частота в России и Европе 50 Гц, в США 60 Гц.
Переменный ток получил широкое распространение благодаря применению трансформаторов, позволяющих с минимальными потерями преобразовывать амплитуду переменного сигнала, а значит передавать электроэнергию на большие расстояния по длинным линиям с высоким напряжением и малым током с меньшими потерями, а затем распределять её между потребителями с низким напряжением и большим током.
Наиболее распространёнными и самыми простыми из переменных
сигналов являются синусоидальные (гармонические), |
представляемые |
в форме (см. рис. 5.1): |
|
i Im sin t i |
(5.1) |
( а ) ( б ) ( в )
Рис. 5.1. Синусоидальный сигнал с нулевой (а), положительной (б) и отрицательной (в) начальной фазой
Здесь, как более удобная, используется круговая частота 2 f , измеряемая в радианах в секунду, f 50 Гц соответствует 314,16 с-1; аргумент синуса называется фазой, при t 0 получается начальная фазаi . Начальная фаза определяет величину сигнала в начальный момент
76
времени и может быть положительной, отрицательной или нулевой. Она отсчитывается от начала синусоиды до оси ординат; началом синусоиды считается точка перехода от отрицательной полуволны к положительной.
В соответствии с правилами преобразования Фурье, любую периодическую функцию можно представить в виде ряда, содержащего постоянную составляющую и ряд гармоник (синусоид) с частотами, кратными основной:
|
|
i Im0 Imk sin k t k . |
(5.2) |
k 1
Это равносильно наложению (суперпозиции) отдельных гармонических источников, реакцию каждого их которых можно в первом приближении рассматривать как независимую от других. Если в схеме действуют источники разной частоты, в том числе составляющие периодической функции, то на каждой из этих частот схема рассчитывается отдельно, а результаты затем складываются.
По традиции, мгновенные составляющие токов, напряжений и других величин обозначают строчными буквами: i , u …, амплитуды сигналов
обозначают заглавными буквами с индексом m : Im , Um …
Разность фаз 1 2 двух синусоидальных сигналов называется углом сдвига. При 0 ( 1 2 ) говорят, что сигналы совпадают по фазе, при сигналы находятся в противофазе, при 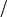 2 в квадратуре. Если 0 , то говорят, что первый сигнал опережает второй сигнал по фазе, если 0, то отстаёт по фазе.
2 в квадратуре. Если 0 , то говорят, что первый сигнал опережает второй сигнал по фазе, если 0, то отстаёт по фазе.
5.1.1 Действующее (эффективное) значение
Действующим (эффективным) значением силы переменного тока
(напряжения) называется его среднеквадратическое значение. Физический смысл этой величины следующий – это такое значение постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода.
Для того, чтобы вычислить это значение, представим два одинаковых резистора с номиналом R ; через первый течёт постоянный ток I , а через второй — переменный ток i с амплитудой Im . И пусть токи подобраны так, что мощность, которая выделяется в обоих резисторах за время полного периода T , одинакова.
Воспользуемся законом Джоуля–Ленца:
I 2RT T i2Rdt , |
(5.3) |
0
77

где выражение в левой части выражает количество энергии, выделяемой за время периода в резисторе величиной R постоянным током величиной I ; выражение в правой части выражает количество энергии, выделяемой за время периода в резисторе R переменным током i . Отсюда действующее значение I переменного тока равно его среднеквадратическому значению:
|
1 |
T |
2 |
|
|
Im |
|
I |
|
i |
|
dt (для синусоидального тока) |
|
(5.4) |
|
T |
|
2 |
|||||
|
|
0 |
|
|
|
|
|
Аналогично действующим значением синусоидального напряжения |
|||||||
u с амплитудой Um называется величина U Um |
2 . |
|
|
||||
Таким образом, |
|
действующее значение это постоянная величина, |
|||||
характеризующая данный переменный сигнал. Большинство измерительных приборов показывают именно действующие значения измеряемых переменных сигналов. При расчёт переменных сигналов также в большинстве случаев используется эта характеристика, а не амплитуда. В случае синусоидального сигнала принципиальной разницы нет: между амплитудой и действующим значением элементарная связь. Но для более сложных переменных сигналов действующее значение несомненно является важным показателем.
5.1.2Особенности записи топологических уравнений при расчёте по синусоидальному сигналу
При расчёте схемы по синусоидальному сигналу используются уже известные из первой части курса принципы, законы и методы (законы Кирхгофа, МУП, МКТ и т. п.), за одним исключением: все сигналы синусоидальные и связи между токами и напряжениями элементов выражаются компонентными уравнениями (1.5), (1.8), (1.11).
Рассмотрим простейшее последовательное соединение двухполюсников, подключённое к внешнему источнику э. д. с. с напряжением u :
R L C
A B
Рис. 5.2. Последовательная R-L-C-цепь
Запишем для этого участка схемы закон Ома (с использованием ком-
понентных уравнений (1.5), (1.8), (1.11)):
u u |
R |
u |
L |
u |
iR L di |
|
1 |
idt |
(5.5) |
|
|||||||||
|
|
C |
dt |
|
C |
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
78 |
|
|
|
|
При использовании таких выражений в топологических уравнениях получаются интегрально-дифференциальные уравнения, решение которых во многих реальных случаях возможно только в численном виде.
5.2 Компле́ксный (символический) метод записи сигналов
За исключением простейших случаев, запись и анализ уравнений, описывающих схему при воздействии синусоидального сигнала, удобнее производить в алгебраическом виде с использованием комплексного (символического) метода записи, в котором сигналы записываются в форме комплексных чисел.
5.2.1 Операции с комплексными числами
(Все операции иллюстрировать на комплексной плоскости). Комплексное число это двумерное число, или упорядоченное множе-
ство двух обычных действительных чисел. Оно записывается в видеA, B , где первый элемент A называется действительной частью, а второй элемент B мнимой частью комплексного числа. Комплексное число можно представить в виде точки на двумерной комплексной плоскости, где по горизонтальной оси откладывается действительная часть A , а по вертикальной оси мнимая часть B . В этом случае декартовы координаты точки будут A, B , причём каждая точка плоскости однозначно соответствует какому-либо числу; для указания точки на комплексной плоскости также
можно использовать полярные координаты: длину |
Fm радиус-вектора |
||||
к данной точке и угол его наклона к горизонтальной оси (см. рис. 5.3). |
|||||
Связь между декартовыми и полярными координатами точки: |
|||||
F |
A2 B2 |
arctg |
B |
|
|
|
|
||||
m |
|
|
A |
(5.6) |
|
|
|
|
|||
A Fm cos |
B Fm sin |
|
|||
Рис. 5.3. Комплексное число A, B на комплексной плоскости A — действительная часть, B – мнимая часть,
Fm — амплитуда, — аргумент
79
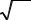
Для операций с комплексными числами используют две формы за-
писи комплексного числа, соответствующие декартовым и полярным ко- |
||||||
ординатам: алгебраическую A jB |
и |
показательную Fme j . |
Здесь |
|||
j |
1 – мнимая единица. |
|
|
|
|
|
|
Операции с мнимой единицей (иллюстрируются на комплексной |
|||||
плоскости): |
|
|
|
|
|
|
|
|
e j j2 1 e j |
3 |
|
1 j |
|
|
e j 2 j |
2 |
j3 j |
(5.7) |
||
|
|
|
|
|
j |
|
Пример суммы, произведения и деления двух комплексных чиселA, B и C, D в алгебраической форме:
A jB C jD A C j B D |
(5.8) |
A jB C jD AC jAD jBC j2BD
(5.9)
AC BD j AD BC
A jB |
|
A jB C jD |
|
A jB C jD |
|
C jD |
|
C jD |
C jD |
|
C2 D2 |
Пример произведения двух комплексных чисел Ee jF и зательной форме:
(5.10)
Ge jH в пока-
(Ee jF ) (Ge jH ) EG e j F H |
(5.11) |
[Показать сложение векторов на комплексной плоскости]
5.2.2 Соответствие синусоидальной и комплексной форм записи сигналов
Любому синусоидальному сигналу («оригиналу») переменной можно поставить в соответствие функцию переменной («изображение»):
f Fm sin t F m Fme j te j ,
f действительной Fm компле́ксной
(5.12)
где Fme j называется комплексной амплитудой; множитель e j t – это оператор поворота, его можно не учитывать, т. к. схема рассчитывается только на одной частоте и без учёта времени.
Изображение сигнала, как комплексное число, можно представить в алгебраической и показательной формах:
F |
m |
F e j A jB |
(5.13) |
|
m |
|
80
