method_eltech_v3.2.53_2013-11-17

I/1 I/2 I//1 I//2

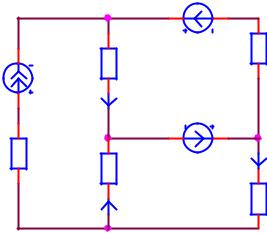
Рис. 3.4. Иллюстрация к принципу взаимности: частному случаю с источником э. д. с. (а, б), частному случаю с источником тока (в, г)

Мощность элемента электрической схемы представляет собой его способность потреблять или создавать электрическую энергию:

Активная мощность двухполюсника равна произведению напряжения на элементе и тока элемента:

Отрицательный знак в выражении для мощности источника э. д. с. объясняется тем, что ток через такой элемент обычно берётся в направлении, противоположном условно-положительному направлению тока (входящему через положительный узел).

Уравнение баланса мощностей записывается в следующем виде:

31

В некоторых случаях элемент, формально являющийся «источником энергии», сам может быть потребителем (т. е. его потребляемая мощность положительной). Это может происходить тогда, когда в цепи действуют другие, более мощные, источники питания. Показателем такого случая является обратное направление напряжения или тока, что автоматически приводит к обратному по знаку значению мощности.

32

4 Методы расчёта резистивных схем

4.1. Особенности моделирования и расчёта схем в статическом режиме. — 4.2. Расчёт по законам Кирхгофа. — 4.3. Метод непосредственного (эквивалентного) преобразования элементов. — 4.4. Принцип и метод наложения. — 4.5. Метод эквивалентного источника.

— 4.5.1. Условие отбора приёмником максимальной мощности от источника. — 4.6. Метод узловых потенциалов. — 4.7. Метод контурных токов.

Equation Section (Next)

4.1Особенности моделирования и расчёта схем

встатическом режиме

Вданной главе рассматриваются методы расчёта, применяемые при анализе линейных схем в статическом режиме, т. е. при постоянных сигналах.

Всоответствии с компонентными уравнениями (1.8) и (1.11), при постоянном токе напряжение на индуктивности равно нулю, а при постоянном напряжении ток ёмкости равен нулю:

Соответственно, в статическом режиме индуктивные элементы заменяются проводниками, а ёмкостные элементы заменяются разрывами – т. е. своими внутренними сопротивлениями.

Рис. 4.1. Замена идеальной индуктивности и ёмкости

встатическом режиме

Всхеме остаются только постоянные источники питания и сопротивления; такие схемы называются резистивными. Методы расчёта, рассмотренные для резистивных схем, лишь с небольшими изменениями применяются и для расчёта более сложных схем в динамических режимах.

Вданной главе рассмотрены следующие основные методы и принципы расчёта резистивных схем: а) расчёт цепей по законам Кирхгофа, б) метод эквивалентного преобразования элементов, в) метод наложения, г) метод эквивалентного источника, д) метод узловых потенциалов, е) метод контурных токов.

33

Задача расчёта схемы по любому из методов обычно ставится следующим образом: заданы топология схемы и параметры элементов схемы ( R , E , J ), требуется найти все или некоторые токи и напряжения схемы.

4.2 Расчёт по законам Кирхгофа

Метод решения электрических схем на основе ЗТК и ЗНК предназначен, прежде всего, для нахождения токов во всех ветвях. Обладая этой информацией, можно при помощи закона Ома и компонентных уравнений найти и напряжения во всех узлах, а также другие электрические параметры схемы.

Для решения схемы составляется совместная система уравнений по ЗТК и ЗНК. Размерность этой системы совпадает с количеством неизвестных. В общем случае уравнения дифференциальные, в случае линейной схемы уравнения линейные дифференциальные, а в случае линейной резистивной схемы уравнения линейные алгебраические.

Уравнения по ЗТК. Количество независимых уравнений по ЗТК равно количеству ветвей дерева, т. е. количеству главных сечений:

где NУ – количество узлов схемы.

* Заметим, что сумма любых j уравнений есть уравнение для такой замкнутой поверхности, которая охватывает данные j узлов. Это следует из того, что токи тех ветвей, которые не пронизывают поверхность, но находятся внутри замкнутой поверхности, войдут в уравнения два раза: один со знаком «—», другой со знаком «+». Если поверхность охватывает NУ–1 узлов, то сумма токов ветвей, пронизывающих эту поверхность, равна с обратным знаком сумме токов для У-го узла, и поэтому У-е уравнение оказывается следствием предыдущих NУ–1 уравнений.

Систему уравнений по ЗТК можно составить для узлов или формализованно для главных сечений.

Уравнения по ЗНК. Количество независимых уравнений по ЗНК равно количеству ветвей связи, т. е. количеству главных контуров:

где NВ – количество ветвей схемы.

В случае, если ищутся только токи ветвей, то в этом случае количество уравнений и неизвестных уменьшается на количество особых ветвей с известными токами (NJ):

В этом случае для системы следует выбирать контуры, не содержащие ветвей с известными токами (например, с источниками тока).

34

* Независимость контурных уравнений («независимость контуров») обеспечивается, если эти контуры выбирать так, чтобы каждый последующий отличался от предыдущих, по крайней мере, одной новой ветвью.

Систему уравнений по ЗНК можно составить для ячеек или формализованно для главных контуров. Более подробные сведения о топологических матрицах см. в Главе 2.

4.2.1 Составление уравнений по ЗТК для узлов

Уравнения составляются по первому закону Кирхгофа для узлов. При выборе узлов, для которых записывается ЗТК, имеет смысл исключить узел, к которому сходится наибольшее количество ветвей (чтобы уменьшить сложность уравнений). Токи, вытекающие из узла, суммируются со знаком «+», втекающие – со знаком «–». Для схемы рис. 4.2 можно составить следующую систему:

Рис. 4.2. Пример для составления системы уравнений по законам Кирхгофа

4.2.2 Формализованный способ составления уравнений по ЗТК

Уравнения составляются по первому закону Кирхгофа для главных сечений (см. рис. 2-7, в, г, д). Направление главного сечения определяется направлением ветви дерева, задающей данное главное сечение. Токи ветвей, входящих в данное главное сечение и сонаправленных с ним, входят в

35

сумму со знаком «+», противонаправленных – со знаком «–». Для схемы рис. 2-4 можно составить следующую систему:

4.2.3 Составление уравнений по ЗНК для ячеек

Уравнения составляются по второму закону Кирхгофа для произвольных контуров (рекомендуется выбирать ячейки, т. е. контура, не имеющие внутренних ветвей). Направление обхода выбирается произвольно. Со знаком «+» суммируются напряжения ветвей, ориентированных сонаправленно обходу контура, со знаком «–» суммируются напряжения противонаправленных ветвей. Для схемы рис. 4.2 можно составить следующую систему уравнений:

КIII : I6R6 I5R5 E4

Вслучае, если ищутся только токи ветвей, не нужно составлять уравнение для первого контура, содержащего источник тока, и система (4.9) записывается в виде:

где R — диагональная матрица сопротивлений.

4.2.4 Формализованный способ составления уравнений по ЗНК

Уравнения составляются по второму закону Кирхгофа для главных контуров. Направление обхода главного контура определяется направлением ветви связи. Со знаком «+» суммируются напряжения ветвей, ориентированных сонаправленно обходу контура, со знаком «–» суммируются напряжения противонаправленных ветвей. Для схемы рис. 2-4 (главные контура на рис. 2-8):

36

ствует порядку перечисления уравнений; порядок колонок матрицы соответствует порядку перечисления неизвестных в столбце неизвестных.

Матрицу можно составить непосредственно, т. е. без предварительной записи самих уравнений, а затем решить специальными матричными методами:

привести матрицу к единичному виду;

с помощью определителей;

с помощью математических программ, реализующих общие методы (MathCAD, Mathlab, Maple и т. п.).

Врезультате решения системы уравнений (4.16) или (4.15) или матрицы (4.17) или (4.18) получается вектор токов.

Система, составленная формализованным методом, задаёт нужное количество независимых уравнений: уравнения по ЗТК составляются для главных сечений, т. е. для ветвей дерева (т. к. каждое главное сечение включает одну и только одну ветвь дерева); уравнения по ЗНК составляются для главных контуров, т. е. для ветвей связи (т. к. каждый главный контур включает одну и только одну ветвь связи). Таким образом, каждое из уравнений включает одну новую переменную и одну новую связь. Т. к.

каждая ветвь графа является либо ветвью дерева, либо ветвью связи, то общее количество уравнений равно количеству ветвей, т. е. количеству неизвестных токов (что и требовалось).

4.2.6* Связи между топологическими матрицами

Матрицы соединений (узлов), главных контуров и главных сечений можно представить состоящими из двух подматриц: [A] [A1 : A2 ], [Qг] [Q1 :1], [Kг] [1: K2 ]. Аналогично вектора токов и напряжений ветвей могут быть представлены двумя столбцовыми блоками (номера строк

1…У–1,У…В):

При таком разбиении матриц матричные уравнения для законов Кирхгофа могут быть записаны в виде произведения блочных матриц:

Каждое сечение разрезает одну ветвь дерева и некоторые ветви связи. Из этого вытекает, что ветвь, определяющая сечение, непременно входит в контуры, образованные теми связями графа, которые разрезаются сечением, т. к. разрезание данной ветви дерева графа прведёт к разрезанию всех контуров, которые образованы связями сечения.

[после примера Демирчяна] Для всех контуров и сечений можно заметить следующую закономерность. Столбцы подматрицы [K1] могут быть образованы строками подматрицы [Q2], если у всех ненулевых элементов изменить знаки:

Следовательно, для составления матриц [K] и [Q] достаточно составить одну подматрицу [F], выражаемую через матрицу соединений [A]

следующим образом. При умножении уравнения A1Iд A2Iс (см. (4.21)) слева на [A1 1] получаем A1 1A1Iд A1 1A2Iс , что даёт Iд A1 1A2Iс . Из сравнения с уравнением Iд Q2Iс (см. (4.22)) получаем Q2 A1 1A2 , от-

куда окончательно

Последнее соотношение важно в том смысле, что оно позволяет по матрице соединений путём матричных операций составлять матрицы контуров и сечений, что исключительно важно при использовании ЭВМ, расчёты на которых требуют формализации процедуры составления систем уравнений. Для графа схемы всегда существует подматрица D2, поэтому из равенства Q2 A1 1A2 и существования A2 вытекает и существование обратной матрицы A1 1 . Можно показать, что определитель матрицы A1 существует всегда и равен ±1.

4.3 Метод непосредственного (эквивалентного) преобразования элементов

(При рассмотрении этой темы до лекции «Законы электротехники» следует предварительно напомнить особенности статического режима (замену емкостей и индуктивностей), законы Ома и Кирхгофа, задачу анализа схемы; дать определения последовательного и параллельного соединения элементов)

При решении схемы методом непосредственного преобразования элементов используют серию эквивалентных преобразований схемы, направленных на упрощение схемы. Понятие эквивалентного преобразования подразумевает такое изменение состава и/или топологии (способа соединения элементов) фрагмента схемы, при котором не изменяются электрические показатели (токи и напряжения) в остальных частях схемы,

40