
method_eltech_v3.2.53_2013-11-17
.pdf
Для решения дифференциального уравнения требуется составить характеристическое уравнение. Оно получается при помощи замены операции дифференцирования умножением на переменную p . Для линейного дифференциального уравнения с постоянными коэффициентами характеристическое уравнение представляет собой обычный многочлен:
a pn a |
p a |
0 |
(6.10) |
|
n |
1 |
0 |
|
|
В зависимости от порядка n (количества корней) характеристического уравнения и соотношения между корнями, различной будет и форма решения. В случае 1-го или 2-го порядка решение представляется в аналитическом виде (в виде формулы), в случае 3-го или большего порядка решение обычно находится численными методами.
6.4.1 Этап 3а. Определение принуждённой составляющей решения
Принуждённая составляющая решения представляет собой предел, к которому стремится переходной процесс. Для её нахождения составляется вспомогательная схема СПС2 («схема второго принуждённого состояния»); она образуется из исходной схемы с учётом коммутации. Принуждённое состояние по схеме СПС2 рассчитывается в режиме постоянного или переменного тока (в зависимости от состава схемы и входных сигналов) соответствующими методами. По схеме определяются искомые величины, а если предполагаются последующие коммутации, то также напряжения конденсаторов и токи индуктивностей.
6.4.2 Этап 3б. Определение свободной составляющей решения
В случае, если порядок схемы 1-й или 2-й, то форма свободной составляющей решения известна и зависит от соотношения корней.
Порядок уравнения и характер переходного процесса определяются по вспомогательной схеме ССС («схеме для определения свободных составляющих»). Для составления этой схемы необходимо в исходной схеме выполнить коммутацию в соответствии с условиями задачи, обнулить независимые источники питания, затем пределельно упростить схему с помощью методов преобразования элементов. Количество реактивных элементов в преобразованной схеме определяет порядок n схемы.
1) n 1. Свободная составляющая решения находится по формуле:
i (t) Ae t . |
(6.11) |
св |
|
Постоянная времени вычисляется, соответственно, как |
|
RэCэ или Lэ Rэ |
(6.12) |
2) n 2. Корни характеристического уравнения можно найти методом входного сопротивления. В соответствии с этим методом, все элемен-
101

ты схемы после коммутации заменяют их комплексными сопротивлениями (с использованием замены переменных p j ), и обнуляют независимые источники; затем ветвь, в которой ищется ток, разрывается, и по отношению к точкам разрыва ищется комплексное входное сопротивление схемы Zвх( p) . Уравнение Zвх( p) 0 имеет те же корни (два корня при n 2), что и характеристическое уравнение схемы. В зависимости от соотношения корней выделяются три случая:
а. D 0 , два различных действительных корня p1 p2 0 :
i (t) Ae p1t Be p2t , |
1 |
|
|
(6.13) |
min |
|
p |
||
св |
|
|
б. D 0 , два совпадающих действительных корня p1 p2 0 :
i |
(t) (A Bt)e p1t , |
1 |
(6.14) |
|
p1 |
||||
св |
|
|
в. D 0 , два комплексно-сопряжённых корня p1,2 j :
i |
(t) Ae t sin( t B) , |
1 |
, T |
2 |
(6.15) |
|
|
|
|||||
св |
|
|
|
Определение постоянных интегрирования. Для определения постоянных интегрирования (коэффициентов A и B в уравнениях (6.12) — (6.15)) необходимо составить одно или два дополнительных уравнения для сигналов при t 0 (для начальных условий).
1) n 1. Общий вид решения:
i(t) iпр(t) iсв(t) iпр(t) Ae t
Начальные условия (при t 0 ):
|
i( 0) iпр( 0) A |
|
|
A i( 0) iпр( 0) |
||||||||
Окончательное решение: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
i(t) iпр(t) iпр( 0) |
i( 0) e |
|
|||||||||
|
|
СПС |
|
|
|
СНУ |
ССС |
|||||
2) n 2: |
|
|
|
|
|
|
|
|
|
|
|
|
а. p1 p2 |
: |
|
|
и его производной i/ (t) : |
||||||||
Общий вид решения i(t) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
(t) Ae |
p1t |
Be |
p2t |
|
||||
|
i(t) iпр |
|
|
|
|
|||||||
|
/ |
(t) i |
/ |
|
(t) Ap e |
p t |
|
p t |
||||
|
i |
|
|
1 Bp e 2 |
||||||||
|
t |
t пр |
|
|
|
1 |
|
|
2 |
|||
Начальные условия (при t 0):
(6.16)
(6.17)
(6.18)
(6.19)
102

i( 0) i |
( 0) A B |
|
|
||
|
пр |
|
|
|
(6.20) |
i/ ( 0) i/ |
|
( 0) Ap |
Bp |
||
|
t пр |
1 |
2 |
|
|
t |
|
||||
Система (6.20) представляет собой систему двух линейных уравнений с двумя неизвестными: A и B , которые находятся однозначно.
б. p1 |
p2 |
: |
|
|
|
|
Общий вид решения i(t) и его производной i/ (t) : |
||||||
|
|
|
|
|
|
t |
|
|
i(t) i |
(t) A Bt e p1t |
|
||
|
|
|
пр |
|
|
|
|
|
|
|
|
(t) Be p1t p |
A Bt e p1t |
|
|
i/ (t) i/ |
|
|||
|
|
t |
t пр |
1 |
|
|
Начальные условия (при t 0):
i( 0) i |
( 0) A |
||
|
пр |
|
|
i/ ( 0) i/ |
|
( 0) B Ap |
|
|
t пр |
1 |
|
t |
|||
(6.21)
(6.22)
Система (6.22) также представляет собой систему двух линейных уравнений с двумя неизвестными: A и B , которые находятся однозначно.
в. p1,2 j : /
Общий вид решения i(t) и его производной it (t) :
i(t) i |
|
(t) Ae t |
sin t B |
|||
|
пр |
|
|
|
|
|
|
|
|
|
(t) Ae t sin t B Ae t cos t B |
||
i/ (t) i/ |
|
|||||
t |
|
t пр |
|
|
|
|
Начальные условия (при t 0): |
||||||
|
|
i( 0) i |
( 0) Asin B |
|||
|
|
|
пр |
|
|
|
|
|
i/ ( 0) i/ |
|
( 0) Asin B Acos B |
||
|
|
|
t пр |
|
||
|
|
t |
|
|||
(6.23)
(6.24)
Из системы (6.24) находятся выражения Asin B и Acos B , откуда вычисляются A и tg B , из последнего отыскивается B .
6.5 Этап 3. t 0 .
Операторный метод расчёта переходного процесса
6.5.1 Основные свойства операторного преобразования
Основная трудность классического метода расчёта переходных процессов заключается в определении постоянных интегрирования по начальным условиям. В операторном методе, предложенном Хэвисайдом, действительные функции времени («оригиналы») заменяются соответствующими операторными «изображениями». При этом дифференциальные
103
уравнения для оригиналов заменяются алгебраическими уравнениями для изображений.
Соответствие между оригиналом f (t) и изображением F( p) устанавливается с помощью преобразования (интеграла) Лапласа:
|
|
f (t) F( p) f (t)e pt dt , |
(6.25) |
0 |
|
где p a jb – комплексное число. Все реальные сигналы удовлетворяют условиям на сходимость подынтегральной функции.
В (6.26) приведены некоторые распространённые соответствия, а в (6.27) некоторые распространённые операции над оригиналами и изображениями.
1 t |
1 |
|
|
|
sin t |
|
cos psin |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
p2 2 |
|
|
|||||||||
p |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
t 1 |
|
e t sin t |
|
|
|
|
|
|
|
||||||||||||
|
p |
2 |
|
2 |
|
||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
e |
t |
|
|
|
|
|
te |
t |
|
|
|
1 |
|
|
|
|
|
||||
|
|
p |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
p 2 |
|
|
|
|
|||||||||
|
t |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
p2 |
|
1 e t |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
p p |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fk (t) |
|
Fk ( p) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
k 1 |
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
a f (t) a F( p) |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
ft/ (t) pF( p) f ( 0) |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
F( p) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
f (t)dt |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(6.26)
(6.27)
6.5.2Компонентные уравнения в операторной форме
Втабл. 6.2 показан вид компонентных уравнений в операторной форме для двухполюсных элементов.
104
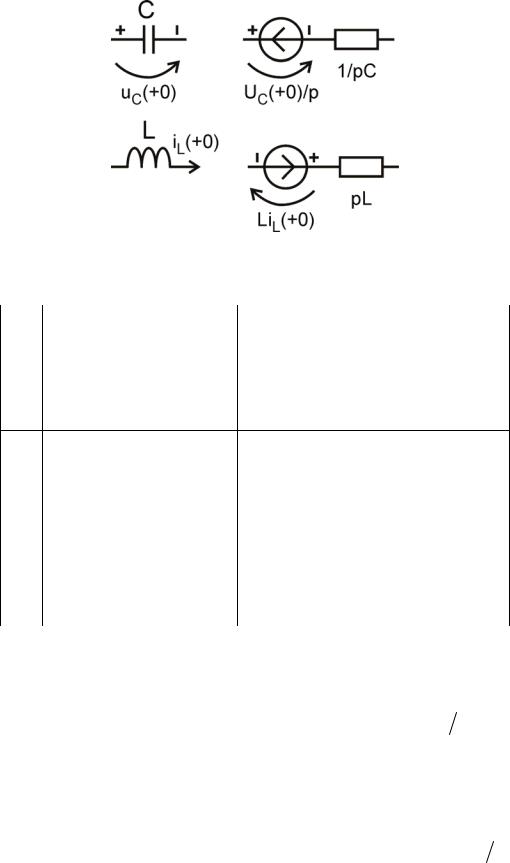
Рис. 6.3. Преобразование реактивных элементов для ОСЗ
Табл. 6.2. Компонентные уравнения в операторной форме
|
Исходная |
Операторная |
|
схема замещения |
схема замещения |
E: |
e(t) |
E( p) |
|
|
|
J: |
j(t) |
J ( p) |
|
R: |
|
uR R iR |
|
|
|
|
|
UR ( p) R IR ( p) |
|
|
|
|||||
|
|
|
1 T |
|
|
|
|
|
u ( 0) |
|
1 |
|
|
|
|
||
|
C: |
u |
|
i dt u |
( 0) |
U |
C |
( p) C |
|
|
I |
C |
( p) |
||||
|
pC |
||||||||||||||||
|
|
C |
C C |
C |
|
|
p |
|
|
|
|
||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
L: |
|
uL L |
diL |
|
|
|
UL ( p) pL IL ( p) Li( 0) |
|||||||||
|
|
dt |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зако- |
|||||||||||||||
Если последние три выражения из табл. 6.2 представить в виде |
|||||||||||||||||
на Ома, то коэффициенты связи между операторным напряжением и операторным током можно назвать операторными сопротивлениями соответствующих элементов: операторное сопротивление резистора получается равным R , операторное сопротивление ёмкости получается 1 pC , а операторное сопротивление индуктивности получается pL .
В результате перевода компонентных уравнений в операторную форму, все они принимают вид закона Ома. Таким образом, для анализа и расчёта схемы можно заменить каждый пассивный элемент его опера-
торным сопротивлением; последовательно с операторным сопротивлени- |
||||||
ем |
подключается постоянный |
источник э. д. с. или |
u |
0 p |
или |
|
Li |
0 , соответственно, |
|
C |
|
|
|
выражающий запас электро-магнитной |
||||||
|
L |
|
|
|
|
|
энергии, накопленной в элементе к началу коммутации. Получаемая при
105
этом резистивная схема замещения называется операторной схемой замещения (ОСЗ). Для её анализа и расчёта применяется вся уже известная методика анализа и расчёта схем по постоянному сигналу с единственным отличием: все сигналы записываются в операторной форме.
6.5.3 Получение изображения переходного процесса и переход от изображения к оригиналу
В результате перевода интегрально-дифференциальных топологических уравнений в операторную форму они принимают вид линейных алгебраических уравнений. По схеме ОСЗ рассчитываются изображения искомых функций любыми известными методами. От этих изображений затем можно перейти к функциям времени с помощью таблиц соответствия или по теореме разложения.
Изображения электрических сигналов, как правило, представляются в виде рациональных дробей:
|
F ( p) |
|
a pm a |
|
pm 1 a |
|
|
|
F( p) |
1 |
|
m |
m 1 |
0 |
, |
(6.28) |
|
F2 ( p) |
|
|
|
|||||
|
|
b pn b |
pn 1 b |
|
|
|||
|
|
|
n |
n 1 |
|
0 |
|
|
где для всех реальных сигналов m n .
Рациональную дробь можно разложить на простейшие дроби:
|
|
|
F1( p) |
A1 |
|
|
|
|
|
A2 |
|
|
|
|
|
|
An |
|
|
|
n |
Ak |
|
|
||||||
F( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
F ( p) |
|
p p |
|
p p |
|
|
p p |
|
p |
p |
|
, (6.29) |
||||||||||||||||||
2 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
n |
|
k 1 |
|
|
k |
||||||
где pk ,k |
|
– корни уравнения F2 |
p 0 |
|
– полюса функции F p . |
|||||||||||||||||||||||||
1,n |
||||||||||||||||||||||||||||||
Такой способ представления называется «сумма вычетов в особых |
||||||||||||||||||||||||||||||
точках». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Коэффициенты Ak |
выражаются как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
A |
F1 pk |
|
|
|
|
|
|
|
|
|
|
(6.30) |
|||||||||
|
|
|
|
|
|
|
|
|
F / p |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
F1 pk |
|
n |
|
|
A |
|
|
|
n |
F1 pk |
1 |
|
|
|
|
|
||||||||||
|
|
F( p) |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
(6.31) |
|||||
|
|
F2 pk |
|
|
|
|
|
|
/ |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
k 1 |
p pk |
k 1 |
F2 pk p pk |
|
|
|
|
||||||||||||||||||
А так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
e pk t , то |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
p pk |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
106

|
F |
p |
|
|
|
|
|
n |
F |
p |
|
|
p t |
|||
F( p) |
1 |
|
|
|
|
f (t) |
1 |
|
k |
|
e |
|||||
|
|
|
|
|
|
|
|
|
k |
|||||||
F2 |
p |
|
/ |
|
pk |
|||||||||||
|
|
|
|
|
|
k 1 |
F2 |
|
|
|
||||||
Величины |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
p |
|
|
|
F1 pk |
|
e pk t |
|
|
|||||
Res |
e pt |
|
|
|
|
|||||||||||
F2 |
|
F2/ pk |
|
|
||||||||||||
p pk |
p |
|
|
|
|
|
|
|||||||||
(6.32)
(6.33)
как раз и являются вычетами функции F p , берущимися во всех полюсах pk функции F p .
Формула (6.32) применима в общем случае.
Если один из корней уравнения F2 p 0 равен нулю (пусть это p1 ), то вычет, относящийся к этому корню, равен:
F1(0) |
|
1 |
|
|
F1(0) |
(6.34) |
|
|
F2/ (0) |
||||
F2/ (0) p |
|
|||||
Если среди корней уравнения F2 p 0 есть пара комплексносопряжённых, то мнимые части вычетов, относящихся к этим корням, оказываются противоположными по знаку и сокращаются; действительные части их вычетов равны:
F |
p |
|
e pk t |
F1 |
pk* |
* |
|
F |
p |
k |
|
|
|
||
1 |
k |
|
|
|
|
|
e pk t 2Re |
|
1 |
|
|
e pk t |
(6.35) |
||
F / p |
|
F / |
|
p* |
|
|
|
|
|
||||||
|
|
F / p |
|
|
|||||||||||
2 |
k |
|
|
2 |
k |
|
|
2 |
|
k |
|
|
|
||
Если среди корней уравнения F2 p 0 есть пара кратных корней (пусть p1 p2 ), то вычеты, относящиеся к этим корням, равны:
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
F1 p |
|
|
|
|
|
lim |
|
|
|
|
|
e |
pt |
(6.36) |
||
dp |
|
|
F2 p |
|
|
|
||||
p pk |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
p p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.6 Примеры расчёта переходных процессов классическим методом
□ Пример 15. В момент времени t 0 в схеме рис. 6.4, а замыкается ключ. Требуется найти выражение для тока i(t) , построить график до и после коммутации в диапазоне времени ;5 .
1. t 0 . Определяем принуждённые составляющие до коммутации по схеме рис. 6.4, б (по постоянному сигналу, т. к. в схеме нет переменных источников):
107

iпр(t) J4 , uC (t) uab,пр(t) E1 R1J4 c
Так как эти функции фактически не зависят от времени, то их значения при t 0 будут равны указанным.
2. t 0 . а) Определяем независимые начальные условия по законам коммутации:
uC ( 0) uC ( 0) c
б) Определяем зависимые начальные условия по схеме СНУ (рис. 6.4, в), методом наложения:
i( 0) |
|
|
E1 |
|
|
|
uC ( 0) |
|
|
|
R3 |
a . |
||
R |
R |
|| R |
R |
|
|
R |
R |
|||||||
|
|
|
|
R |
|| R |
|
|
|||||||
|
|
1 |
2 |
3 |
|
2 |
1 |
|
3 |
|
1 |
3 |
|
|
3. t 0 . а) Определяем принуждённую составляющую тока по схеме СПС (рис. 6.4, г):
i |
(t) |
|
E |
b |
|
|
|||
пр |
|
R1 |
R3 |
|
|
|
|||
б) Определяем свободную составляющую тока по схеме ССС (рис. 6.4, д). После упрощения схемы ССС (рис. 6.4, е) получаем схему, состоящую из одного контура с ёмкостью. Таким образом, это схема первого порядка, форма решения для неё определяется формулой (6.18), а постоянная времени формулой (6.12).
в) Определяем окончательное решение по формуле (6.18): i(t) iпр(t) iсв(t) iпр(t) Ae t
iпр(t) iпр( 0) i( 0) e t b b a e t
b b a e t
г) График тока i(t) до и после коммутации в диапазоне времени
;5 :
. ■
108
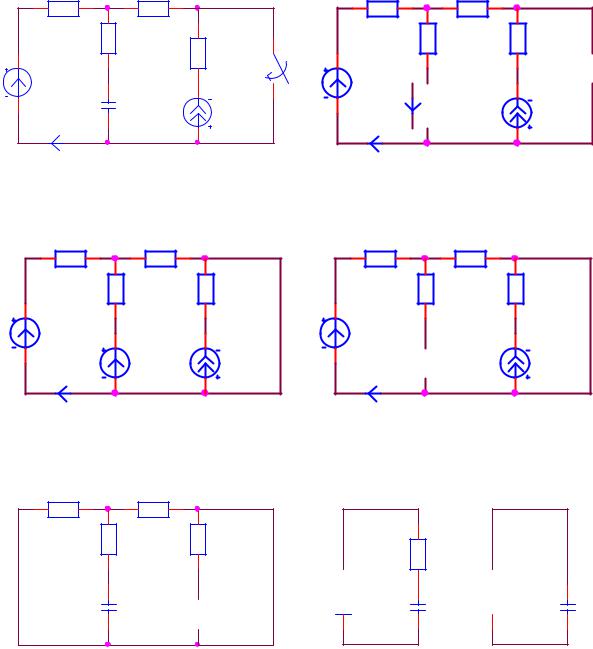
R1 |
R3 |
|
R1 |
R3 |
|
|
|
R2 |
R4 |
|
R2 |
R4 |
|
E1 |
t=0 |
E1 |
||||
|
|
|
||||
|
|
|
|
|||
|
|
К1 |
|
|
J4 |
|
|
C2 |
J4 |
|
u C (t) |
||
i(t) |
i(t) |
|
||||
|
|
|
|
|||
|
(а) исходная |
|
|
(б) 1. СПС |
|
|
R1 |
R3 |
|
R1 |
R3 |
|
|
E1 |
R2 |
R4 |
E1 |
R2 |
R4 |
|
|
|
|
|
|||
|
uC (+0) |
J4 |
|
|
J4 |
|
i(+0) |
|
|
iпр(t) |
|
||
|
|
|
|
|||
|
(в) 2. СНУ |
|
|
(г) 3а. СПС |
|
R1 R3
R2 R4
C2


 R1 || R3
R1 || R3
R2
C2


 (R1 || R3) + R2
(R1 || R3) + R2
C2
(д) 3б. ССС (е) 3б. ССС–преобр.
Рис. 6.4. Вспомогательные схемы к отысканию переходного процесса классическим методом: а) исходная схема, б) схема СПС1 — состояние до коммутации, в) схема СНУ— зависимые начальные условия,
г) схема СПС —принуждённая составляющая, д),е) схема ССС — свободная составляющая
109
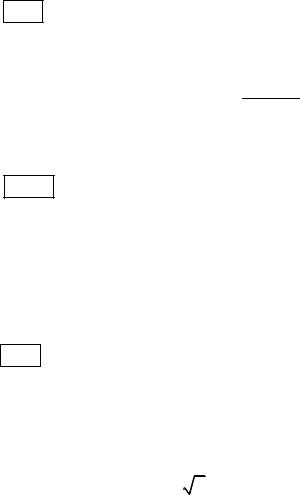
□ Пример 16. В момент времени t 0 в схеме рис. 6.5, а ключ переключается из положения 1 в положение 2. Требуется найти выражение для тока i3(t) , построить график до и после коммутации в диапазоне времени ;5 . Источник e1(t) E1.
□ Пример 17. В момент времени t 0 в схеме рис. 6.5, а ключ переключается из положения 1 в положение 2. Требуется найти выражение для тока i3(t) , построить график до и после коммутации в диапазоне
времени ;5 . Источник e1(t) E1,m sin( t ) .
1. t 0 . Определяем принуждённые составляющие до коммутации по схеме рис. 6.5, б (по постоянному сигналу, т. к. в схеме нет переменных источников):
i3пр(t) iL3пр(t) R2E3R3 a
Так как эти функции фактически не зависят от времени, то их значения при t 0 будут равны указанным.
2. t 0 . а) Определяем независимые начальные условия по законам коммутации:
iL3( 0) iL3( 0) b
б) Определяем зависимые начальные условия по схеме СНУ (рис. 6.5, в):
i3( 0) iL3( 0) b
3. t 0 . а) Определяем принуждённую составляющую тока по схеме СПС (рис. 6.5, г) (комплексным методом, т. к. в схеме есть переменные источники):
I 3,пр |
E1 |
|
Ae |
j |
R R jX |
|
|
||
|
1 3 |
L3 |
|
|
i3пр(t) A 2 sin t
110
