Переходная функция инерционного звена представляет собой экспоненту с постоянной времени Т (рис. 6.36, а).
Передаточная функция звена будет
W( p) |
xвых( p) |
|
K |
. |
(6.45) |
|
|
|
xвх( p) |
Tp 1 |
|
Амплитудно-фазовая характеристика звена |
|
|
|
W( j ) A( ) ej ( ) |
|
K |
j arctg(T ). (6.46) |
|
|
|
e |
|
|
|
|
1 (T )2 |
|
Итак, рассмотрев различные системы, относящиеся к двум типовым динамическим звеньям, мы показали, что они могут описываться общими уравнениями, устанавливающими связь между выходными и входными величинами. Ограниченность объема учебного пособия не позволяет рассмотреть остальные типовые динамические звенья.
6.4.9.6. Основные виды соединений звеньев системы
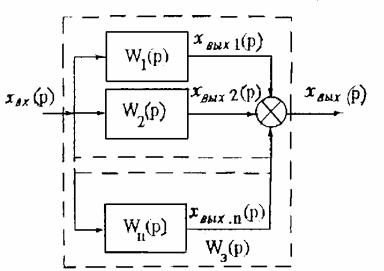
Различные сложные соединения звеньев основываются в основном на трех типовых соединениях: последовательном, параллельном и встречнопараллельном (соединение с обратной связью). Рассмотрим их основные уравнения.
Рис. 6.37. Схема последовательного соединения звеньев
Последовательное соединение (рис. 6.37). Передаточная функция n
последовательно соединенных звеньев, равна произведению передаточных функций этих звеньев:
|
|
|
xвыхn( p ) |
|
n |
|
WЭ |
( p ) |
|
W1( p ) W2( p )...Wn( p ) Wi( p ). (6.47) |
|
xвх( p ) |
|
|
|
i 1 |
Параллельное соединение (рис. 6.38). Передаточная функция параллельного соединения звеньев WЭ(р) равна сумме передаточных функций этих звеньев:
n |
|
WЭ (p) Wi (p). |
(6.48) |
i 1 |
|
Рис. 6.38. Схема параллельного соединения звеньев
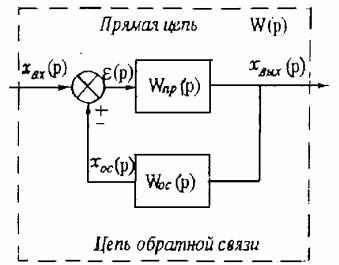
Соединение с обратной связью (рис. 6.39) характеризуется наличием цепи передачи выходного сигнала на вход системы. В системах автоматического регулирования бывает основная обратная связь, как правило, отрицательная, и дополнительные обратные связи, предназначенные для коррекции динамических характеристик отдельных звеньев. Последние могут быть как отрицательными, так и положительными.
На основе приведенных трех типовых соединений звеньев создаются более сложные структурные схемы реальных АСР.
Рис. 6.39. Схема системы с обратной связью
Как видно, выходной сигнал прямой цепи, он же выходной сигнал системы xвых(p), через цепь обратной связи в виде хос(р) подается на вход системы. Результат рассогласования ε(p) входного сигнала и сигнала обратной связи подается на вход системы. На основании несложных рассуждений с учетом вышеприведенных правил для последовательного и параллельного соединений звеньев получаем выражение для передаточной функции замкнутой системы:
W(p) |
x |
(p) |
Wnp |
(p) |
|
вых |
|
|
|
|
, |
(6.49) |
|
|
|
|
|
xвх(p) |
1 Wnp(p) WOC (p) |
|
где знаки (+) и (-) соответствуют отрицательной и положительной обратным связям.
6.4.9.7. Устойчивость автоматических систем регулирования. Понятия об устойчивости
Одним из важных и необходимых условий работоспособности АСР является их устойчивость. АСР находится в состоянии равновесия, если регулируемая величина не изменяется во времени. Процесс регулирования устойчив, если после отклонения АСР от положения равновесия и устранения возмущения, вызвавшего это отклонение, она вновь с течением времени возвратится к исходному состоянию.
Различают три вида состояний равновесия: 1) устойчивое; 2) безразличное; 3) неустойчивое. Эти виды равновесия схематически представлены на рис. 6.40 с помощью различного расположения шариков.
610

Рис. 6.40. Схема, иллюстрирующая виды равновесия: а - безразличное равновесие; б и г - устойчивое равновесие; в - неустойчивое равновесие
Математически задача устойчивости была решена Л.М. Ляпуновым. Так как это решение справедливо для малых отклонений, то при исследовании исходят из линеаризированных дифференциальных уравнений. В соответствии с вышеприведенным определением устойчивости системы ее поведение характеризуется свободным движением. Решение дифференциального уравнения системы состоит из свободной и вынужденной составляющих. Вынужденная составляющая движения определяется возмущающими воздействиями и свойствами самой системы. Свободная же составляющая движения определяется только свойствами самой системы и по характеру свободного движения можно судить об основных динамических показателях системы.
Потому при исследовании устойчивости систем анализируют свободную составляющую решения, которая аналитически получается из однородного дифференциального уравнения (с нулевой правой частью):
a |
dnx |
a |
dn 1x |
a |
|
вых |
вых |
n 1 |
dtn |
|
0 |
1 dtn 1 |
|
dxвых anxвых 0. (6.50) dt
Решение уравнения (6.50) записывается так:
n |
|
xвых(t ) Ck epK t , |
(6.51) |
k 1
где Ск - постоянная интегрировании; рк - корни характеристического уравнения исходного дифференциального уравнения.
Характеристическое уравнение имеет вид
a0 pn a1 pn 1 ... an 1 p an 0 |
(6.52) |
611
B(p)
и совпадает со знаменателем передаточной функции W(p) A(p) , поэтому
может быть определено из W(p), приравниванием к нулю ее знаменателя
А(р)=0.
Система автоматического регулирования будет устойчива, если с течением времени все составляющие решения (6.51) стремятся к нулю. Корни характеристического уравнения (6.52) могут быть вещественными (в т.ч. и нулевые), комплексными и мнимыми:
pK aK ; pK βK jωK ; pK jωK .
Графики решений (6.51) имеют вид, представленный на рис. 6.41. Как видно из графиков решений, переходные процессы при
вещественных отрицательных корнях монотонно затухают, при отрицательной вещественной части комплексных корней имеют вид затухающих колебаний, а при мнимых корнях - незатухающие колебания (на рис. 6.41 не показано). Таким образом, для устойчивой линейной системы автоматического регулирования необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения были отрицательными. Однако сложность вычисления корней характеристического уравнения АСР вызвала необходимость косвенных методов оценки устойчивости систем, названных критериями устойчивости.
Критерии устойчивости. Существует ряд алгебраических критериев устойчивости (Гурвица, Раусса, И.А. Вышнеградтского), основанных на определенных соотношениях коэффициентов характеристического уравнения. Уровень сложности этих критериев зависит от порядка характеристического уравнения. На практике часто отдают предпочтение частотным критериям устойчивости (в частности, критерию Найквиста).
Частотный критерий устойчивости Найквиста. Этот критерий получил особо широкое распространение в практике расчетов систем автоматизации благодаря ряду достоинств:
612
Рис. 6.41. Переходные процессы для различных видов корней характеристического уравнения системы: а - вещественные корни; б, в -
комплексные корни
- для анализа устойчивости системы по этому критерию используется амплитудно-фазовая частотная характеристика разомкнутой системы, которая может быть получена как аналитически, так и экспериментальным путем, что особенно важно;
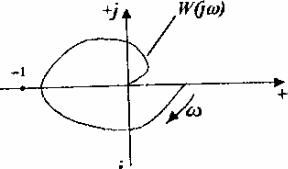
Рис. 6.42. К определению устойчивости системы по критерию Найквиста
- использование АФЧХ разомкнутой системы позволяет без риска для АСР, которая может оказаться неустойчивой в замкнутом состоянии, оценить ее устойчивость в замкнутом состоянии до аппаратурного замыкания.
Основная формулировка критерия Найквиста сводится к следующему (рис. 6.42): АСР, устойчивая в разомкнутом состоянии, будет устойчива и в замкнутом состоянии, если амплитудно-фазовая частотная характеристика разомкнутой системы не охватывает точку с координатами (-1; /0).
6.4.9.8. Качество автоматических систем регулирования
Показатели качества. Условие устойчивости АСР является необходимым, но недостаточным для практическою применения системы, т.к. переходный процесс в системах может быть либо слишком медленным, либо слишком колебательным, либо отличаться недопустимыми отклонениями регулируемой величины. Поэтому система должна отвечать определенным показателям качества регулирования. Оценка качества АСР осуществляется по характеру переходного процесса в системе, получаемого при воздействии на нее наиболее типичных возмущений. Чаще всего в качестве типового возмущающего воздействия используют ступенчатое входное воздействие, характеризующее наиболее тяжелый режим работы оборудования. Это может быть режим пуска, останова, сброса нагрузки и т.д. xвх(t)=0 при t<0; хвх(t)=а при t>0, где а - константа.
На рис 6.43 приведены перекидные процессы при обработке по управляющему (рис. 6.43, а) и возмущающему (рис. 6.43, б) воздействиям. Основными показателями качества процесса регулирования являются следующие.
Перерегулирование σ характеризует максимальное динамическое отклонение регулируемой величины х1 от исходного состояния равновесия.
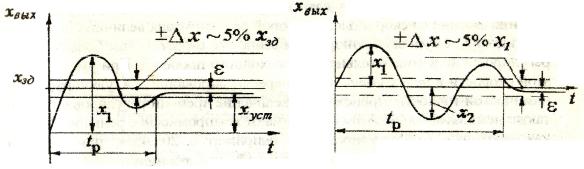
При этом для переходного процесса по управляющему воздействию (по заданию хзд, показанному на рис. 6.43, а), перерегулирование выражается в % от установившегося значения регулируемой величины:
σ x1 xуст / xуст 100. |
(6.53) |
При регулировании по возмущающему воздействию перерегулирование определяется по отношениям двух соседних амплитуд колебаний
(рис. 6.43, б):
Время регулирования tp - это промежуток времени от момента нанесения воздействия и соответствующего отклонения регулируемой величины до момента возвращения ее регулятором к исходному значению с точностью ± 5% величины максимального динамического отклонения регулируемой величины х1 (при регулировании по возмущению) или до момента достижения регулируемой величиной нового заданного значения с точностью ± 5% (при регулировании по управляющему воздействию).
Рис. 6.43. Показатели качества переходного процесса
Остаточное отклонение ε - отклонение регулируемой величины в новом установившемся режиме от заданного значения при регулировании
по управляющему воздействию, т.е. xзд xуст , а при регулировании по возмущающему воздействию ε характеризует отклонение регулируемой величины от исходного при окончании процесса регулирования (рис. 6.43, б). Итак, остаточное отклонение характеризует статическую точность системы регулирования.
Перерегулирование и время регулирования являются основными показателями качества и тесно взаимосвязаны. Действительно, перерегули-

рование связано со скоростью, с которой регулируемая величина подходит к установившемуся значению, и чем выше эта скорость, тем больше перерегулирование и колебательность переходного процесса. При уменьшении этой скорости в целях уменьшения перерегулирования, т.е. улучшения динамической точности, происходит увеличение времени регулирования, что также нежелательно. Поэтому принимают компромиссное решение, допуская некоторое перерегулирование, например в 20-45%, при котором обычно получается переходный процесс с 2-3 колебаниями. Итак, все показатели качества сводятся к двум основным показателям: статической и динамической точности регулирования.
Для уменьшения величины статической ошибки, а следовательно, повышения точности регулирования, необходимо увеличивать коэффициент усиления системы. Однако увеличение коэффициента усиления системы ведет к снижению запаса устойчивости. Это видно, например, из критерия устойчивости Найквиста, т.к. увеличение коэффициента усиления системы увеличивает модуль А(ω) амплитудно-фазовой характеристики, приближая его к критической точке [-1, j0], снижая тем самым запас устойчивости системы. Поэтому приходится идти на компромисс, допуская определенную величину статической ошибки регулирования, при которой обеспечивается необходимый запас устойчивости системы.
Методы оценки качества переходного процесса. Анализ качества АСР наиболее полно можно осуществить, построив переходный процесс. Существует ряд методов построения переходного процесса, которые отличаются друг от друга степенью трудоемкости и точности. В инженерной практике чаще пользуются приближенными методами оценки качества переходных процессов на основе либо графика вещественной частотной характеристики замкнутой системы, либо расположения корней характеристического уравнения системы на комплексной плоскости корней.
Частотный метод оценки качества. Метод позволяет установить ряд текущих зависимостей, дающих возможность оценить качество переходного процесса без его построения, но на основе анализа вещественной частотной характеристики P(ω) замкнутой системы, связанной интегральным соотношением с переходным процессом h(t):
2 P( )
h(t) sin t d . (6.55)
0
При определенных затруднениях непосредственного вычисления интеграла (6.55) прибегают к графическому вычислению указанных интегралов. Для этого вещественную частотную характеристику разбивают на типовые трапецеидальные или треугольные характеристики, для которых переходные процессы табулированы hi(t), а далее находят
n
h(t ) hi(t ).
i 1
6.5. Дискретные автоматические системы регулирования
6.5.1.Понятия о дискретных АСР и их классификация
Внепрерывных системах существуют только непрерывные сигналы, являющиеся непрерывными функциями времени. В дискретной АСР сигнал изменяется во времени дискретно, скачками. Преобразование непрерывного сигнала в дискретный называется квантованием сигнала. Существует два основных вида квантования: по уровню и по времени. В соответствии с видами квантования АСР дискретного действия делятся на три типа: релейные, импульсные и цифровые. В целом в этом разделе подробнее рассмотрим лишь релейные АСР.
6.5.2. Классификация релейных АСР
Большинство релейных АСР можно представить, как показано на рис. 6.44. Здесь НП - непрерывная часть системы, а РЭ - релейный элемент. Релейный элемент осуществляет квантование непрерывного сигнала X по уровню, преобразуя его в дискретный сигнал У. Релейный элемент - это звено релейного действия, статическая характеристика которого может иметь вид, показанный на рис. 6.45. Простейшей релейной АСР является, например, система регулирования температуры в сушильном шкафу (рис. 6.46).
НП
УX
|
|
РЭ |
|
-b |
|
b |
|
|
|
|
|
2b |
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.44. Релейная АСР |
Рис. 6.45. Статическая характеристика |
|
|
|
|
двухпозиционного регулятора |
Для измерения температуры здесь используется термометр ртутный контактный ТРК. После включения рубильника температура в сушильном шкафу СШ повышается, достигает заданной, контакты термометра ТРК
616
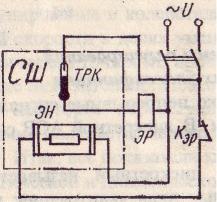
замкнуться ртутным столбиком и катушка электромагнитного реле ЭР окажется под напряжением, разомкнется контакт Кэр и электронагревательный элемент ЭН обесточится. В результате будет понижаться температура, контакты термометра ТРК разомкнутся, катушка реле ЭР обесточится, контакт Кэр замкнется и вновь начнется нагрев.
Рис. 6.46. АСР температуры в сушильном шкафу
По типу релейных элементов релейные АСР называются двухпозиционными, трехпозиционными и т.д. Многопозиционное квантование по уровню применяется главным образом в цифровых САУ. Простота релейных схем объясняется тем, что устройства релейного действия, как правило, значительно проще устройств непрерывного пропорционального действия. Релейные АСР получили широкое распространение благодаря своей простоте, однако имеют и существенные недостатки: регулируемая величина совершает незатухающие колебания около заданного значения даже при отсутствии внешних возмущающих воздействий (режим автоколебаний).
6.5.3. Автоколебания в релейных АСР
Из релейных АСР наибольшее распространение в промышленности получили системы двухпозиционного регулирования (СДР). Как следует из примера СДР температуры (см. рис. 6.46), электронагреватель сушильного шкафа может быть либо включенным, либо выключенным, а температура в его рабочем пространстве может либо возрастать, либо уменьшаться относительно заданного значения. Этот режим работы релейных систем регулирования называется автоколебательным, а возникшие незатухающие колебания регулируемой величины - автоколебаниями (автономными колебаниями).
Качество переходного процесса при регулировании в таких системах определяется параметрами автоколебаний - амплитудой и частотой (или периодом). Анализ автоколебаний в СДР ведется на основе ее структурной схемы, представляющей последовательное соединение релейного двухпозиционного регулятора - релейного элемента РЭ и линейной части с пере-