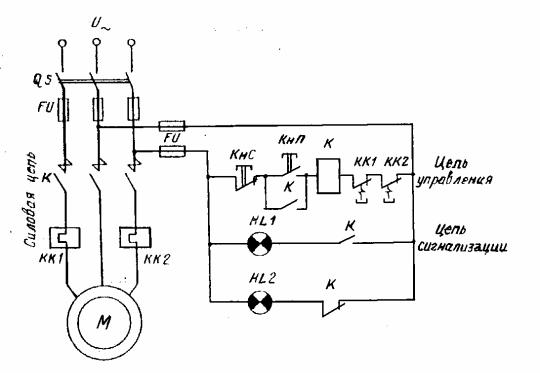
Общие принципы построения релейных схем на примере схем блокировки при кнопочном управлении сводятся к следующему. При блокировке в результате взаимосвязи отдельных элементов обеспечивается определенная последовательность включения ряда устройств (механизмов) или выполнения технологических операций. Так, для нормального функционирования схемы с кнопочным управлением применяют самоблокировку в виде параллельного включения замыкающего контакта К. Благодаря этому после включения контактора с помощью кнопки КнП «Пуск» цепь питания катушки сохраняется независимо от положения кнопки.
Рис. 6.29. Принципиальная схема управления асинхронным двигателем с магнитным пускателем
Для бесконтактного управления асинхронными приводами в силовую цепь включают тиристорные коммутаторы. Тиристорные устройства благодаря небольшим габаритным размерам и массе, практической безынерционности, хорошим надежностным характеристикам, обеспечиваемым бесконтактными схемами управления, оказываются вне конкуренции по сравнению с другими устройствами преобразования и управления.
6.4.9. Основные характеристики элементов и линейных систем автоматического регулирования непрерывного действия
Исследование элементов и систем автоматического регулирования (управления) связано с изучением процессов, в них протекающих. Характер этих процессов описывается с помощью различных зависимостей, основанных на определенных физико-механических законах, лежащих в основе функционирования элементов систем. Эти характеристики отражают чисто математическую связь между входными и выходными величинами и не зависят от функционального назначения, принципа действия и конструктивного выполнения элементов системы. Поэтому такие характеристики для различных физических элементов (устройств) могут иметь одинаковый вид, что будет свидетельствовать об однотипности характера протекающих в них процессов.
АСР и АСУ состоят из связанных между собой функциональных элементов. Поэтому характеристики системы в целом можно получить из характеристик отдельных ее элементов.
Статическая характеристика устанавливает зависимость между входной Хвх и выходной Хвых величинами элементов и систем в установившемся состоянии равновесия:
Эта зависимость может быть линейной и нелинейной. Реальные статические характеристики в большинстве нелинейны. Однако, учитывая сравнительно небольшой диапазон величин, в которых обычно работают физические системы, часто можно представить их линейными характеристиками. При наличии существенной нелинейности статических характеристик приходится принимать меры конструктивного или схемного характера, линезирующие эти характеристики, иначе приходится учитывать нелинейность при расчетах АСР.
Динамическая характеристика показывает зависимость между выходной и входной величинами во времени:
Хвых f ( Хвх ,t ). |
(6.25) |
Они наиболее полно отображают свойства элементов системы и поэтому в дальнейшем используются в качестве основных характеристик при исследовании элементов и систем. Динамические характеристики в теории автоматического управления описываются дифференциальными уравнениями, передаточными функциями, временными и частотными характеристиками.
6.4.9.1. Дифференциальные уравнения для элементов системы
Вывод дифференциальных уравнений элементов системы - сложная творческая работа, при которой допускаются определенная идеализация процесса, пренебрежение отдельными факторами, рассмотрение частных случаев и т.д. Математические описания элементов и систем осуществляются на основе физических, электрических, химических, механических и др. законов, на которых основана работа элементов. Учитывая сложность математического описания динамики процессов в элементах, часто прибегают к упрощенным уравнениям, с помощью которых получают приближенные решения исходной задачи.
Анализ линейных систем существенно проще, чем анализ нелинейных систем. Поэтому часто применяют линеаризацию нелинейных уравнений, т.е. приведение нелинейных уравнений к линейным. Линеаризация основана на том, что в динамическом процессе автоматической системы все переменные изменяются так, что их отклонения от установившихся значений все время достаточно малы. Такое допущение справедливо, т.к. цель любой автомати-ческой системы состоит в том, чтобы не допустить отклонение регулируемой величины (а значит, и всех параметров) от заданного значения. Основная идея метода линеаризации заключается в разложении исходного уравнения в ряд Тейлора в окрестности некоторой базовой точки, соответствующей заданному значению регулируемой величины, и вычитании из полученного уравнения в приращениях уравнения для установившегося состояния. Таким образом, получают новое приближенное уравнение, которое отличается от исходного нелинейного тем, что
входящие в него переменные заменены их малыми приращениями.
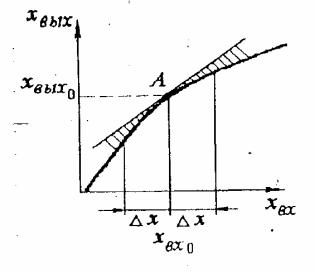
Геометрическая интерпретация метода линеаризации нелинейной функции хвых=f'(хвх) представлена на рис. 6.30.
Преобразование первоначальной нелинейной функции путем разложения в ряд Тейлора в окрестности точки А с координатами хвх0 и хвых0 и вычитания уравнения для
Рис. 6.30. Линеаризация нелинейности установившегося режима равносильно замене исходной кривой на касательную, проведенную через точку установившегося
режима.
При этом замена кривой на касательную всегда происходит с ошибкой (на рис. 6.30 заштрихована), величина которой увеличивается с увеличением отклонения аргумента от базового значения. Как видно, чем меньше ∆х, тем меньше ошибка линеаризации. С другой стороны возможность линеаризации тем шире, чем ближе линеаризуемая кривая к прямой. При невозможности линеаризации пользуются методом решения нелинейных уравнений.
Используя закон сохранения тепловой энергии и следующие допущения: объект регулирования считается сплошным однородным телом, обладающим бесконечно большой теплоемкостью; тепловая энергия, отдаваемая во внешнюю среду, пропорциональна разности температур объекта регулирования и окружающей среды; температура окружающей среды постоянна; теплоемкость и коэффициент теплоотдачи не зависят от температуры, можно составить следующее дифференциальное уравнение объекта регулирования:
где t - масса объекта, кг; С - удельная теплоемкость, Дж/кг.град; α -
коэффициент теплоотдачи, Вт/м2.град; F - площадь поверхности теплоотдачи, м2; Θ - превышение температуры над окружающей средой.
Приведем уравнение (6.26) к каноническому виду
|
|
|
|
|
|
|
T |
d |
K P(t), |
(6.27) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
где |
T |
m C |
; |
K |
max |
min |
; Θmax - установившееся значение темпера- |
|
Pmax |
|
|
|
F |
|
Pmin |
|
туры, соответствующее максимальной подводимой мощности Рmax; Θmin - установившееся значение температуры при минимальной подводимой мощности Рmin.
Приравняв производную нулю, что соответствует установившемуся режиму, из выражения (6.27) получим уравнение статической характеристики объекта регулирования:
Здесь входной величиной является мощность нагревателя Р, а выходной - температура Θ рабочей поверхности нагретого тела. Коэффициент К в выражении (6.28) называется коэффициентом передачи (усиления). Он
численно равен изменению выходной величины при изменении входной на единицу и может выражаться как в
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
размерном, так и в безразмерном виде. |
|
|
|
|
|
|
Реакция элемента (звена) системы |
|
|
|
|
|
автоматики на мгновенное скачко- |
|
|
|
|
|
образное |
изменение входной |
величины |
|
|
|
|
|
называется кривой разгона (рис. 6.31). |
|
|
|
|
|
|
Для |
большинства |
промышленных |
|
|
|
|
|
объектов |
реагирования |
выходная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величина |
начинает |
изменяться |
не |
|
|
|
|
|
одновременно с приложением регули- |
|
|
|
|
|
рующего (управляющего) воздействия, а |
|
|
|
|
|
спустя некоторый промежуток времени. К |
|
|
|
|
|
таким объектам относятся, например, |
|
|
|
|
|
трубопроводы, тепловые объекты (пресс- |
|
|
|
|
|
формы, прессы с обогревом, сушилки и |
|
|
|
|
|
|
|
|
|
|
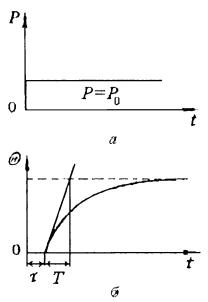
т.д.), процессы растворения и др. Время, |
|
|
|
|
|
численно |
равное времени |
отставания |
Рис. 6.31. Кривая разгона объекта |
реакции изменения выходной величины, |
с запаздыванием |
называется временем запаздывания τ, |
ко- |
|
|
|
|
|
торое остается постоянным в ходе всего |
технологического процесса (рис. 6.31, б).
При анализе АСР свойство запаздывания учитывается введением в его
структуру члена чистого запаздывания |
|
|
(t) P(t ). |
(6.29) |
С учетом запаздывания уравнение рассматриваемого объекта примет |
вид |
|
T |
d |
K P(t ). |
(6.30) |
|
|
dt |
|
Изменения выходной величины Θ(t) при нанесении скачкообразного входного воздействия Р=Р0 (рис. 6.31, а) описываются уравнением
Инерционные свойства такого объекта определяются постоянной времени Т и запаздыванием τ. В общем случае элементы и системы автомати-
ческого регулирования могут описываться линейными дифференциальными уравнениями с постоянными коэффициентами следующего вида:
|
dnxвых |
a |
dn 1xвых |
... a |
n 1 |
|
dtn |
dtn 1 |
|
1 |
|
dmxmвх b1 dm m1x1вх ... bm 1 dt dt
|
|
|
|
dxвых |
anxвых |
|
dt |
|
|
|
dxвх |
b x , |
(6.32) |
|
dt |
m вх |
|
|
|
при этом в реальных системах n > m.
6.4.9.2. Передаточные функции
При исследовании АСР широко используются прикладные математические методы операционного исчисления, существенно облегчающие задачу исследования сложных систем регулирования. В частности, в теории автоматического регулирования используют преобразование функции вещественного переменного (времени) в функцию комплексного переменного, называемое преобразованием Лапласа.
Преобразованием функции-оригинала х(t) называется функция х(р) комплексного переменного p α jω, определяемая интегралом Лапласа
|
|
x( p) x(t ) e p tdt. |
(6.33) |
0 |
|
Символически преобразование Лапласа изображается следующим образом: L[х(t)] = х(р). Применение преобразования Лапласа превращает дифференциальные уравнения в алгебраические, что упрощает дальнейшее решение задач по описанию и расчету систем регулирования.
Применив преобразование Лапласа к дифференциальному уравнению (6.32) при нулевых начальных условиях (при t = 0; х (t) = 0; х'(t) = 0 и т.д.), получим уравнение, записанное в операторном виде:
(ao pn a1pn 1 ... an 1p an )xвых( p)
(6.34)
(b0 pm b1pm 1 ... bm 1p bm )xвх( p).
На основе уравнения (6.34) получается выражение для передаточной функции:
|
x |
вых |
( p) |
|
b pm b pm 1 |
... b |
|
p b |
|
|
B( p) |
|
W( p) |
|
|
|
|
0 |
1 |
m 1 |
m |
|
|
. |
(6.35) |
x ( p) |
|
pn a pn 1 |
|
|
|
|
|
a |
o |
... a |
n 1 |
p a |
n |
A( p) |
|
|
|
вх |
|
|
|
|
1 |
|
|
|
|
|
Таким образом, передаточной функцией W(p) называется отношение преобразования Лапласа выходной величины к преобразованию Лапласа входной величины, найденных при нулевых начальных условиях.
Для быстрого определения W(p) по виду исходного дифференциального уравнения (6.32) существует формальное правило: необходимо предварительно заменить все производные на р в соответствующей степени, а
затем разделить правую часть уравнения на левую. Например, d2х/dt2 заменяется на р2, dх/dt - на р, х - на 1 и т.п.
6.4.9.3. Временные характеристики
Временная характеристика или кривая разгона при единичном входном воздействии называется переходной и ее обозначают h(t). Для аналитического нахождения временной характеристики надо решить дифференциальные уравнения для системы при ступенчатом входном воздействии.
Для обратного преобразования Лапласа в целях определения переходной функции можно воспользоваться формулой Хевисайда
h(t ) |
A(0) |
|
|
A( pK ) |
|
epK t , |
|
|
pK B'( pK ) |
(6.36) |
|
B(0) |
|
где pK - корни уравнения A(p) = 0.
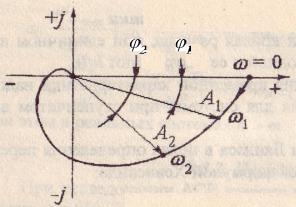
Рис.6.32. Амплитудно-фазовая (комплексная) частотная характеристика
амплитудное и фазовое значения:
6.4.9.4. Частотные характеристики
Если в выражении для передаточной функции вместо p поставить jω, то получим комплексную частотную характеристику W(jω), называемую амплитуднофазовой частотной характеристикой (АФХ) (рис. 6.32). Ее можно выразить через вещественную и мнимую составляющие, а также
W( j ) P( ) j Q( ) A( ) ej( ). |
(6.37) |
где Р(ω) и Q(ω) - соответственно вещественная и мнимая составляющие АФХ; A(ω) - амплитудно-частотная характеристика (АЧХ), показывающая относительное изменение амплитуд выходного сигнала по отношению к амплитуде входного сигнала от частоты ω входных колебаний; φ(ω) - фазочастотная характеристика (ФЧХ), показывающая зависимость фазы выходных сигналов от частоты ω входных колебаний.
Частотные характеристики можно получить и экспериментально: если на вход системы подать гармоническое воздействие xвх с частотой ω и амплитудой Авх, то через определенное время на выходе также установятся гармонические колебания с частотой ω, но с амплитудой сигнала Авых и сдвинутые по фазе на φ(ω).
Тогда для входных и выходных колебаний и их отношений справедливы следующие уравнения в комплексной форме:
x |
вх |
A |
|
e jωt |
; x |
вых |
A |
ej( t ); |
|
|
|
|
вх |
|
|
|
вых |
|
|
|
W( j |
|
) A |
|
/ |
A |
e j |
A( ) ej |
( ). |
(6.38) |
|
|
1 |
|
|
вых |
|
вх |
|
|
|
|
6.4.9.5. Типовые динамические звенья АСР
Звенья АСР могут иметь различные физические принципы действия, различные схемы и конструктивные формы, а также назначения. Однако с точки зрения динамических свойств звена имеют значения лишь уравнения, связывающие выходную и входную величины звена.
В классическом варианте выделяют обычно семь типовых звеньев: 1) безынерционное звено; 2) инерционное звено; 3) интегрирующее звено; 4) колебательное звено; 5) дифференцирующее звено; 6) упругое (интегродифференцирующее) звено; 7) запаздывающее звено.
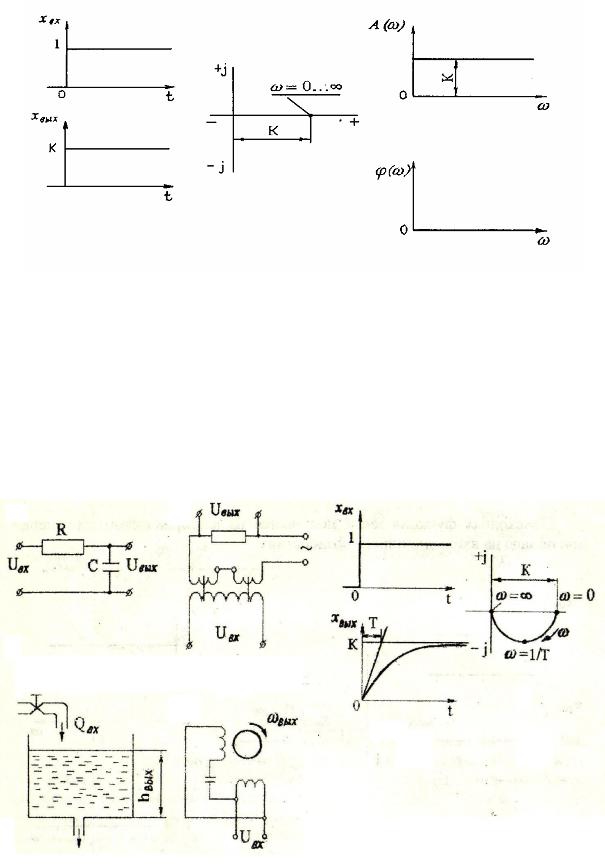
1. Безынерционное (статическое) звено.
Оно называется также пропорциональным или усилительным звеном и описывается простейшим алгебраическим уравнением
где К - коэффициент передачи.
Выходная величина этого звена пропорциональна входной величине.
Примеры такого звена показаны на рис. 6.33. Из (6.39) имеем
xвых( p ) K xвх( p ),
(6.40)
тогда передаточная функция будет
W( p) |
xвых( p ) |
K . |
(6.41) |
|
|
xвх( p) |
|
Переходная функция звена получается из алгебраического уравнения при подаче на вход единичного воздействия
Как видно, АФХ представляет собой точку на действительной оси комплексной плоскости, АЧХ постоянна для всех значений частот, а фазовый сдвиг равен нулю: φ(ω)=0.
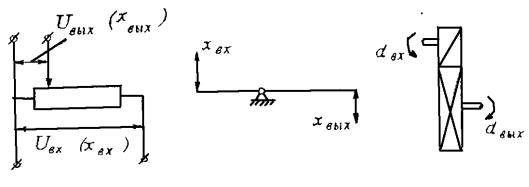
Рис. 6.33. Примеры безынерционного звена: а - потенциометр; б - рычаг; в - редуктор
в
г
Рис. 6.34. Характеристики безынерционного звена: а - переходная функция; б - АФХ; в - АЧХ; г - ФЧХ
2. Инерционное (апериодическое) звено описывается следующим дифференциальным уравнением первого порядка:
T |
dxвых |
xвых |
K xвх , |
(6.43) |
|
|
dt |
|
|
где Т - постоянная времени; К - коэффициент передачи.
Примеры систем, эквивалентных инерционному звену, представлены на рис. 6.35.
ав
а б
|
б |
|
г |
|
|
|
|
|
|
|
|
|
|
Рис. 6.35. Примеры |
Рис. 6.36. Переходная функция |
апериодического звена: а - RС-контур; 607 |
(а) и амплитудно-фазовая |
б - одноемкостный гидравлический |
характеристика (б) апериодического |
объект; в - магнитный усилитель; г - |
звена |
двухфазный асинхронный двигатель |
|