Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2023.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

2.62 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 197 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

			+ KB
x1	= KBT1 ln	x2		−T1 (x2	− x24 )+ x14 ,	(2.44)

	x24		+ KB

где начальные условия x14 и x24 определяются положением точки M4. x14 = b2, (2.45)

а x24 определяется по траектории (2.41) совместно с условием (2.42) и выражением (2.45):

b2 = −T1 (x24 − x23 )−b1 .

(2.46)

Искомая точка последовательности M5 определяется по траекто-
рии (2.44) при пересечении оси абсцисс, т.е. при x2 = x25 = 0.
	KB
x15 = KBT1 ln		−T1x24 +b2 .	(2.47)

x24	+ KB

(2.47) дает искомую функцию преобразованияДИx15 = f(x10).

Таким образом, система уравнений (2.37), (2.40), (2.43), (2.46) и

гармонического баланса Нб.М. КрыловаАи Н.Н. Боголюбова. Гармоническая линеаризац я является при лиженным методом исследования нелинейных систем пр меняется только в случае, когда линейная часть системы является ф льтром низких частот. Управляемые систе-

2.9. Гармоническая линеаризация нелинейностей

Гармоническая линеаризация нелинейностей основана на методе

мы, как правилоС, обладаютисвойством фильтра низких частот, т.е. при возникновении периодических несинусоидальных режимов они не пропускают или пропускают с большим ослаблением вторые и более высокие гармоники. При этом линейная часть может быть описана дифференциальным уравнением любого порядка, а нелинейный элемент может быть как однозначным, так и многозначным.

Суть гармонической линеаризации состоит в описании нелинейного звена линейным уравнением, которое получается при пренебрежении (отбрасывании) высшими гармониками в разложении нелинейной функции в ряд Фурье. Другими словами нелинейный элемент заменяется линейным звеном, параметры которого определяются при гармоническом входном воздействии из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена.

Согласно данному способу выбирается некоторая расчетная структурная схема, в которой нелинейный элемент НЭ выделен в качестве входного звена, а вся остальная линейная часть ЛЧ системы объединена в одну общую передаточную функцию, которая располагается после нелинейного элемента (рис. 2.12).

Прохождение синусоидального сигнала через нелинейную систему при входном воздействии u(t) = 0 показано на расчетноструктурной схеме (см. рис. 2.12).

x		z		y
x	НЭ	z	ЛЧ	y
	НЭ		ЛЧ

x(t)	z(t)					y(t)
					А	И
Рис. 2.12. Прохождение синусоидального сигнала через нелинейную систему
	б
	Пусть нелинейный элемент имеетДнелинейную функцию z = F(x).
Подадим на вход этого элемента гармонический сигнал x = Asinωt. На
	и
выходе получим z = F(Asinωt). Этот периодический выходной сигнал
нелинейного звена можно разложить в ряд Фурье:
	z = F(Asin ωt) =		A0		+∑(An cosnωt + Bn sin nωt),		(2.48)
	z = F(Asin ωt) =				+∑(An cosnωt + Bn sin nωt),		(2.48)
		2
где первая и последующие гармоники имеют выражение
	СA =		ω	2π/ω F (Asin ωt)dt ;			(2.49)
	0		π		∫
				0
	2π/ω
	An = ωπ	∫		F (Asin ωt)cosnωtdt ;			(2.50)
		0
	2π/ω
	Bn = ωπ	∫		F (Asin ωt)sin nωtdt .			(2.51)
		0

Следовательно, на линейную часть системы действует сигнал, содержащий весь спектр частот (после разложения их в ряд Фурье), которые возникли в нелинейном элементе. В силу принципа суперпо-

зиции в линейной части системы каждая гармоника действует независимо от остальных. Амплитуда каждой гармоники на выходе линейной части системы y(t) будет зависеть от динамических свойств этой линейной части. Предположим, что наша система обладает тем свойством, что величина амплитудной характеристики на частотах высших гармоник значительно меньше, чем первой:

	WЛЧ ( jωn)		<<		WЛЧ ( jω)		.	(2.52)

Это свойство называется свойством фильтра низких частот

линейной части системы. При наличии свойства фильтра линейная часть системы будет хорошо пропускать первую гармонику нелинейных колебаний y(t) и ослаблять все высшие гармоники. Поэтому на выходе системы рассматривается только первая гармоника. На рис. 2.12 эта первая гармоника на графике y(t) показана жирной линией. Данный сигнал по обратной связи приходит на вход нелинейного элемента, поэтому переменная x на входе нелинейного звена окажется близкой к синусоиде x = Asinωt.

Согласно формуле (2.48) запишем уравнение первой гармоники
	A0		И
z =	A0	+ A cosωt + B sin ωt .		(2.53)
z =		+ A cosωt + B sin ωt .		(2.53)
	2	1	1
	2		Д
			Д	относительно
При симметричных гармонических колебаниях				относительно

оси абсцисс составляющая уравнения (2.53) А0 = 0. Тогда уравнение
(2.50) можно записать в в де		А
(2.50) можно записать в в де
			′		(2.54)
	z = q(бA)Asin ωt +q (A)Acosωt ,				(2.54)
где коэффициенты	и
	и		B1 ;
С		q(A) =	B1 ;		(2.55)
			A
			А1
		′	А1
		′	А .		(2.56)
		q (А) =	А .		(2.56)
Подставив x = Asinωt и x' = Aωcosωt в уравнение (2.54), получим
выражение в операторной форме
			′	px
			′	ω .	(2.57)
	z = q(A)x +q (A)			ω .	(2.57)

Данное уравнение называют уравнением гармонической линеаризации, а коэффициенты q(A) и q'(A) – коэффициентами гармони-

ческой линеаризации, определяемыми выражениями:

	1	2π
q(A)=		∫F (Asin ϕ)sin ϕdϕ;	(2.58)
	πА
		0
	1	2π
q′(A)=		∫F (Asin ϕ)cosϕdϕ;	(2.59)
	πА
		0	(2.60)
		ϕ = ωt .

Правая часть выражения (2.57) линейна при постоянной амплитуде сигнала A = const, т.е. справедлива только для конкретного периодического решения. Но в целом она сохраняет нелинейные свойства, так как коэффициенты данного периодического решения q(A) и q'(A) от величины амплитуды колебаний х(t). Эта особенность гармонической линеаризации позволит исследовать основные свойства и особенности процессов в нелинейных автоматических системах.

Гармонической передаточной функцией (ГПФ) нелинейного элемента называется отношение амплитуды первой гармоники выходного сигнала к амплитуде входного сигнала. ГПФ нелинейного

нелинейности F(x) зав с т только от амплитуды A и не зависит от частоты сигнала ω, в отличие от характеристик линейных звеньев.

звена имеет общий вид			z( p)					И
								И
WНЭ ( p)		=						′	p	.	(2.61)
								′
			x( p)		= q(A) + q (A)				ω
			x( p)			Д			ω
						Д
Частотная ГПФ (комплексный коэффициент передачи) линеа-
ризованного нелинейного звена при подстановке p = jω имеет вид
WНЭ				А			′				(2.62)
WНЭ		( jA) = q(A) + jq						(A) .			(2.62)
	б
Следовательно, ампл тудно-фазовая частотная характеристика
и
С

Гармоническую линеаризацию еще называют амплитудной интерполяцией, так как она характеризует зависимость амплитуды выходного сигнала от амплитуды входного сигнала и не зависит от и з- менения частоты входного сигнала. Для большинства инженерных расчетов способ дает достаточно адекватный результат.

Следует иметь в виду, что гармоническая линеаризация является приближенным описанием нелинейной характеристики, полученной по изменению первой гармоники ряда Фурье. При этом количественно не оцениваются погрешности в результате отбрасывания высших гармоник. Но можно утверждать, чем выше порядок линейной части системы, тем более строго выполняется гипотеза фильтра низких частот и тем большую адекватность имеют методы исследования, использующие гармоническую линеаризацию.

Вычисление коэффициентов гармонической линеаризации. Если характеристика нелинейного элемента является однозначной и симметричной относительно начала координат, то функция F(Asinωt) будет нечётной. В этом случае, согласно формуле (2.59), мнимый коэффициент гармонической линеаризации q'(A) = 0, т.е. при отсутствии гистерезиса в характеристике нелинейного элемента (однозначная характеристика), она заменяется коэффициентом передачи, зависящим от амплитуды входного сигнала q(A).

Гистерезисная же петля вводит, согласно (2.54), производную входной величины нелинейного элемента. Так как q'(A) < 0, то экв и- валентное линейное звено, полученное после линеаризации гистерезисной релейной характеристики, дает отставание сигнала по фазе. Однако можно спроектировать специальное нелинейное звено с опе-

Вслучаях, когда нелинейное звеноДописываетсяИ сложным уравнением, включающим сумму различныхАлинейных и нелинейных выражений, каждый из нелинейных членов подвергается гармонической линеаризации по отдельностиб. Произведение же нелинейностей рассматривается обязательно в целом, как одна сложная нелинейность. При этом могут встретитьсяииного характера нелинейные функции.

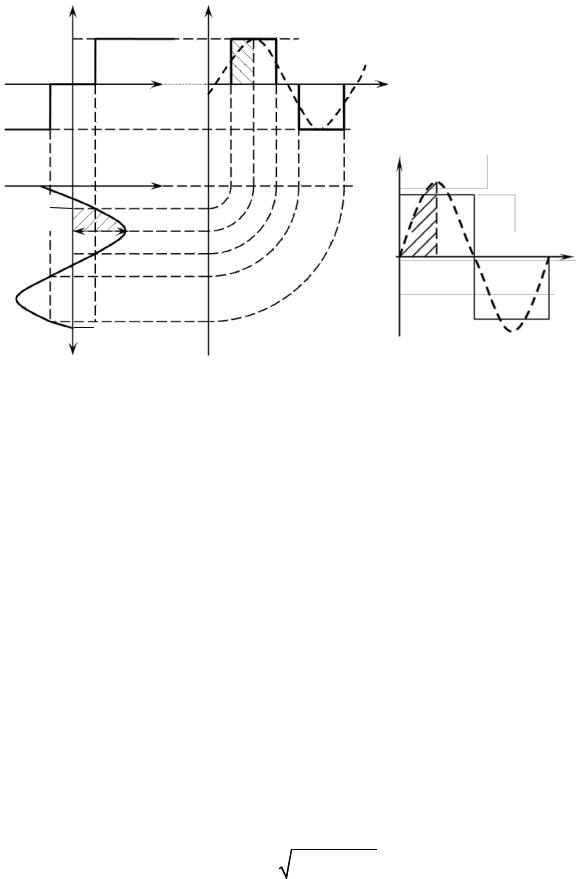
Вкачестве пр мера рассмотрим линеаризацию нелинейного элемента с характерСст кой «Идеальное трехпозиционное реле» (см. табл. 1.1, п. 7). Пусть на вход нелинейного звена (рис. 2.13, а) подан синусоидальный сигнал (рис. 2.13, б). На выходе релейного элемента возникает последовательность прямоугольных импульсов (рис. 2.13, в). Высота импульсов соответствует выходной величине реле. Частота следования импульсов полностью совпадает с частотой входного синусоидального сигнала. Ширина импульса зависит от амплитуды входного сигнала A. С увеличением амплитуды A ширина импульсов увеличивается.

Учитывая, что петли гистерезиса в характеристике нет, то коэффициент гармонической линеаризации q'(A) = 0. Тогда уравнение гармонической линеаризации имеет вид

z = q(A)x = x	1	2∫πF(Asin ϕ)sin ϕdϕ.	(2.63)
z = q(A)x = x		2∫πF(Asin ϕ)sin ϕdϕ.	(2.63)
	πА 0
			50

		z			zвых
а B					в
	–b			x
			b	x	ωt

		–B
					zвых	г
				xвх	zвых

	ωt1
	ωt1
б					π	2π
б					0 π/2	ωt
					0 π/2	ωt

ωt 2π

больше зоны нечувствительности Asinωt ≥ b. На участке от 0 до ωt

Рис. 2.13. Определение коэффициентов гармонической линеаризации
	И
На рис. 2.13, б видно, что реле срабатывает при входном сигнале
Д
А

чен, то можно измен ть пределы интегрирования для упрощения взятия интеграла.

б 1 1

выходного сигнала нет. Следовательно, интегрирование надо осуществлять с момента ωиt1. Поскольку выходной сигнал с реле симметри-

на. Затем результатСнадо умножить на четыре, чтобы получить значение импульсов от всей синусоиды от ωt = 0 до ω t = 2π. Определяем коэффициент q(A):

Интегрирован е будет выполняться в пределах от ωt1 до π/2. Эта часть входного и выходного сигналов на рис. 2.13, б и в заштрихова-

		1	2π			4	π/2
q(A) =		1	∫F (Asin ϕ)sin ϕdϕ =			4	∫ Bsin ωtdωt ;	(2.64)
q(A) =		πA	∫F (Asin ϕ)sin ϕdϕ =			πA	∫ Bsin ωtdωt ;	(2.64)
		πA	0			πA	ωt
							1
	q(A) = −			4B	[−cosωt]π/2 =	4B cosωt1.		(2.65)
				πA	ωt1	πA

В полученном уравнении выразим cosωt1 через sinωt1:

q(A) = 4B
q(A) = 4B	1−sin2 ωt .	(2.66)
πA	1
πA
		51

Значение sinωt1 связано с амплитудой входного сигнала А и зоной нечувствительности реле b следующим соотношением:

sin ωt

(2.67)

Таким образом, с учетом (2.67) коэффициент гармонической ли-

неаризации

q(A) =

−b

−

(2.68)

πA

ГПФ нелинейного звена «Идеальное трехпозиционное реле» представляет собой идеальное усилительное звено, коэффициент ко-

торого зависит от амплитуды колебаний:
		z( p)		4B
W	( p) =		=		A2 −b2 .	(2.69)

НЭ		x( p)		πA2

нелинейного элемента с характеристикой «ИИдеальное двухпозиционное реле» (см. табл. 1.1, п. 6). Выходной сигнал будет иметь вид, по-

казанный на рис. 2.13, г. После аппроксимацииД выходного сигнала первым членом ряда Фурье в виде амплитуды выходного сигнала по-

Рассмотрим получение гармонической передаточной функции

лучаем пределы измерения четверти выходной синусоиды от ωt = 0 до

ωt = π/2. Эта часть синусоиды заштрихована. Тогда коэффициент гар-

монической линеар

зац

q(A) определяется как

2π

π/2

q(A) =

∫F (Asin ϕ)sin ϕdϕ =

∫ Bsin ωtdωt ;

(2.70)

πA

и0

q(A) = −4B [−cosωt]π/2

= 4B .

(2.71)

πA

ГПФ «Идеального двухпозиционного реле» имеет вид

W ( p) =

z( p)

= 4B .

(2.72)

НЭ

x( p)

πA

В качестве примера рассмотрим линеаризацию нелинейного элемента с релейной характеристикой «Двухпозиционное реле с гистерезисом» (см. табл. 1.1, п. 8) (рис. 2.14). При гистерезисной характеристике релейного элемента ГПФ зависит от изменения выходного сигнала по возрастающей и по спадающей ветви характеристики.

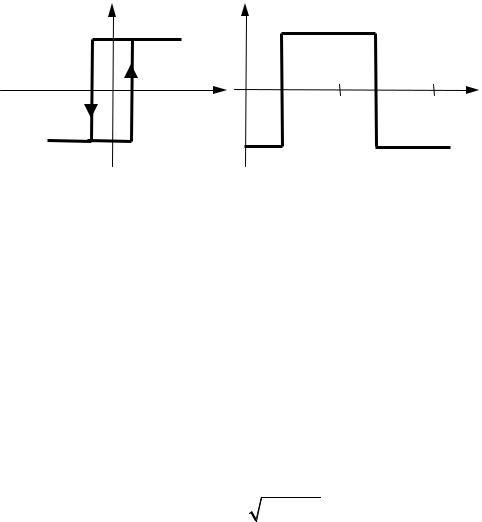
Переключение реле происходит при равенстве входной величины реле порогу его срабатывания x = b. Поэтому в момент переключения величина sinφ1 определяется выражением Asinφ1 = b. Очевидно, что для срабатывания реле необходимо, чтобы Asinφ1 ≥ b.

Z		+B	F(Asinφ)
B		+B
B
–b	b	X 0	φ1	π	2π φ
0	b	X 0	φ1	π	2π φ
	–B	-B		И
				И
Рис. 2.14. Определение коэффициента гармонической линеаризации

Коэффициент q(A) определяется по формуле (2.58), как и (2.64), только интегрирование будет выполняться в пределах от 0 до π с удвоением результата:

	1	2π	2B	ωt1		π
q(A) =		∫F (Asin ϕ)sin ϕdϕ =		∫	−sin ωtdωt + ∫sin ωtdωt		; (2.73)
q(A) =	πA	∫F (Asin ϕ)sin ϕdϕ =		∫	−sin ωtdωt + ∫sin ωtdωt		; (2.73)
	πA	0	πA	0	Д	ωt
						1

q(A) =

cosωt

ωt1

−cosωt

cosωt .

(2.74)

πA

ωt1

πA

В полученном уравненбвыразим cosωt1 через sinωt1

и с учетом

sinωt1 = b/A, как и в формулах (2.66) – (2.68), запишем

q(A) =

A2 −b2

(2.75)

πA

Коэффициент q'(A) определяется по формуле (2.59):

1 2π

2B ωt1

′

∫F (Asin ϕ)cosϕdϕ =

∫ −cosωtdωt + ∫cosωtdωt ; (2.76)

q (A) =

πA

ωt

′

−sin ωt

ωt1

+sin ωt

= −

sin ωt1.

(2.77)

q (A) =

πA

ωt1

πA

Полученное уравнение с учетом sinωt1 = b/A запишем как

′

4Bb

(2.78)

q (A) = − πA2 .

Частотная передаточная функция «Двухпозиционного реле с

гистерезисом» имеет вид

( jA) = 4B

A2 −b2

− j 4Bb .

(2.79)

НЭ

πA2

Модуль ГПФ «Двухпозиционное реле с гистерезисом» совпада-

ет с соответствующим выражением для идеального реле:

WНЭ (

jА)

q(A)

+ q′(A)

= 4B .

(2.80)

πA

Фазовый сдвиг для петлевой релейной характеристики опреде-

ляется как

ϕНЭ(А)= arctg q′(A) = −arctg

(2.81)

q(A)

A2 −b2

В табл. 2.2 представлены коэффициенты гармонической линеа-

ризации для типовых нелинейностей.

Таблица 2.2

Коэффициенты гармонической линеаризации типовых нелинейностей

№ п/п Внешний вид характеристики

ДНазвание и коэффициенты звена

Зона нечувствительности

–b

arctg(k)

q(A)=

−arcsin

−b

− 2

;

′

при A ≥ b

q (A)= 0

Насыщение (ограничение)

q(A)

−b

;

–b

arcsin

πb

q′(A)= 0

при A ≥ b

–B

Зона нечувствительности

с насыщением

q(A)=

arcsin 2 −arcsin

–b2

–b1

π(b2 −b1 )

0 b1

+ 22

−b2

− 12

−b1

;

–B

′

при A ≥ b2

q (A)= 0

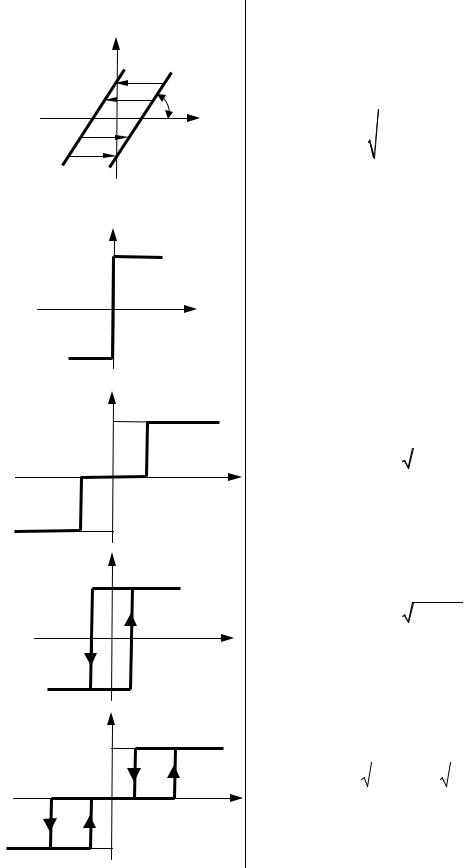
Окончание табл. 2.2

Люфт (Мертвый ход)

q(A)

+arcsin

−

arctg(k)

–b

−

;

4kb

q′(A)= −

при A ≥ b

−

πA

Идеальное двухпозиционное реле

q(A)=

;

πA

q′(A)= 0

–B

ДИдеальное трехпозиционное реле

q(A)=

;

–b

A2 −b2

πA2

q′(A)= 0 при A ≥ b

Двухпозиционное реле с гистерезисом

q(A)=

;

–b

A2 −b2

q′(A)= −

4Bb

при A ≥ b

–B

πA

Трехпозиционное реле с гистерезисом

;

–b2 –b1

q(A)=

[

−b2

−b1

]

πA2

0 b1

′

2B(b2 −b1 )

при A ≥ b2

πA2

–B

q (A)= −

2.10.Алгебраический метод определения автоколебаний

внелинейных системах

Данный метод предложил советский ученый Е.П. Попов. Рассмотрим определение симметричных автоколебаний алгебраическим методом на основе гармонической линеаризации нелинейности. Пусть автоматическая система (см. рис. 2.6) с одной нелинейностью F(x) имеет передаточную функцию линейной части, обладающую свойством фильтра низких частот:

WЛЧ (p)=

R(p)

(2.82)

Q(p)

Уравнения линейной части системы и нелинейного звена при

входном воздействии u(t) = 0 в операторной форме:

Q(p)y = R(p)z;

(2.83)

z = F(x) = −F(y).

Тогда уравнение замкнутой системы в операторной форме

примет вид

Q(p)y = −R

(p)F(y).

(2.84)

Возможные автоколе ания выходной величины с частотой ω' и

амплитудой А' запишем как

′

(2.85)

y = А sin ω t .

После гармон ческой л неаризации нелинейного элемента его

уравнение в операторной форме имеет вид

′

y ,

(2.86)

z = − q(A) +q (A)

где коэффициенты гармонической линеаризации q(A) и q'(A) определяются согласно формулам (2.75) и (2.78).

Тогда уравнение замкнутой системы (2.84) с учетом уравнения

(2.86) в операторной форме примет вид
	′		p	у = 0.	(2.87)

Q(p)+R(p) q(A) +q		(A)
			ω

Поскольку в искомом решении уравнения (2.85) А' = const и ω' = const, то гармонически линеаризованное уравнение замкнутой системы (2.87) можно рассматривать как обыкновенное линейное

уравнение с постоянными коэффициентами. Специфика его состоит лишь в том, что имеются неизвестные постоянные коэффициенты, зависящие от искомого решения, что и позволит нам получить решение со специфическими свойствами, присущими нелинейной системе.

Запишем характеристическое уравнение гармонически линеаризованной системы

	′	p	= 0 .	(2.88)

Q(p)+R(p) q(A) +q (A)
		ω

Периодическое решение (2.85) уравнения (2.87) соответствует паре чисто мнимых корней p1,2 = ± jω характеристического уравнения (2.88). Поэтому для отыскания этого решения перейдем в частотную

область, заменив оператор p = jω. Получим		И
	Q(jω)+R(jω)(q(A) + jq (A))= 0.		(2.89)
	′
	Выделим в этом выражении вещественную и мнимую части в
виде	Д
	U (A,ω)+ jV (A,ω)= 0.		(2.90)
	А
	В результате получим два алгебраических уравнения, из кото-

рых и определяются искомые амплитуда А' и частота ω' периодиче-
ского решения (2.85).	б
ского решения (2.85).
	U (A,ω)= 0;	(2.91)
	V (A,ω)= 0.	(2.91)

Заметим, что решен е задачи упрощается в случае однозначной
нелинейности F(x) (q'и(A) = 0), вместо уравнения (2.88) здесь имеем
Q(p)+R(p)q(A) = 0 .			(2.92)
При подстановкеСp = jω выделим вещественные и мнимые части
многочленов Q(p) и R(p) в виде
Q(jω)=UQ (ω)+ jVQ (ω);			(2.93)
R(jω)=U R (ω)+ jVR (ω).

Тогда вместо (2.91) получим
UQ (ω)+U R (ω)q(A) = 0;			(2.94)
V (ω)+V	R	(ω)q(A) = 0.
Q

Эти два уравнения можно преобразовать к виду

			UQ (ω)
q(A) = −				;
q(A) = −			U R (ω)	;				(2.95)
		(ω)V	U R (ω)			(ω)V		(2.95)
U		(ω)V	(ω)−U		Q	(ω)V	R	(ω)= 0.
	R	Q			Q		R

Сначала из второго уравнения определяется частота ω' периодического решения, а затем из первого уравнения определяется амплитуда А'. Видно, что частота зависит от параметров линейной части и не зависит от формы однозначной нелинейности. В случае гистерезисной нелинейности это свойство нарушается, и будет иметь место общий случай уравнений (2.91).

Определение устойчивости или неустойчивости найденного периодического решения будет рассматриваться в пункте 2.11 данного раздела. Если периодическое решение устойчиво, то в нелинейной АСУ имеется устойчивый автоколебательный процесс.

В качестве примера рассмотрим алгебраический метод для нелинейной системы (см. рис. 2.6) с типовой нелинейной характеристи-

кой «Насыщение» (см. табл. 1.1, п. 2) и «				вухпозиционное реле с гис-
терезисом» (см. табл. 1.1, п. 8).	А			И
Пусть уравнение динамики устройства управления УУ
б p					(2.96)
(T p +1)ϕ =ДK z ,
1			1
а уравнение динамики о ъекта управления ОУ будет
и		K2ϕ
(T p +1)y =				.	(2.97)
2

Уравнение нелинейного элемента НЭ при u(t) = 0 описывается нелинейной функцией «Насыщение» (см. табл. 1.1, п. 2).

Уравнение замкнутой системы в операторной форме при u(t) = 0
с учетом формулыС(2.17) будет иметь вид
(T1 p +1)(T2 p +1) py = −K1K2F (y).	(2.98)
После гармонической линеаризации нелинейного	элемента
«Насыщение» его уравнение в операторной форме имеет вид
z = −q(A)y ,	(2.99)

где коэффициент гармонической линеаризации q(A) определяется согласно табл. 2.1, а коэффициент q' (A) = 0.

Запишем характеристическое уравнение гармонически линеаризованной системы

T T p3		+(T +T ) p2		+ p + K K		q(A)= 0 .	(2.100)
1	2	1	2	1	2

При подстановке p = jω выделим согласно выражению (2.90) вещественные и мнимые части характеристического уравнения гармонически линеаризованной системы и получим по формулам (2.91) и (2.94)

			−(T1 +T2 )ω	2	= 0;
U (A,ω)= K1K2q(A)			−(T1 +T2 )ω		= 0;	(2.101)
		3				(2.101)
	ω	3	= 0.
V (A,ω)= ω−T1T2	ω		= 0.

Из второго уравнения (2.101) определяем частоту периодического решения

ω′ =	1						,				(2.102)

		T T
			1		2					И
подставляем полученное выражение в первое уравнение (2.101) и
получаем				Д

q(A′) =	T1				+T2				.		(2.103)
	K K T T
А								2
	1				2	1

Амплитуда автоколебаний ' определяется расчетным путем по

формуле коэффициента гармонической линеаризации нелинейного
		б
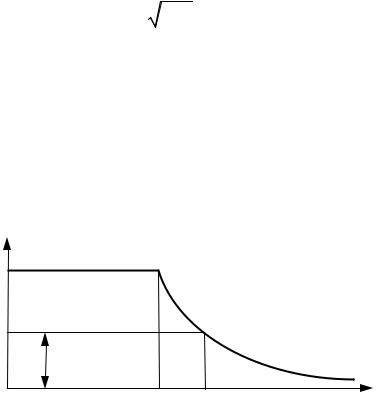
элемента «Насыщение» (см. та л. 2.1) или графически (рис. 2.15).
q(A)	и
q(A)
k
		T1 +T2
		K1K2T1T2
С0			b	A'	A

Рис. 2.15. Определение амплитуды автоколебаний А'

Если учесть, что коэффициент усиления «Насыщения» k ≥ q(A) (см. рис. 2.15), из уравнения (2.103) вытекают условия существования автоколебаний в системе:

kK K	2	> T1 +T2 ;	(2.104)
1	2	T1T2
		T1T2
KРАЗ		= kK1K2 ;	(2.105)
			59

k =	B	,	(2.106)
	b

где KРАЗ – общий коэффициент усиления разомкнутой цепи данной системы в линейном плане.

Легко видеть, что формула (2.104) представляет собой условие неустойчивости этой системы как линейной согласно критерию Гурвица, где граница устойчивости

KРАЗ = T1 +T2 =	1	+	1	(2.107)
			T2
T1T2	T1

является в то же время границей области автоколебаний.

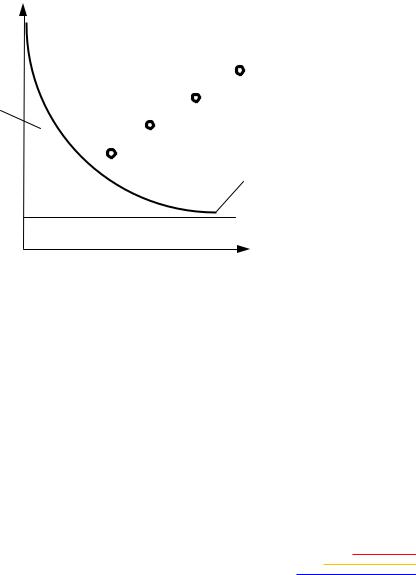
Эта граница нанесена штрихпунктирной линией на плоскости параметров [KРАЗ;T1] при T2 = const (рис. 2.16). Ниже этой границы имеет место область устойчивости равновесного состояния системы, а

выше – область автоколебаний, где согласно выражениям (2.102) и

А' и ω'.

(2.103) имеется бесконечное множество значений

KРАЗ

A'4

Область

A'3

ω'4

A'2

ω'4

устойчивости

A'1 ω'2

ω'1

KРАЗ = T

+ T

Рис. 2.16. Область устойчивости и автоколебаний

Для той же нелинейной системы (см. рис. 2.6) после гармонической линеаризации нелинейного элемента «Двухпозиционное реле с гистерезисом» его уравнение в операторной форме имеет вид

	′	p
			y ,	(2.108)
z = − q(A) +q (A)
		ω

где коэффициенты гармонической линеаризации q(A) и q'(A) определяются согласно формулам (2.75) и (2.78).

Запишем характеристическое уравнение гармонически линеаризованной системы с «Двухпозиционным реле с гистерезисом»

T1T2 p	3	+(T1 +T2 ) p	2		′	p	= 0. (2.109)

				+ p + K1K2 q(A) +q (A)
						ω


U (A,ω)= K1K2q(A)
	′

V (A,ω)= K1K2q (A)

−(T	+T	)ω2	= 0;
1	2			(2.110)
+ω−T T ω3			= 0.	(2.110)
+ω−T T ω3			= 0.
	1	2

Поделив первое уравнение системы на второе с учетом выраже-

ний (2.75) и (2.78), получим связь амплитуды А' и частоты периодиче-

ского решения ω':

q(A)

(T1 +T2 )ω′2

= −

q′(A)

ω′−T1T2ω′3

;

(2.111)

A′

−b

= (T1

+T2 )ω′.

(2.112)

1−T1T2ω′2

Данное уравнение накладывает ограничение на частоту перио-

дического решения:

′

ω <

(2.113)

бT1T2

Выразим амплитуду А' через частоту ω':

(T1 +T2 )ω′

′

b .

(2.114)

(1−T1T2ω′2 )

Из второго уравнения системы с учетом формулы (2.78) получим связь коэффициента усиления линейной части системы K1K2 с амплитудой А' и частотой периодического решения ω':

K1K2	=	πA′2	(ω′−T1T2ω′3 ).	(2.115)
		4Bb

Решив уравнение (2.115) с учетом формул (2.114) и (2.113) при T1 = T2 = 0,1; B = 25; b = 0,5 построим зависимость K1K2(А'; ω'), изображенную на рис. 2.17.

<<< < Предыдущая 1 2 3 4 5 67 / 197 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20212.61 Mб252018.pdf
#
07.01.20212.62 Mб182019.pdf
#
07.01.2021346.19 Кб3202.pdf
#
07.01.20212.62 Mб562020.pdf
#
07.01.20212.62 Mб72021.pdf
#
07.01.20212.62 Mб852023.pdf
#
07.01.20212.63 Mб22024.pdf
#
07.01.20212.65 Mб52025.pdf
#
07.01.20212.66 Mб22026.pdf
#
07.01.20212.66 Mб172027.pdf
#
07.01.20212.68 Mб32028.pdf