При гармонической линеаризации интервал значений 0 ≤ q(A) ≤ ∞ в действительности имеет место только для идеального реле. Для нелинейной характеристики, лежащей в интервале угла, значение q(A) заключено в пределах

В таком случае дополнительную область устойчивости определяют в зависимости от максимального и минимального значений коэффициента гармонической линеаризации для каждого вида нелинейной характеристики.

Вначале границу области абсолютной устойчивости определяют при 0 ≤ q(A) ≤ ∞ согласно (2.191). Это решение дает достаточные усло-

ческой линеаризации. Затем получают дополнительную область ус-

вия устойчивости при любой форме однозначной нелинейной характеристики и при любом интервале измененияИкоэффициента гармони-

тойчивости за счёт ограничения интервалаДфактически возможного

изменения коэффициента гармонической линеаризации (учет границ

нелинейности). Для этого в уравнения (2.191) надо подставить значе-

и достаточные условия устойчивостиАпри заданной форме однозначной нелинейной характеристикии . Кроме этого, по условию (2.189) при различных варьируемых параметрах линейной части можно определить область устойчСвого автоколебательного режима (см. рис. 2.16).

ния q(A)min и q(A)max. Чем более узкий сектор, где разместилась вся не-

линейная характеристика, тем больше будет область дополнительной границы абсолютной устойчивостиб. Такое решение дает необходимые

2.16. Анализ одночастотных вынужденных колебаний

Исследование вынужденных колебаний нелинейных систем представляет собой в общем сложную задачу в связи с отсутствием суперпозиции отдельных решений, а также существенным изменением поведения системы в зависимости от размера амплитуды колебаний, с наличием не единственного установившегося режима и возможностью перескоков с одного режима на другой, с особенностями высших гармоник, субгармоник, комбинационных частот и с многими другими факторами.

Рассмотрим случай одночастотных вынужденных колебаний, т.е. колебаний нелинейной системы с частотой внешнего периодического воздействия, и найдем условия их существования.

92

Форма колебаний, как и прежде, на основании свойства фильтра линейной части системы будет считаться близкой к синусоидальной для переменной х, стоящей под знаком нелинейной функции. При рассмотрении вынужденных колебаний во многих случаях возникают ограничения, накладываемые на амплитуду и частоту внешнего периодического воздействия (зависящие также и от параметров системы) и обусловливающие существование одночастотных вынужденных колебаний в нелинейной системе. Будем их кратко называть условиями захватывания (в указанном широком смысле). Особое значение эти условия приобретают для автоколебательных систем при частотах, близких к частоте автоколебаний и выше.

Пусть нелинейная АСУ (см. рис. 1.1) с одной нелинейностью

где коэффициенты гармонической линеаризации q(A) и q'(A) определяются согласно формулам (2.75) и (2.78).

93

Тогда уравнение замкнутой системы (2.205) с учетом формул

(2.203), (2.206) и (2.207) примет вид:

Для отыскания периодического решения вынужденных колебаний выходной величины используем символический метод определения, перейдя в частотную область и заменив p = jω', а вместо sinω't подставив выражение ejω't. Тогда получим

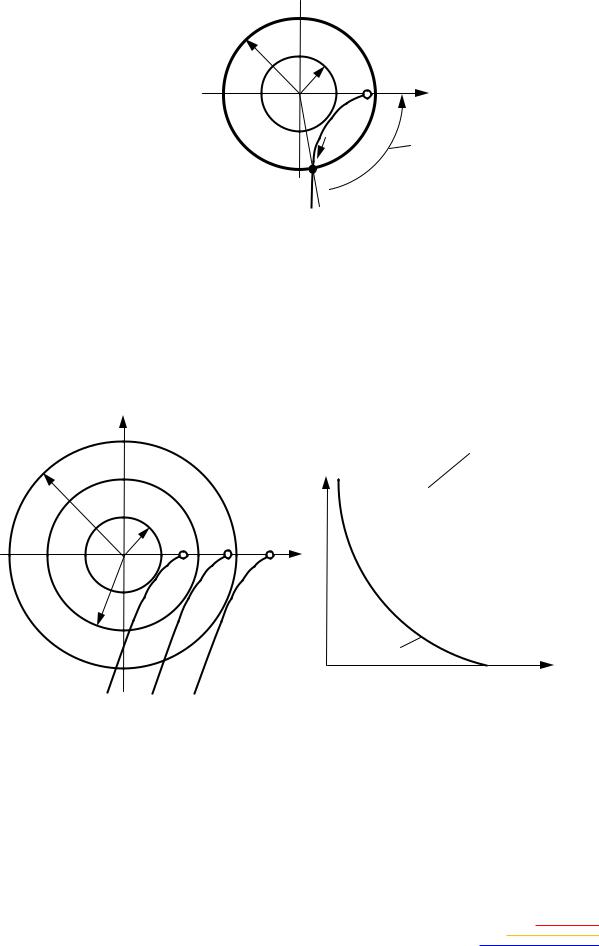
Уравнение (2.211) с двумя неизвестными А' и φ' можно решить графически, как показано на рис. 2.38. Правая часть (2.211) изображается на комплексной плоскости [+1; j] в виде окружности радиуса В, а левая часть Z(A) строится как кривая по точкам при постоянной частоте ω' и различных значениях амплитуды А. Точки пересечения окружности с кривой Z(A) дают периодическое решение, причем величина амплитуды вынужденных колебаний определяется в точке пересечения по кривой Z(A), а фаза – по величине угла φ' (см. рис. 2.38).

На рис. 2.38 окружность пересекает кривую Z(A) только при радиусе, большем некоторого порогового значения В > Вкр. Следовательно, в этом случае одночастотные вынужденные колебания (2.206) возможны только при достаточно большой амплитуде В, а при меньшей амплитуде В внешнего воздействия будет иметь место сложное движение, включающее в себя и собственную частоту системы.

94

jV(ω)

ВВкр

Z(A)

Рис. 2.38. Графическое определение параметров вынужденных колебаний

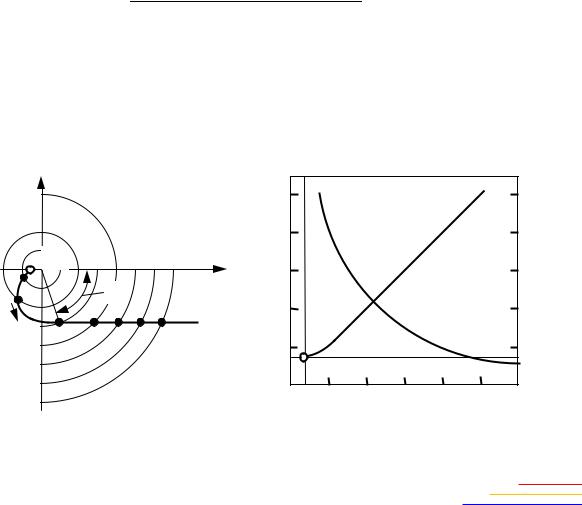
Построив серию кривых Z(A) по формуле (2.211) для разных значений частоты внешнего гармонического воздействия ω' (рис. 2.39, а),

Рис. 2.39. Определение области захватывания

Явление захватывания состоит в том, что при В > Вкр собственные колебания (автоколебания) срываются и система переходит целиком на одночастотные вынужденные колебания с частотой внешнего воздействия ω'. Данные одночастотные вынужденные колебания в соответствии со свойством фильтра низких частот линейной части системы для переменной х будут только близки к синусоидальным.

95

96