2.14. Прямой метод Ляпунова

Данный метод А.М. Ляпунова, являющийся также вторым методом, основан на построении специальных функций (функций Ляпунова) по исходным нелинейным дифференциальным уравнениям, описывающим поведение системы. Данные скалярные функции, характеризуют динамические свойства нелинейной системы и позволяют сделать вывод о её устойчивости.

В общем случае свободное движение нелинейной динамической системы описывается системой дифференциальных уравнений состояния 1-го порядка в форме Коши. Напомним, что данные уравнения получаются путём введения в исходное уравнение системы новых переменных состояния xi(t) вместо (i – 1) производных выходной величины y(t):

ФункциейСЛяпунова называется некоторая скалярная функция координат состояния V(x1; x2;…xn), которая принимает вещественные значения и удовлетворяет следующим свойствам:

1)функция однозначная;

2)V{0} = 0;

3)непрерывная вместе со своими частными производными в об-

ласти |xi(t)| ≤ H, где H –некоторая положительная постоянная. Функция Ляпунова V{x} называется знакоопределенной (опре-

деленно-положительной или определенно-отрицательной), если в области |xi(t)| ≤ H она принимает значение только одного знака и обращается в нуль только в начале координат. Например,

81

•определенно-положительная функция V = x12 + x22 + x32 ;

•определенно-отрицательная функция V = −(x12 + x22 + x32 ).

Данные функции равны нулю только при x1 = x2 = x3= 0. Функция Ляпунова V{x} называется знакопостоянной (положи-

тельной или отрицательной), если в области |xi(t)| ≤ H она принимает значения только одного знака и обращается в нуль в конечном числе точек заданной области фазового пространства. Например:

•V = (x1 − x2 )2 , V{x} = 0 при x1 = x2, в том числе и при x1 = x2= 0;

•V = (x1 − x2 )2 + x32 . V{x} = 0 при x1 = x2 и при x3= 0.

Функция Ляпунова V{x} называется знакопеременной, если в об-

нейных и нелинейных систем получила функция Ляпунова в виде квадратичной формы (квадратичная функция)

Используемая при записи квадратичной формы матрица является симметричной, в ней элементы симметричны относительно главной диагонали, т.е.

Квадратичная форма функции Ляпунова (2.162) по критерию Сильвестра будет определенно-положительной, если каждый из ее главных диагональных миноров будет положительным:

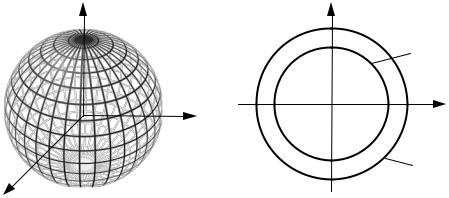
В фазовом пространстве постоянному значению простейшей квадратичной функции Ляпунова (V{x} = const) соответствует поверхность при n = 3 или плоскость при n = 2 (рис. 2.34).

Используя равенства (2.159), можно записать полную производ-

ную функции Ляпунова по времени, являющуюся общей функцией для системы и функции Ляпунова V{x}:

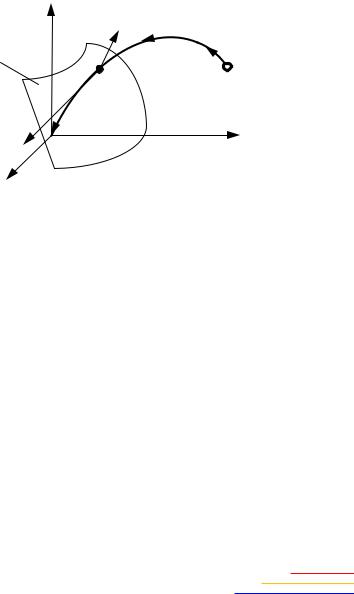
Очевидно, что совокупность частных производных функции Ляпунова составляет градиент функции V{x}, т.е. вектор, определяемый проекциями ∂V/∂xi на оси координат фазового пространства

Тогда в результате произведения градиента функции Ляпунова

V{x} и вектора фазовой скоростиf{x} = {f1; f2…fn} получается тоже некоторая скалярная функция координат состояния системы

Рис. 2.34. Граф ческое представление градиента функции Ляпунова

Если полная производная функции Ляпунова W{x} > 0, то, согласно формуле (2.170), вектор фазовой скорости f{x} составляет с вектором V{x} острый угол, фазовая траектория пересекает поверхность V{x} = const в сторону увеличения значений V{x}. Если же W{x} < 0, то угол между f{x} и V{x} тупой и фазовая траектория идет в сторону уменьшения значений V{x}. Уменьшение значений функции Ляпунова V{x} при пересечении её фазовой траекторией означает приближение последней к началу координат, в случае знакоопределенной V{x}, или к некоему стационарному состоянию, в сл учае знакопостоянной V{x}, т.е. стремление устойчивой системы к состоянию равновесия.

На основании вышеприведенных аналитических и графических заключений А.М. Ляпуновым были сформулированы следующие теоремы об устойчивости и неустойчивости нелинейных систем.

84

Теорема Ляпунова об устойчивости: если для системы, сво-

бодное движение которой описывается уравнениями (2.159), существует знакоопределенная функция V{x}, полная производная которой W{x} является знакопостоянной функцией противоположного знака, то система устойчива.

Теорема Ляпунова об асимптотической устойчивости: если для системы, свободное движение которой описывается уравнениями (2.159), существует знакоопределенная функция V{x}, полная производная которой W{x} является тоже знакоопределенной функцией противоположного знака, то система устойчива асимптотически.

Теорема Ляпунова о неустойчивости: если для системы, сво-

бодное движение которой описывается уравнениями (2.159), существует какая-нибудь функция V{x}, полная производная которой W{x} является тоже знакоопределенной функцией и в любой сколь угодно малой области вокруг начала координат имеет знак, совпадающий со знаком V{x}, то система неустойчива.

Рассмотрим пример исследования функции Ляпунова на знако-

Так как все положительны, то по критерию Сильвестра данная квадратичная форма является определенно-положительной функцией.

Рассмотрим пример определения устойчивости нелинейной АСУ, свободное движение которой задано системой дифференциальных уравнений состояния 1-го порядка в форме Коши:

85

где α, β, а, b – положительные постоянные числа; x1, x2 – фазовые координаты состояния системы.

Для анализа устойчивости системы выбираем положительноопределенную функцию Ляпунова в виде квадратичной формы

Рис. 2.35. Граница устойчивости системы

86