§ 2. Раскрытие неопределенностей по правилу Лопиталя
Ранее мы познакомились с примерами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞. Сейчас рассмотрим новое правило раскрытия этих неопределенностей.
Теорема
(правило Лопиталя).
Пусть функции f(x) и g(x) дифференцируемы
в некоторой окрестности точки a,
за исключением, быть может, самой точки a,
и пусть 
или
.
Тогда, если существует предел отношения
производных этих функций
,
то существует и предел отношения самих
функцийf(x)/g(x) при x→а, причем
|
|
(1) |
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Например,
найти 
.
Этот предел существует
.
Но отношение производных(1+cosx)/1=1+cos x при x→∞
не стремится ни к какому пределу.
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.
Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.
Примеры.
.
.
.
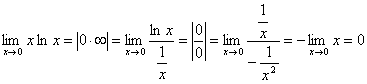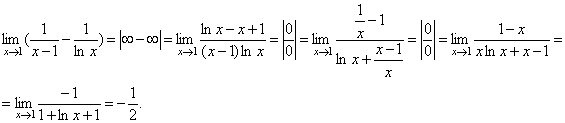
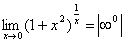
Обозначим 
.
Прологарифмируем
это равенство 
.
Найдем
.
Так
как lny функция
непрерывная, то 
.
Следовательно,
или
.
§ 3. Формула Тейлора
Пусть функция y= f(x) задана на (a, b) и x0 Î (a, b). Поставим следующую задачу: найти многочлен P(x), значения которого в окрестности точки x0 приближенно совпадали бы со значениями функции f(x) в соответствующих точках. Тогда можно будет считать, что f(x)≈P(x) и задачу вычисления значенийf(x) в окрестности точки x0 можно заменить более легкой задачей вычисления значений P(x).
Пусть искомый многочлен имеет степень n P(x) = Pn(x). Будем искать его в виде
|
|
(1) |
В
этом равенстве нам нужно найти
коэффициенты 
.
Для того чтобы этот многочлен был "близок" к функции f(x) потребуем выполнения следующих равенств:
Пусть
функция y=
f(x) имеет
производные до n-ого порядка. Найдем
коэффициенты 
многочленаPn(x)
исходя из условия равенства производных.
Введем обозначение n! = 1·2·3…n, 0! = 1, 1! = 1.
Подставим
в (1) x = x0 и
найдем 
,
но с другой стороны
.
Поэтому
Далее
найдем производную 
и
вычислим
Следовательно,
.
Учитывая третье условие и то, что
,
получим 
,
т.е.
.
Далее 
.
Значит,
,
т.е.
.
Очевидно,
что и для всех последующих коэффициентов
будет верна формула 
Подставляя
найденные значения коэффициентов 
в
формулу (1), получим искомый многочлен:
Обозначим 
и
назовем эту разностьn-ым
остаточным членом функции f(x) в
точке x0.
Отсюда 
и,
следовательно,
если
остаточный член будет мал.
Оказывается, что если x0 Î (a, b) при всех x Î (a, b) существует производная f (n+1)(x), то для произвольной точки x Î (a, b) существует точка, лежащая между x0 и x такая, что остаток можно представить в виде:
Это так называемая формула Лагранжа для остаточного члена.
Формула
где
x Î (x0, x)
называется формулой
Тейлора.
Если в этой формуле положить x0 = 0, то она запишется в виде
где x Î ( x0, x). Этот частный случай формулы Тейлора называют формулой МакЛорена.
Разложение в ряд Маклорена некоторых элементарных функций
Рассмотрим функцию f(x)=ex. Представим ее по формуле МакЛорена в виде суммы многочлена и некоторого остатка. Для этого найдем производные до (n+1) порядка:
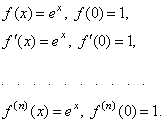
Таким образом, получаем
Используя эту формулу и придавая x различные значения, мы сможем вычислить значение ex.
Например, при x=1, ограничиваясь n=8, получим формулу, позволяющую найти приближенное значение числа e:
причем
остаток 
Отметим,
что для любого x Î R остаточный
член 
Действительно,
так как ξ Î (0; x),
то величина eξ ограничена
при фиксированном x.
При x>
0 eξ < ex.
Докажем, что при фиксированном x 
Имеем
Если x зафиксировано, то существует натуральное число N такое, что |x|<N.
Обозначим 
Заметив,
что 0<q<1, приn>N можем
написать
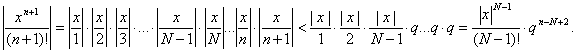
Но 
,
не зависящая отn,
а 
так
как q<1. Поэтому
Следовательно,
Таким образом, при любом x, взяв достаточное число слагаемых, мы можем вычислить ex с любой степенью точности.
Выпишем разложение по формуле МакЛорена для функции f(x)=sin x.
Найдем последовательные производные от функции f(x)=sin x.
Подставляя полученные значения в формулу МакЛорена, получим разложение:
Несложно заметить, что преобразовав n-й член ряда, получим
.
Так
как 
,
то аналогично разложениюex можно
показать, что 
для
всехx.
Пример. Применим полученную формулу для приближенного вычисления sin 20°. При n=3 будем иметь:
Оценим сделанную погрешность, которая равна остаточному члену:
Таким образом, sin 20°= 0,342 с точностью до 0,001.
f(x) = cos x. Аналогично предыдущему разложению можно вывести следующую формулу:
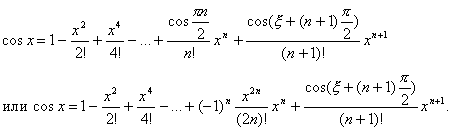
Здесь
также 
для
всехx. Докажите
формулу самостоятельно.
f(x)=ln (1+x). Заметим, что область определения этой функции D(y)=(–1; +∞).
Найдем формулу МакЛорена для данной функции.
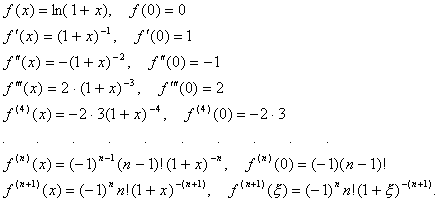
Подставим все найденные производные в ряд МакЛорена.
Можно
доказать, что если x Î (–1;1],то 
,
т.е. выведенная формула справедлива
приx Î (
–1;1].
f(x) = (1+x)m, где m Î R, m≠0.
При m≠Z данная функция определена при x> –1. Найдем формулу МакЛорена для этой функции:
И следовательно,
Можно
показать, что при |x|<1 