Министерство образования и науки

Российской Федерации

Федеральное агентство по образованию

Хакасский государственный университет

им. Н.Ф. Катанова

Е.В. Минакова

МАТЕМАТИКА

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Конспекты лекций для студентов,

обучающихся по направлению подготовки

230400.62 «Информационные системы и технологии»

Абакан

2011

Рецензенты:

Математика. Математический анализ: Конспект лекций по дисциплине «Математика. Математический анализ», предназначен для студентов, обучающихся по направлению подготовки 230400.62 «Информационные системы и технологии»

© Хакасский государственный

университет им. Н.Ф.Катанова, 2011

©Минакова Е.В.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Берман Г.Н. Сборник задач по курсу математического анализа. М., Наука, 1977.

2. Бохан К.А., Егорова И.А., Лащенов К.В. Курс математического анализа, т. 1. М., Просвещение, 1966.

3. Бохан К.А., Егорова И.А., Лащенов К.В. Курс математического анализа, т. 2. М., Просвещение, 1972.

4. Волковыский Л.И., Лунц Г.Л., Араманович И.Г. Сборник задач по теории функций комплексного переменного. М., Наука, 1970.

5. Вулих Б.З. Краткий курс теории функций вещественной переменной. М., Наука, 1975.

6. Вулих Б.З. Введение в функциональный анализ. М.:Наука, 1970.

7. Высшая математика / Под ред. Г. Н. Яковлева. – М.: Просвещение, 1988.

8. Данко П. Е., Попов А. Г., Кожевников Т. Я. Высшая математика в упражнениях и задачах. Т. 1-2. – М.: Просвещение, 1986.

9. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М., Наука, 1968.

10. Контарович, Акилов Функциональный анализ

11. Кудрявцев Л.Д. Математический анализ, тт. 1,2,3. М., Высшая школа, 1988.

12. Курош Высшая алгебра

13. Макаров И.П. Дополнительные главы математического анализа. М., Просвещение, 1968.

14. Маркушевич А.И. Краткий курс теории аналитических функций. М., Наука, 1966.

15. Маркушевич А.И., Маркушевич Л.А. Введение в теорию аналитических функций. М., Просвещение, 1977.

16. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. М., Высшая школа, 1967.

17. Очан Ю.С. Основы математического анализа. М., 1961.

18. Свешников А.Г., Тихонов А.Н.. Теория функций комплексной переменной. Учебник. М., 1999.

19. Уваренков И.М., Маллер М.З. Курс математического анализа, т. 1. М., Просвещение, 1966.

20. Уваренков И.М., Маллер М.З. Курс математического анализа, т. 2. М. Просвещение, 1976.

21. Фихтенгольц Г.М. Основы математического анализа, т. 1. М., Наука, 1968.

22. Фихтенгольц Г.М. Основы математического анализа, т. 2. М., Наука, 1968.

Раздел I. Введение в математический анализ

§ 1. Функция одной независимой переменной

Опр. 1.Рассмотрим два множестваХиУ, элементами которых могут быть любые объекты. Предложим, что каждому элементухмножестваХпо некоторому законуfили способу поставлен в соответствие определенный элементумножестваУ, тогда говорят что на множествеХзаданафункцияу = ƒ(х)(илиотображениемножестваХво множествоУ). МножествоХназываетсяобластью определенияфункции ƒ, а элементыу=ƒ(х)образуютмножество значенийфункции –У,х–независимая переменная(аргумент),у–зависимая переменная,ƒ–закон соответствия, знак функции.

Способы задания функции.Существует несколько способов задания функции:

а) аналитический способ, если функция задана формулой вида у= f(х);

б) табличный способ состоит в том, что функция задается таблицей, содержащей значения хи соответствующие значенияf(х);

в) графический способ, состоит в изображении графика функции – множество точек (х,у) плоскости, абсциссы которых есть значения аргументах, а ординаты – соответствующие им значения функцииу=f(х);

г) описательный способ, если функция записывается правилом ее составления.

Основные элементарные функции:

1. Степенная функция у=х^α;

2. Показательная функция у=а^х,а > 0,а ≠ 1;

3. Логарифмическая функция у=log_ах, а>0, а ≠ 1;

4. Тригонометрические функции: у=sinх, у=cosх , у=tgх, у=ctgх;

5. Обратные тригонометрические функции у=argsinх, у=arccosх, у=arctgх, у=arcctgх.

Опр. 2. Функции построенные из основных элементарных функций с помощью конечного числа алгебраических действий называютсяэлементарными.

Элементарные функции делятся на два класса.

1. Класс алгебраических функций:

а) целая алгебраическая функция (многочлен (полином) n-ой степени)у=А₀хⁿ+А₁х^n-1+А₂х^n-2+…+А_n-1х+А_n, гдеА₀, А₁, А₂, … , А_n– вещественные числа, коэффициенты многочлена;

б) у=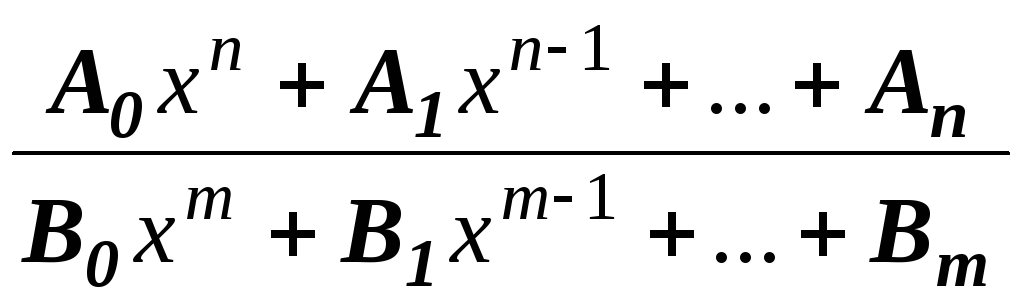дробно – рациональная функция, она представляет собой отношения двух многочленов;

в) иррациональная функция.

2. Класс трансцендентных функций:

а) показательная функция;

б) логарифмическая функция,

в) все тригонометрические функции,

г) все обратные тригонометрические функции,

д) функции вида у = х^α, где α – иррациональное число.

Обратная функция.

Опр. 3. Функцияу=f(х), определенная на промежуткеX, называетсяобратимойна промежуткеX, если любое свое значение она принимает только в одной точке этого промежутка; иными словами, если любым различным значениям аргумента соответствуют различные значения функции:

Сложная функция (суперпозиция функций). Пусть функцияу=f(u)есть функция от переменнойu, определенная на множествеUс областью значений –У, а переменнаяu=φ(х)функция от переменнойх, определенной на множествеХс областью значенияU. Тогда заданная на множествеХфункцияу=f(φ(x))называетсясложной функцией(функцией от функций).