§ 4. Промежутки возрастания и убывания функций

Вспомним сначала определения возрастающей и убывающей функций.

Функция y=f(x), определенная на некотором отрезке [a, b] (интервале (a, b)), называется возрастающей на этом отрезке, если большему значению аргумента x из [a, b] соответствует большее значение функции, то есть если x₁ < x₂, то f(x₁) < f(x₂).

Функцияy=f(x) называется убывающей на некотором отрезке [a, b], если меньшему значению аргумента x из [a, b]соответствует большее значение функции, то есть если x₁ <x₂, то f(x₁) > f(x₂).

Функция, только возрастающая или только убывающая на отрезке, называется монотонной на этом отрезке.

Функция y=f(x) называется постоянной на некотором отрезке [a, b], если при изменении аргумента x она принимает одни и те же значения.

Р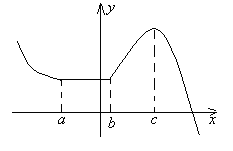ассмотрим график функции изображенной на рисунке и определим промежутки возрастания и убывания функции.

(-∞, a), (c, +∞) – убывает;

(a, b) – постоянная;

(b, c) – возрастает.

Применим понятие производной для исследования возрастания и убывания функции.

Теорема 1. (Необходимое и достаточное условия возрастания функции)

Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f '(x)≥ 0.

Обратно. Если функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b) и ее производная положительна на этом отрезке,f ' (x)≥ 0 для a<x<b, то f(x) возрастает на[a, b].

Доказательство.

Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) - f(x)>0. Но тогда и Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а 

Переходя в этом равенстве к пределу при Δx→0, получим , то естьf '(x)≥0.

Докажем вторую часть теоремы. Пусть f '(x)>0при всех x Î (a,b). Рассмотрим два любых значения x₁ и x₂ таких, что x₁ < x₂. Нужно доказать, что f(x₁)< f(x₂). По теореме Лагранжа существует такое число c Î (x₁, x₂), что . По условиюf '(x)>0, x₁ – x₂>0Þ , а это и значит, чтоf(x) – возрастающая функция.

Аналогичная теорема имеет место и для убывающих функций.

Теорема 2. Если f(x) убывает на[a,b], то на этом отрезке. Еслина (a; b), то f(x) убывает на [a, b],в предположении, чтоf(x) непрерывна на [a, b].

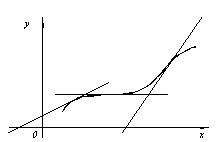
Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривойy=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tga≥0, а значит f '(x)≥0.

Аналогично иллюстрируется и вторая часть теоремы.

Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f '(x)>0 – для возрастания или f '(x)<0 – для убывания.

Примеры. Определить интервалы монотонности функции.

. Область определения заданной функции D(y) = (-∞; 0)È(0; +∞).

. Следовательно, f(x) – убывает на (-∞; 0) и (0; +∞).

 

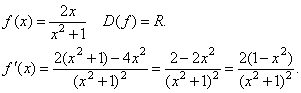
Найдем промежутки, на которых производная заданной функции положительна или отрицательна методом интервалов.

Итак, f(x) – убывает на (–∞; –1] и [1; +∞), возрастает на отрезке [–1; 1].

 

.

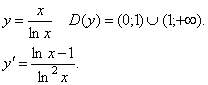Используя метод интервалов, получим f(x) убывает на (0; 1) и (1; e], возрастает на [e; +∞).