Раздел XI. Дифференциальные уравнения

§1. Задачи, приводящие к дифференциальным уравнениям. Определение и основные понятия

Опр. 1. Дифференциальными уравнениями называются уравнения, в которых неизвестными являются функции одной или нескольких переменных, и в уравнения входят не только сами функции, но и их производные. Если производные, входящие в уравнение, берутся только по одной переменной, то дифференциальное уравнение называется обыкновенным.

Опр. 2. Порядком дифференциального уравнения называется порядок высшей производной входящей в донное уравнение.

Опр. 3. Степенью дифференциального уравнения называется степень высшей в нем производной.

Опр. 4. Линейным дифференциальным уравнением первого порядка называется уравнение вида y’+p(x)y=f(x) (1) где p(x), f(x) – известные функции переменной х.

Опр. 5. Решением уравнения (1) называется такая функция y=φ(x), определенная на некотором промежутке (x₁,x₂), что при подстановке её вместо y в уравнение (1) получается верное равенство на всем промежутке (x₁,x₂).

Замечание. Очевидно, что подстановка y=φ(x) возможна только тогда, когда функция φ(x) на промежутке (x₁,x₂) имеет первую производную. Необходимо также, чтобы при любом значении переменной x из промежутка (x₁, x₂) точка с координатами x, y, y’ принадлежала множеству определения функций p(x) и f(x).

Опр. 6. Совокупность всех решений дифференциального уравнения называется его общим решением.

Опр. 7. Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных.

Опр. 8. График решения дифференциального уравнения называется интегральной кривой.

Теорема Коши. Если функция f(x,y) и ее частная производная f’_y(x,y) определены и непрерывны в некоторой области G плоскости Оху, то какова бы ни была внутренняя точка (х₀,у₀) области G, в некоторой окрестности этой точки существует единственное решение уравнения у’=f(x,y), удовлетворяющее условиям: у=у₀ при х=х₀ (2).

Опр. 9. Условия (2), в силу которых функция y=φ(x)принимает заданное значение у₀ в точке х₀, называют начальными условиями решения. Отыскание решения уравнения (1), удовлетворяющее начальным условиям (2) называется задачей Коши.

Рассмотрим несколько задач, приводящих к дифференциальным уравнениям.

Задача 1. На плоскости Оху найти кривую, проходящую через точку О(0,0), у которой угловой коэффициент касательной, проведенной к любой точке кривой, равен удвоенной абсциссе точки касания.

Задача 2. Найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t=0 и начальная скорость падения равна нулю.

Задача 3. Найти закон изменения числа живых организмов, обитающих в условиях неограниченных ресурсов питания (колония не подавляется никаким другим видом).

§ 2. Дифференциальные уравнения первого порядка

п. 1. Дифференциальные уравнения первого порядка с разделяющимися переменными

Опр. Если в уравнении y’=f(x,y) f(x,y)=f₁(x)f₂(y), то такое уравнение называется уравнением с разделяющимися переменными. Его общий вид:

Предполагая, что f₂(y)≠0, преобразуем последнее уравнение:

В обеих частях полученного уравнения стоят дифференциалы некоторых функций аргумента х. Из равенства дифференциалов этих функций следует, что сами функции отличаются одна от другой на константу.

Решение уравнения с разделяющимися переменными выполняется в следующем порядке:

1. Выполнить разделение переменных:

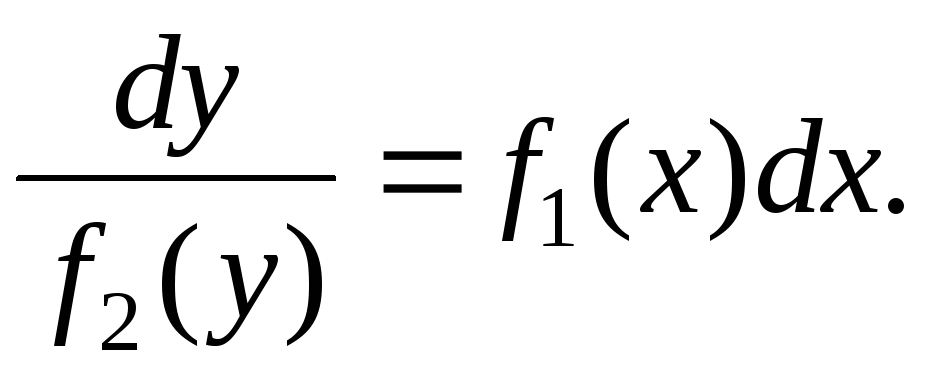
2. Проинтегрировать обе части уравнения:

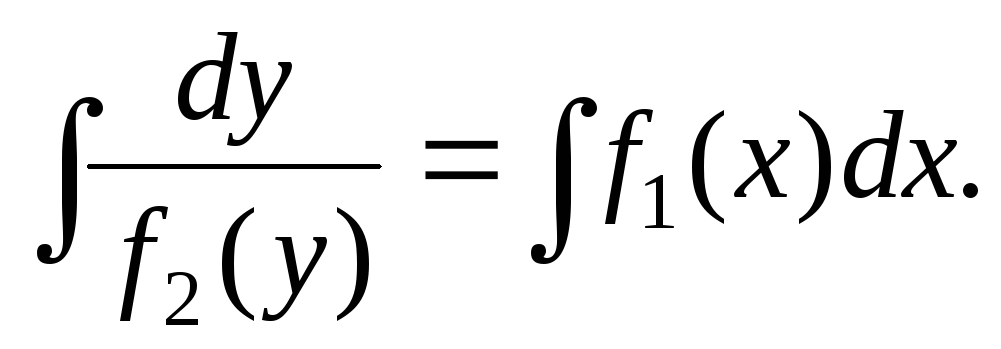
п. 2. Однородные дифференциальные уравнения первого порядка

Опр. 1. Уравнение вида f(x,y)dx=φ(x,y)dy, где f(x,y), φ(x,y) – однородные функции одной и той же степени, называется однородным.

Однородное уравнение посредством подстановки y=uv приводится к уравнению с разделяющимися переменными.

п. 3. Линейные дифференциальные уравнения первого порядка, уравнения Бернулли

Будем искать решение уравнения (1) в виде произведения y=uv (2) где u, v – неизвестные функции х. Находя производную y’=u’v+uv’ и подставляя значение у и у’ в уравнение (1), получим u’v+u(v’+p(x)v)=f(x) (3).

Выберем функцию v так, чтобы выражение в скобках равнялось нулю. Для этого надо решить уравнение с разделяющимися переменными v’+p(x)v=0.

Решая его, находим или(4).

Постоянную интегрирования в выражении (4) не пишем, поскольку нам достаточно найти только какую-нибудь одну функцию v, которая преобразовывает в ноль выражение в скобках в уравнении (3).

Подставляя (4) в (3), получим или(5). Подставляя (4) и (5) в (2), найдём общее решение уравнения (1):(6).

Опр. Уравнением Бернулли называется уравнение вида y’+p(x)y=q(x)y^α,

где p(x), q(x) – известные функции х, α≠0, α≠1.

Замечание. На практике помнить формулу (6) не обязательно: достаточно лишь помнить, что линейные дифференциальные уравнения первого порядка, а также уравнения Бернулли, решаются методом Бернулли с помощью подстановки y=uv.