§ 4. Функциональные ряды

Опр. 1. Ряд , членами которого являются функции отх, называется функциональным рядом.

Давая переменной х конкретные числовые значения, получим разные числовые ряды, которые могут быть сходящимися или расходящимися.

Опр. 2. Множество всех значений х, для которых ряд сходящийся, называетсяобластью сходимости этого ряда.

Опр. 3. Функциональный ряд вида (1) гдех₀, а₀ – числа, называется степенным рядом.

Переобозначив х-х₀ на х, ряд (1) всегда можно свести к виду (2).

Для простоты будем изучать ряды вида (2). Ряд (2) всегда сходится, по крайней мере, в точке х=0.

Теорема Абеля. Если ряд (2) сходящийся при х=х₀≠0, то он абсолютно сходящийся для всех значений х, что удовлетворяют неравенству , то есть в интервале. Если прих=х₁ ряд (2) расходящийся, то он расходящийся для всех значений х, что удовлетворяют неравенству .

Из теоремы Абеля следует, что если ряд (2) сходится хотя бы в одной точке х=х₀≠0, то существует такое число R>0, что при ряд сходится абсолютно, а прирасходится. Это числоR называют радиусом сходимости степенного ряда, а интервал (-R,R) – его интервалом сходимости.

Радиус сходимости ряда (2) можно найти по формулам

или . (3)

Вывод. Чтобы найти область сходимости ряда (2) надо:

1. найти интервал сходимости (-R,R) ряда, применяя к ряду признаки Даламбера и Коши, или пользуясь формулами (3);

2. исследовать сходимость ряда на концах интервала сходимости, то есть в точках x=±R.

§ 5. Ряд Маклорена

В середине интервала сходимости степенные ряды можно почленно интегрировать и дифференцировать, причём полученные при этом ряды будут иметь тот же радиус сходимости, что и исходный ряд.

Необходимое и достаточное условия разложимости функции в степенной ряд. Если функция f(х) в интервале (x₀ - R,x₀+R) имеет производные всех порядков и существует такое число М>0, что,,п=0, 1, 2,…, где , то функциюf(х) можно разложить в ряд Тейлора:

При ряд Тейлора имеет вид

и называется рядом Маклорена.

Формально ряд Тейлора можно написать для всякой функции, которая в окрестности точки x₀ имеет производные любого порядка. Однако этот ряд будет сходиться к породившей его функции f (x) только при тех значениях x, при которых остаточный член R_n(x) при неограниченном возрастании n стремится к нулю.

Для разложения данной функции в ряд Тейлора нужно:

1) написать ряд Тейлора для данной функции, т. е. вычислить значения этой функции и её производных при x=х₀ и подставить их в общее выражение ряда Тейлора;

2) исследовать остаточный R_n член формулы Тейлора для данной функции и определить те значения x, при которых полученный ряд сходится к данной функции, т. е. при которых

§ 5. Методы разложения функций в ряд Тейлора

1. Метод, использующий формулу бесконечно убывающей геометрической прогрессии:

Пример. Разложить функцию в ряд Тейлора.

Решение. Представим функцию f(x) в виде суммы простых дробей, используя метод неопределенных коэффициентов:

2. Метод подстановки

Пример. Разложить функцию в ряд Тейлора.

Решение. Обозначим . Тогдаи

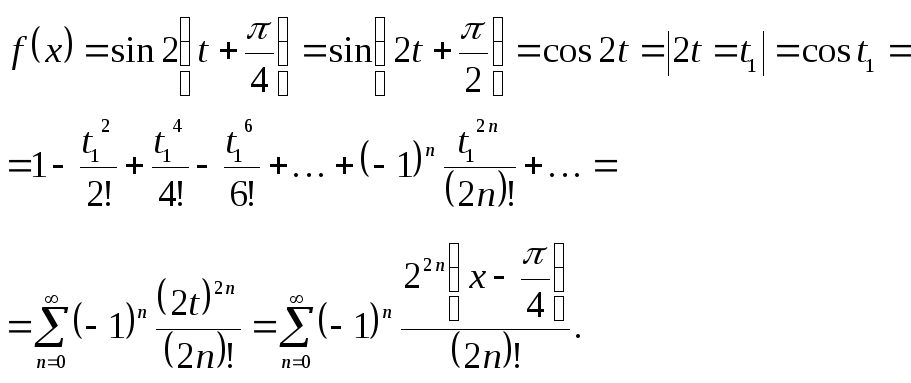
3. Метод интегрирования

Пример. Разложить в ряд Маклорена функцию

Решение. Проинтегрируем функцию

4. Метод диференцирования

Пример. Разложить функцию в ряд Тейлора.

Решение. Продифференцируем функцию . Тогда

Приведём примеры рядов Маклорена некоторых элементарных функций:

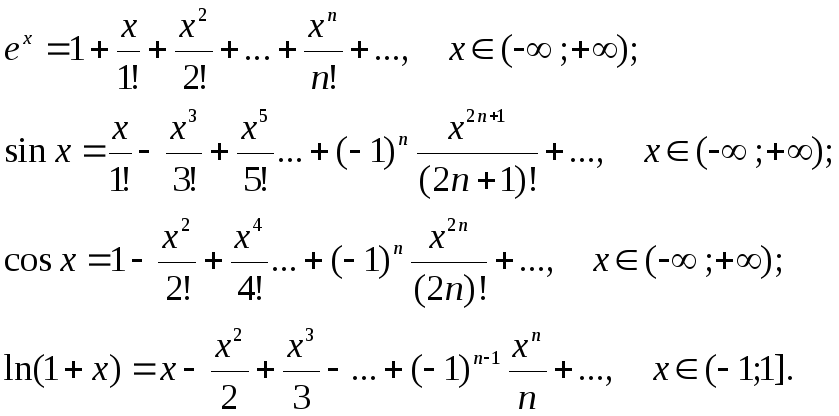
§ 6. Применение степенных рядов при приближенных вычислениях значения функции

Ряды широко используются для приближённого вычисления функций, интегралов, для приближённого интегрирования дифференциальных уравнений.

Пусть надо найти f(x₀) для функции f(x), которая раскладывается в степенной ряд

Тогда Заменяя значениеf(x₀) суммой n членов этого ряда получаем приближенное значениеf(x₀), при этом ошибка равна В силу сходимости ряда (1) в точкех=х₀, при достаточно большом n эта ошибка станет сколь угодно малой и S_n дает значение f(x₀) с любой наперед заданной точностью. Для вычисления f(x₀) с заданной точностью надо уметь производить оценку остатка (2), что позволяет брать требуемое число членов в S_n.

Оценка остатка ряда особенно проста, если ряд удовлетворяет признаку Лейбница. В этом случае остаток имеет знак своего первого члена и по абсолютной величине меньше его.

В случае произвольного ряда абсолютная величина R_n не превосходит суммы абсолютных величин членов, входящих в R_n. Для уже полученного положительного ряда стараются найти легко суммируемый ряд из положительных членов, члены которого были бы меньше абсолютных величин членов остатка, и оценивают остаток суммой этого ряда.