
- •Министерство образования и науки
- •Раздел I. Введение в математический анализ
- •§ 1. Функция одной независимой переменной
- •§ 2. Основные свойства функций
- •§ 3. Числовая последовательность. Предел числовой последовательности
- •§ 4. Предел функции
- •§ 5. Бесконечно большие и бесконечно малые функции
- •§ 6. Замечательные пределы
- •§ 7. Эквивалентные функции
- •§ 8. Односторонние пределы
- •§ 9. Непрерывность функции
- •§ 10. Точки разрыва функции
- •Раздел IV. Производная и дифференциал
- •§ 1. Производная функции одной независимой переменной
- •§ 2. Правила дифференцирования функций
- •§ 3. Дифференциал. Геометрический смысл дифференциала
- •§ 3. Производные и дифференциалы высших порядков
- •§ 4. Применение дифференциала к приближенным вычислениям
- •Раздел V. Приложения производной
- •§ 1. Теоремы Ролля, Лагранжа, Коши
- •§ 2. Раскрытие неопределенностей по правилу Лопиталя
- •§ 3. Формула Тейлора
- •§ 4. Промежутки возрастания и убывания функций
- •§ 5. Экстремумы функций
- •§ 6. Наибольшее и наименьшее значения функции на отрезке
- •§ 7. Выпуклость и вогнутость функции. Точки перегиба
- •§ 8. Асимптоты
- •§ 9. Общий план исследования функций и построение графиков
- •Раздел VI. Комплексные числа
- •§ 1. Основные понятия
- •§ 2. Операции над комплексными числами в алгебраической форме
- •§ 3. Связь комплексных и действительных чисел. Геометрическая интерпретация комплексных чисел, модуль и аргумент комплексного числа, главное значение аргумента
- •§ 4. Тригонометрическая и показательная формы записи комплексного числа
- •§ 5. Решение квадратных уравнений, не имеющих действительных корней
- •Раздел VII. Неопределенный интеграл
- •§1. Первообразная. Неопределенный интеграл и его свойства
- •§ 2. Таблица основных интегралов
- •§ 3. Методы интегрирования
- •§ 4. Интегрирование рациональных дробей
- •§ 5. Интегрирование некоторых иррациональных и тригонометрических функций
- •Раздел VIII. Определённый интеграл
- •§ 1. Определенный интеграл. Геометрический смысл определённого интеграла.
- •Свойства определённого интеграла.
- •§ 2. Формула Ньютона-Лейбница.
- •§ 2. Интегрирование по частям и замена переменной в определенном интеграле
- •§ 3. Несобственные интегралы
- •Раздел IX. Дифференциальное исчисление функций нескольких переменных.
- •§ 1. Определение функции двух и более переменных
- •§ 2. Предел функции в точке. Непрерывность функции в точке и на множестве
- •§ 3. Частные производные. Полный дифференциал
- •§ 4. Производная по направлению и градиент функции двух переменных
- •§ 5. Экстремумы функций нескольких переменных.
- •Раздел X. Интегральное исчисление функций нескольких переменных.
- •§ 1. Двойной интеграл
- •§ 2. Криволинейные интегралы
- •Раздел XI. Дифференциальные уравнения
- •§1. Задачи, приводящие к дифференциальным уравнениям. Определение и основные понятия
- •§ 2. Дифференциальные уравнения первого порядка
- •§3. Дифференциальные уравнения 2-го порядка
- •Раздел XII. Ряды
- •§ 1.Числовые ряды: основные понятия
- •§ 2. Признаки сходимости числовых рядов
- •§ 3. Знакочередующиеся ряды
- •§ 4. Функциональные ряды
- •§ 5. Ряд Маклорена
- •§ 5. Методы разложения функций в ряд Тейлора
- •§ 7. Ряды Фурье
- •Раздел XIII. Теория функции комплексного переменного
- •§ 1. Функции комплексного переменного
- •§ 2. Дифференцируемость функции комплексной переменной.
Свойства определённого интеграла.
Линейность. Если функции y = f(x), y = g(x) интегрируемы по отрезку [a,b] , то по этому отрезку интегрируема их линейная комбинация A f(x) + B g(x) (A, B = const), и

 .
.Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то

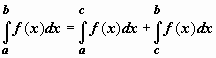 .
.Интеграл от единичной функции ( f(x) = 1). Если f(x) = 1, то
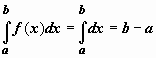 .
.
§ 2. Формула Ньютона-Лейбница.
Значение
определённого интеграла не зависит от
того, какой буквой обозначена переменная
интегрирования:  (чтобы
убедиться в этом, достаточно выписать
интегральные суммы, они совпадают). В
этом разделе переменную интегрирования
будем обозначать буквойt,
а буквой x обозначим
верхний предел интегрирования. Будем
считать, что верхний предел интеграла
может меняться, т.е. что x -
переменная, в результате интеграл будет
функцией Ф(x) своего
верхнего предела:
(чтобы
убедиться в этом, достаточно выписать
интегральные суммы, они совпадают). В
этом разделе переменную интегрирования
будем обозначать буквойt,
а буквой x обозначим
верхний предел интегрирования. Будем
считать, что верхний предел интеграла
может меняться, т.е. что x -
переменная, в результате интеграл будет
функцией Ф(x) своего
верхнего предела:  .
Легко доказать, что еслиf(t) интегрируема,
то Ф(x) непрерывна,
но для нас важнее следующая фундаментальная
теорема:
.
Легко доказать, что еслиf(t) интегрируема,
то Ф(x) непрерывна,
но для нас важнее следующая фундаментальная
теорема:
![]() Теорема
об интеграле с переменным верхним
пределом.
Если функция f(t) непрерывна
в окрестности точки t = x,
то в этой точке функция Ф(x) дифференцируема,
и
Теорема
об интеграле с переменным верхним
пределом.
Если функция f(t) непрерывна
в окрестности точки t = x,
то в этой точке функция Ф(x) дифференцируема,
и ![]() .
.![]() Другими
словами, производная определённого
интеграла от непрерывной функции по
верхнему пределу равна значению
подынтегральной функции в этом
пределе.
Другими
словами, производная определённого
интеграла от непрерывной функции по
верхнему пределу равна значению
подынтегральной функции в этом
пределе.
![]() Док-во.
Дадим верхнему пределу x приращение
Док-во.
Дадим верхнему пределу x приращение ![]() .
Тогда
.
Тогда
 ,
гдеc -
точка, лежащая между x и
,
гдеc -
точка, лежащая между x и ![]() (существование
такой точки утверждается теоремой о
среднем; цифры над знаком равенства -
номер применённого свойства определённого
интеграла).
(существование
такой точки утверждается теоремой о
среднем; цифры над знаком равенства -
номер применённого свойства определённого
интеграла).![]() .
Устремим
.
Устремим![]() .
При этом
.
При этом![]() (c-
точка, расположенная междуx и
(c-
точка, расположенная междуx и ![]() ).
Так какf(t) непрерывна
в точке t = x,
то
).
Так какf(t) непрерывна
в точке t = x,
то ![]() .
Следовательно, существует
.
Следовательно, существует![]() ,
и
,
и![]() .
Теорема доказана.
.
Теорема доказана.
![]() Отметим
первое важное следствие этой теоремы.
По существу, мы доказали, что любая
непрерывная функция f(x) имеет
первообразную, и эта первообразная
определяется формулой
Отметим
первое важное следствие этой теоремы.
По существу, мы доказали, что любая
непрерывная функция f(x) имеет
первообразную, и эта первообразная
определяется формулой 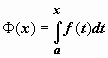 .
Другим важным следствием этой теоремы
является формула Ньютона-Лейбница, или
основная формула интегрального
исчисления.
.
Другим важным следствием этой теоремы
является формула Ньютона-Лейбница, или
основная формула интегрального
исчисления.
Формула
Ньютона-Лейбница. Если f(x) непрерывна
на отрезке [a, b],
и F(x) -
некоторая первообразная функции ![]() ,
то
,
то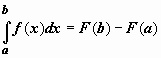 .Док-во. Мы
установили, что функция
.Док-во. Мы
установили, что функция 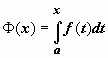 -
первообразная непрерывнойf(x).
Так как F(x) -
тоже первообразная, то Ф(x)
= F(x)
+ C. Положим
в этом равенстве x =a.
Так как
-
первообразная непрерывнойf(x).
Так как F(x) -
тоже первообразная, то Ф(x)
= F(x)
+ C. Положим
в этом равенстве x =a.
Так как  ,
то
,
то .
В равенстве
.
В равенстве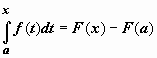 переобозначим
переменные: для переменной
интегрированияt вернёмся
к обозначению x ,
верхний предел x обозначим b.
Окончательно,
переобозначим
переменные: для переменной
интегрированияt вернёмся
к обозначению x ,
верхний предел x обозначим b.
Окончательно, 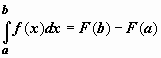 .
.![]() Разность
в правой части формулы Ньютона-Лейбница
обозначается специальным
символом:
Разность
в правой части формулы Ньютона-Лейбница
обозначается специальным
символом:![]() (здесь
(здесь![]() читается
как "подстановка отa до b"),
поэтому формулу Ньютона-Лейбница обычно
записывают так:
читается
как "подстановка отa до b"),
поэтому формулу Ньютона-Лейбница обычно
записывают так: 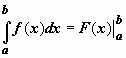 .
.![]() Пример
применения формулы Ньютона-Лейбница:
Пример
применения формулы Ньютона-Лейбница: .
.
§ 2. Интегрирование по частям и замена переменной в определенном интеграле
Формула интегрирования по частям для определённого интеграла.
Если u(x), v(x) -
непрерывно дифференцируемые функции,
то 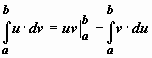 .
.![]() Док-во.
Интегрируем равенство
Док-во.
Интегрируем равенство ![]() в
пределах отa до b:
в
пределах отa до b: 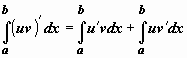 .
Функция в левом интеграле имеет
первообразнуюuv,
по формуле Ньютона-Лейбница
.
Функция в левом интеграле имеет
первообразнуюuv,
по формуле Ньютона-Лейбница 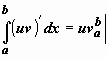 ,
следовательно,
,
следовательно, ,
откуда и следует доказываемое
равенство.
,
откуда и следует доказываемое
равенство.![]() Пример:
Пример: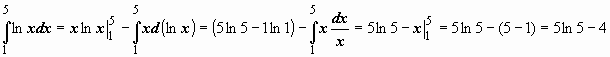 .
.
Замена переменной в определённом интеграле.
Теорема.
Пусть функция ![]()
определена, непрерывно дифференцируема и монотонна на отрезке
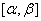 ,
,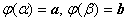 ,
,функция
 непрерывна
на отрезке [a, b].
непрерывна
на отрезке [a, b].
Тогда 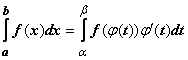 .
.
Док-во.
Пусть F(x) -
первообразная для функции f(x),
т.е. ![]() ,
тогда
,
тогда![]() -
первообразная для функции
-
первообразная для функции![]() .
.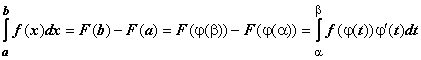 ,
что и требовалось доказать.
,
что и требовалось доказать.
![]() При
решении задач нельзя забывать о том,
что при переходе к новой переменной
надо обязательно вычислить новые пределы
интеграла.
При
решении задач нельзя забывать о том,
что при переходе к новой переменной
надо обязательно вычислить новые пределы
интеграла.
![]() Пример:
Пример:

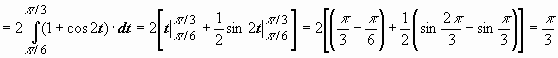 .
.
