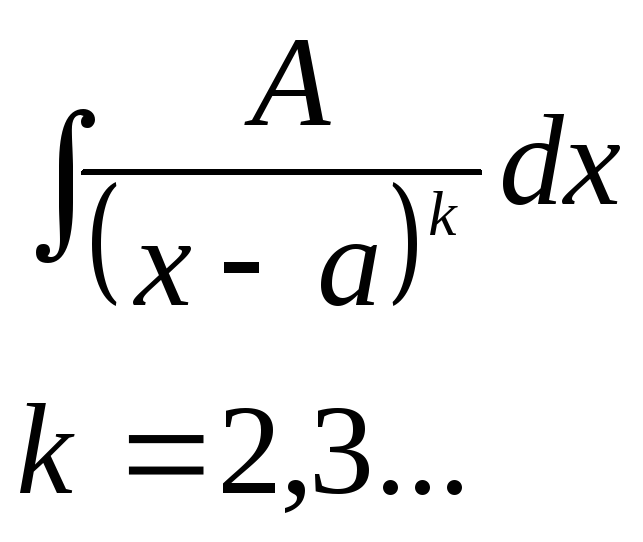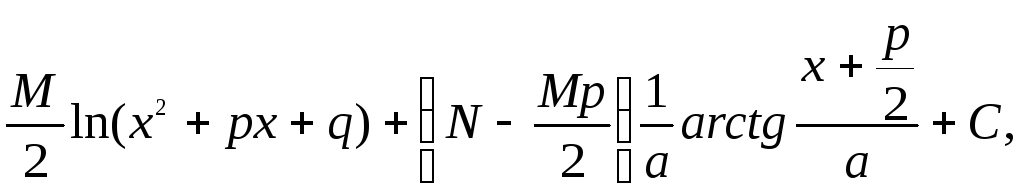- •Министерство образования и науки
- •Раздел I. Введение в математический анализ
- •§ 1. Функция одной независимой переменной
- •§ 2. Основные свойства функций
- •§ 3. Числовая последовательность. Предел числовой последовательности
- •§ 4. Предел функции
- •§ 5. Бесконечно большие и бесконечно малые функции
- •§ 6. Замечательные пределы
- •§ 7. Эквивалентные функции
- •§ 8. Односторонние пределы
- •§ 9. Непрерывность функции
- •§ 10. Точки разрыва функции
- •Раздел IV. Производная и дифференциал
- •§ 1. Производная функции одной независимой переменной
- •§ 2. Правила дифференцирования функций
- •§ 3. Дифференциал. Геометрический смысл дифференциала
- •§ 3. Производные и дифференциалы высших порядков
- •§ 4. Применение дифференциала к приближенным вычислениям
- •Раздел V. Приложения производной
- •§ 1. Теоремы Ролля, Лагранжа, Коши
- •§ 2. Раскрытие неопределенностей по правилу Лопиталя
- •§ 3. Формула Тейлора
- •§ 4. Промежутки возрастания и убывания функций
- •§ 5. Экстремумы функций
- •§ 6. Наибольшее и наименьшее значения функции на отрезке
- •§ 7. Выпуклость и вогнутость функции. Точки перегиба
- •§ 8. Асимптоты
- •§ 9. Общий план исследования функций и построение графиков
- •Раздел VI. Комплексные числа
- •§ 1. Основные понятия
- •§ 2. Операции над комплексными числами в алгебраической форме
- •§ 3. Связь комплексных и действительных чисел. Геометрическая интерпретация комплексных чисел, модуль и аргумент комплексного числа, главное значение аргумента
- •§ 4. Тригонометрическая и показательная формы записи комплексного числа
- •§ 5. Решение квадратных уравнений, не имеющих действительных корней
- •Раздел VII. Неопределенный интеграл
- •§1. Первообразная. Неопределенный интеграл и его свойства
- •§ 2. Таблица основных интегралов
- •§ 3. Методы интегрирования
- •§ 4. Интегрирование рациональных дробей
- •§ 5. Интегрирование некоторых иррациональных и тригонометрических функций
- •Раздел VIII. Определённый интеграл
- •§ 1. Определенный интеграл. Геометрический смысл определённого интеграла.
- •Свойства определённого интеграла.
- •§ 2. Формула Ньютона-Лейбница.
- •§ 2. Интегрирование по частям и замена переменной в определенном интеграле
- •§ 3. Несобственные интегралы
- •Раздел IX. Дифференциальное исчисление функций нескольких переменных.
- •§ 1. Определение функции двух и более переменных
- •§ 2. Предел функции в точке. Непрерывность функции в точке и на множестве
- •§ 3. Частные производные. Полный дифференциал
- •§ 4. Производная по направлению и градиент функции двух переменных
- •§ 5. Экстремумы функций нескольких переменных.
- •Раздел X. Интегральное исчисление функций нескольких переменных.
- •§ 1. Двойной интеграл
- •§ 2. Криволинейные интегралы
- •Раздел XI. Дифференциальные уравнения
- •§1. Задачи, приводящие к дифференциальным уравнениям. Определение и основные понятия
- •§ 2. Дифференциальные уравнения первого порядка
- •§3. Дифференциальные уравнения 2-го порядка
- •Раздел XII. Ряды
- •§ 1.Числовые ряды: основные понятия
- •§ 2. Признаки сходимости числовых рядов
- •§ 3. Знакочередующиеся ряды
- •§ 4. Функциональные ряды
- •§ 5. Ряд Маклорена
- •§ 5. Методы разложения функций в ряд Тейлора
- •§ 7. Ряды Фурье
- •Раздел XIII. Теория функции комплексного переменного
- •§ 1. Функции комплексного переменного
- •§ 2. Дифференцируемость функции комплексной переменной.
§ 4. Интегрирование рациональных дробей
п. 1. Интегрирование простейших рациональных функций (простых дробей)
|
Интеграл |
Результат интегрирования |
|
|
|
|
|
|
|
|
где
|
где А, М, N, а, р, q – действительные числа, x2+px+q, не имеет действительных корней.
п. 2. Интегрирование правильных дробей
Опр.
Рациональная
дробь
![]() называетсяправильной,
если степень многочлена
называетсяправильной,
если степень многочлена
![]() меньше степени многочлена
меньше степени многочлена![]()
Интегрирование правильных дробей основано на следующей теореме.
Теорема. Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа простых дробей.
Используется следующая формула:
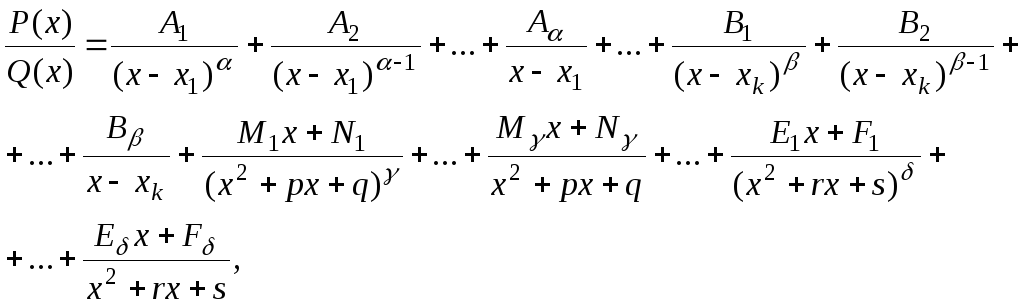 *
*
где
![]()
![]() действительные
корни многочлена
действительные
корни многочлена![]() кратности
кратности![]() а квадратные трехчлены не имеют
действительных корней).
а квадратные трехчлены не имеют
действительных корней).
Для того чтобы найти неизвестные коэффициенты, надо:
дроби в правой части привести к общему знаменателю, которым, очевидно, будет
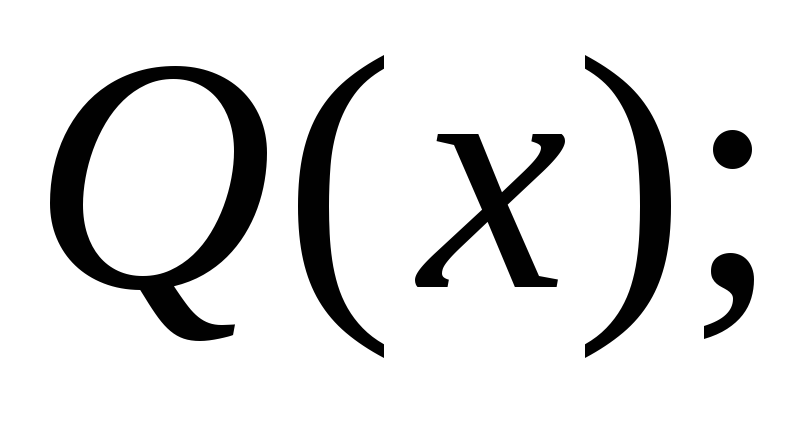
приравнять числители левой и правой частей. В результате получится равенство двух многочленов;
из равенства найти неизвестные коэффициенты;
подставив найденные коэффициенты в формулу (*) получим разложение правильной дроби на сумму простых дробей.
Т.о., интегрирование правильной дроби сводится к интегрированию простых дробей.
п. 3. Интегрирование рациональных функций
Пусть нам дана рациональная функция. Если она представляет собой правильную дробь, то интегрировать ее мы уже умеем. Если дробь неправильная, то выделив из нее целую часть (разделив числитель на знаменатель), сведем вычисление интеграла к вычислению правильной дроби.
§ 5. Интегрирование некоторых иррациональных и тригонометрических функций
п. 1. Интегрирование некоторых тригонометрических функций
При
вычислении интегралов вида
![]() или
или![]() приn
четном нужно представить его в виде
приn
четном нужно представить его в виде
![]() раскрыть скобки и, если потребуется,
повторно применить формулу
раскрыть скобки и, если потребуется,
повторно применить формулу![]()
При
вычислении интегралов вида
![]()
![]()
![]() применяются формулы:
применяются формулы:

При
вычислении интегралов вида
![]() и
и![]() (n
– целое положительное число) для первого
интеграла за вспомогательную функцию
нужно принять
(n
– целое положительное число) для первого
интеграла за вспомогательную функцию
нужно принять
![]() и для второго
и для второго![]()
п. 2. Интегрирование некоторых иррациональных функций
При
вычислении некоторых интегралов аргумент
х
необходимо заменить функцией новой
переменной u:
![]() К таким подстановкам относятся
тригонометрические подстановки:
К таким подстановкам относятся
тригонометрические подстановки:
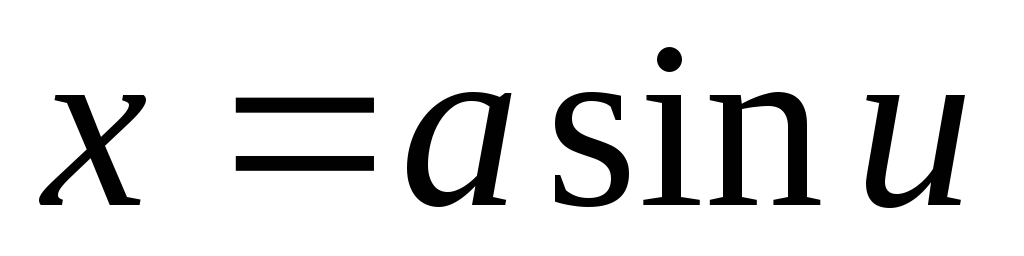 в
интегралах, содержащих
в
интегралах, содержащих
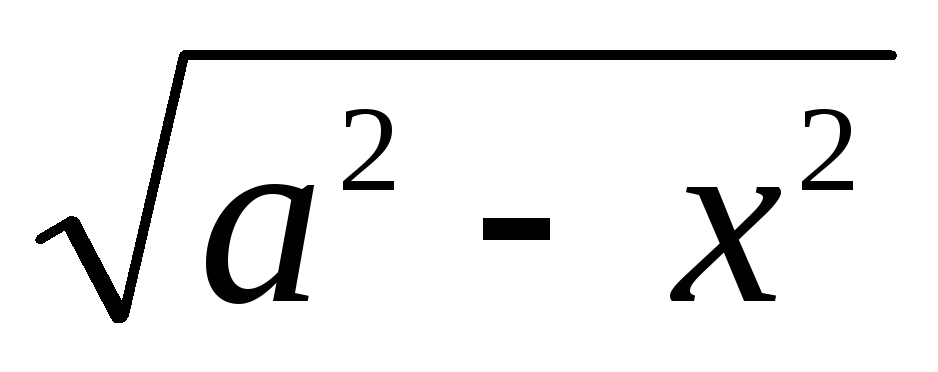 ;
;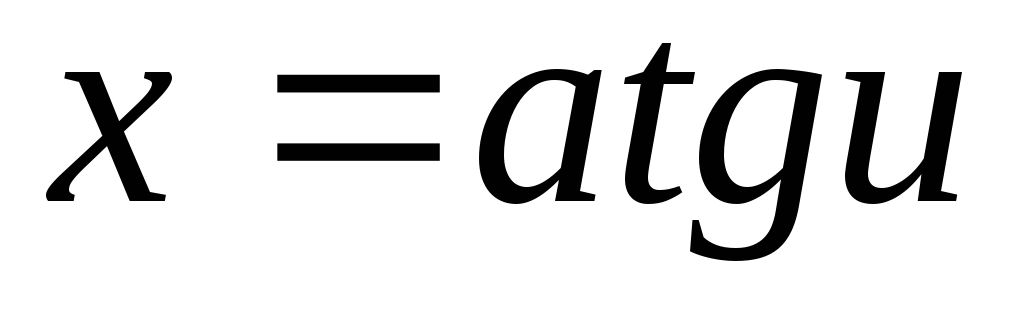 в
интегралах, содержащих
в
интегралах, содержащих
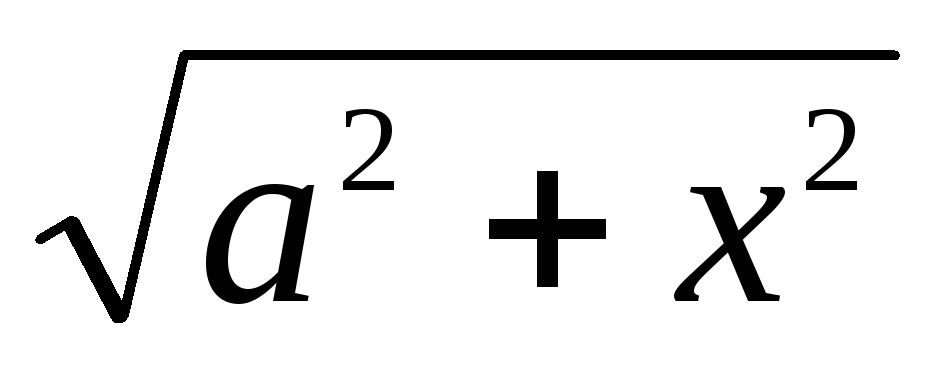 ;
;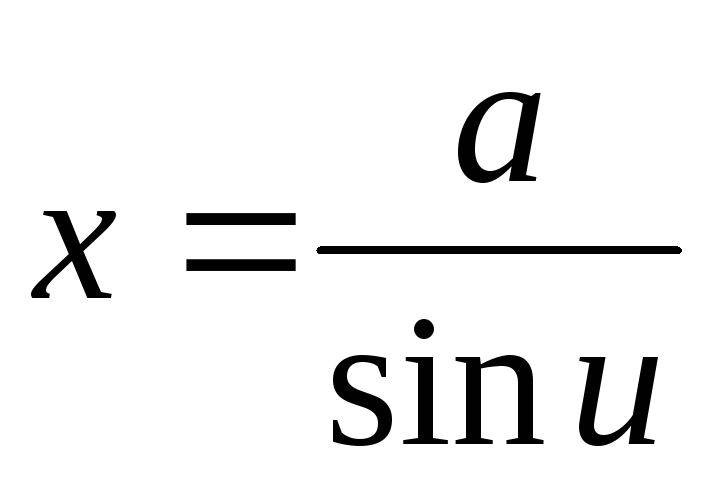 или
или
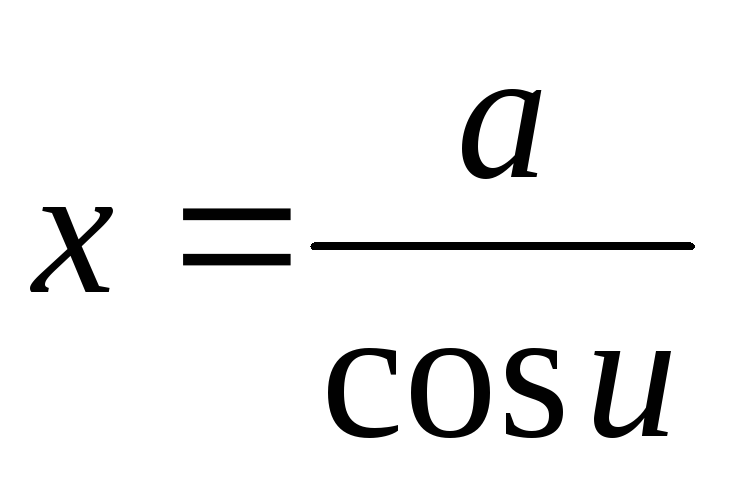 в интегралах, содержащих
в интегралах, содержащих .
.
Раздел VIII. Определённый интеграл
§ 1. Определенный интеграл. Геометрический смысл определённого интеграла.
Пусть
на отрезке [a,b]
(b>a) задана
непрерывная функция y = f(x) ,
принимающая на этом отрезке неотрицательные
значения : ![]() при
при![]() .
Требуется определить площадьS криволинейной
трапеции ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x = a и x = b,
сверху – функцией y = f(x).
.
Требуется определить площадьS криволинейной
трапеции ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x = a и x = b,
сверху – функцией y = f(x). 
![]() Для
решения этой задачи разделим произвольным
образом основаниеAD фигуры
точками x0 = a, x1 , x2 ,
…, xn-1
= a, xn = b на n частей [x0 , x1],
[x1 , x2],
…, [xi-1
, xi],
…, [xn-1
,xn]; символом
Для
решения этой задачи разделим произвольным
образом основаниеAD фигуры
точками x0 = a, x1 , x2 ,
…, xn-1
= a, xn = b на n частей [x0 , x1],
[x1 , x2],
…, [xi-1
, xi],
…, [xn-1
,xn]; символом ![]() будем
обозначать длинуi-го
отрезка:
будем
обозначать длинуi-го
отрезка: ![]() .
На каждом из отрезков [xi-1
, xi] выберем
произвольную точку
.
На каждом из отрезков [xi-1
, xi] выберем
произвольную точку ![]() ,
найдём
,
найдём![]() ,
вычислим произведение
,
вычислим произведение![]() (это
произведение равно площади
прямоугольникаPi с
основанием [xi-1
, xi] и
высотой
(это
произведение равно площади
прямоугольникаPi с
основанием [xi-1
, xi] и
высотой ![]() )
и просуммируем эти произведения по всем
прямоугольникам. Полученную сумму
обозначимS ступ:
)
и просуммируем эти произведения по всем
прямоугольникам. Полученную сумму
обозначимS ступ:  .
.![]() Sступ равно
площади ступенчатой фигуры, образованной
прямоугольниками Pi , i =
1,2,…,n; на
левом рисунке эта площадь
заштрихована. Sступ не
равна искомой площади S,
она только даёт некоторое приближение
к S.
Для того, чтобы улучшить это приближение,
будем увеличивать количество n отрезков
таким образом, чтобы максимальная длина
этих отрезков
Sступ равно
площади ступенчатой фигуры, образованной
прямоугольниками Pi , i =
1,2,…,n; на
левом рисунке эта площадь
заштрихована. Sступ не
равна искомой площади S,
она только даёт некоторое приближение
к S.
Для того, чтобы улучшить это приближение,
будем увеличивать количество n отрезков
таким образом, чтобы максимальная длина
этих отрезков ![]() стремилась
к нулю (на рисунке ступенчатые фигуры
изображены приn =
7 (слева) и при n =
14 (справа)). При
стремилась
к нулю (на рисунке ступенчатые фигуры
изображены приn =
7 (слева) и при n =
14 (справа)). При ![]() разница
междуSступ иS будет
тоже стремиться к нулю, т.е.
разница
междуSступ иS будет
тоже стремиться к нулю, т.е.
![]()
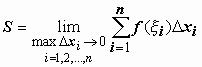 .
.
Определение
определённого интеграла.
Пусть на отрезке [a,b] задана
функция y = f(x).
Разобьём отрезок [a,b] произвольным
образом на n частей
точками [x0 , x1],
[x1 ,x2],
…, [xi-1
, xi],
…, [xn-1
, xn]; длину i-го
отрезка обозначим ![]() :
:![]() ;
максимальную из длин отрезков обозначим
;
максимальную из длин отрезков обозначим![]() .
На каждом из отрезков[xi-1
, xi] выберем
произвольную точку
.
На каждом из отрезков[xi-1
, xi] выберем
произвольную точку ![]() и
составим сумму
и
составим сумму .
.![]() Сумма
Сумма![]() называется
интегральной суммой. Если существует
(конечный) предел последовательности
интегральных сумм
называется
интегральной суммой. Если существует
(конечный) предел последовательности
интегральных сумм![]() при
при![]() ,
не зависящий ни от способа разбиения
отрезка [a,b] на
части [xi-1
, xi],
ни от выбора точек
,
не зависящий ни от способа разбиения
отрезка [a,b] на
части [xi-1
, xi],
ни от выбора точек ![]() ,
то функцияf(x) называется
интегрируемой по отрезку [a,b],
а этот предел называется определённым
интегралом от функцииf(x) по
отрезку [a,b] и
обозначается
,
то функцияf(x) называется
интегрируемой по отрезку [a,b],
а этот предел называется определённым
интегралом от функцииf(x) по
отрезку [a,b] и
обозначается 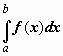 .
.![]() Функцияf(x),
как и в случае неопределённого интеграла,
называется подынтегральной, числа a и b -
соответственно, нижним и верхним
пределами интегрирования.
Функцияf(x),
как и в случае неопределённого интеграла,
называется подынтегральной, числа a и b -
соответственно, нижним и верхним
пределами интегрирования.
![]() Кратко
определение иногда записывают так:
Кратко
определение иногда записывают так:![]()
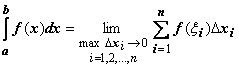 .
.![]() В
этом определении предполагается,
чтоb> a.
Для других случаев примем, тоже по
определению:
Если b=a,
то
В
этом определении предполагается,
чтоb> a.
Для других случаев примем, тоже по
определению:
Если b=a,
то  ;
еслиb<a,
то
;
еслиb<a,
то  .
.
![]() Теорема
существования определённого интеграла. Если
функция f(x) непрерывна
на отрезке [a,b],
то она интегрируема по этому отрезку.
Теорема
существования определённого интеграла. Если
функция f(x) непрерывна
на отрезке [a,b],
то она интегрируема по этому отрезку.
![]() Примем
это утверждение без доказательства,
поясним только его смысл. Интегрируемость
функции означает существование конечного
предела последовательности интегральных
сумм, т.е. такого числа
Примем
это утверждение без доказательства,
поясним только его смысл. Интегрируемость
функции означает существование конечного
предела последовательности интегральных
сумм, т.е. такого числа ,
что для любого
,
что для любого![]() найдётся
такое число
найдётся
такое число![]() ,
что как только разбиение отрезка
удовлетворяет неравенству
,
что как только разбиение отрезка
удовлетворяет неравенству![]() ,
то, независимо от выбора точек
,
то, независимо от выбора точек![]() выполняется
неравенство
выполняется
неравенство .
Требование непрерывностиf(x) достаточно
для интегрируемости, но не является
необходимым. Интегрируемы функции,
имеющие конечное или даже счётное число
точек разрыва на [a,b] при
условии их ограниченности (т.е. все точки
разрыва должны быть точками разрыва
первого рода). Неограниченная функция
не может быть интегрируемой (идея
доказательства этого утверждения:
если f(x) неограничена
на [a,b],
то она неограничена на каком-либо[xi-1
, xi],
т.е. на этом отрезке можно найти такую
точку
.
Требование непрерывностиf(x) достаточно
для интегрируемости, но не является
необходимым. Интегрируемы функции,
имеющие конечное или даже счётное число
точек разрыва на [a,b] при
условии их ограниченности (т.е. все точки
разрыва должны быть точками разрыва
первого рода). Неограниченная функция
не может быть интегрируемой (идея
доказательства этого утверждения:
если f(x) неограничена
на [a,b],
то она неограничена на каком-либо[xi-1
, xi],
т.е. на этом отрезке можно найти такую
точку ![]() ,
что слагаемое
,
что слагаемое![]() ,
а следовательно, и вся интегральная
сумма, будет больше любого наперед
заданного числа).
,
а следовательно, и вся интегральная
сумма, будет больше любого наперед
заданного числа).![]() Геометрический
смысл определённого интеграла.
Если f(x)
>0 на отрезке [a,b], то
Геометрический
смысл определённого интеграла.
Если f(x)
>0 на отрезке [a,b], то  равен
площади криволинейной трапецииABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x = a и x = b,
сверху – функцией y = f(x).
равен
площади криволинейной трапецииABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x = a и x = b,
сверху – функцией y = f(x).