§ 7. Эквивалентные функции

Пусть α(х) и β(х) — бесконечно малые приха. Их частное может и не быть бесконечно малым. Более того, предел отношения двух бесконечно малых величин является неопределенной величиной. В зависимости от того, какие конкретные бесконечно малые рассматриваются, этот символ может быть равен произвольному числу, или символу бесконечности.

Опр. 1.Если отношениедвух бесконечно малых величин само бесконечно мало, то α(х) называетсявеличиной более высокого порядка малости, чем β(х); при этом β(х) называется величиной более низкого порядка малости, чем α(х).

Если отношение двух бесконечно малых величин стремится к конечному пределу, не равному нулю, то α(х) и β(х) называютсябесконечно малыми одного порядка малости. В частности, если отношениедвух бесконечно малых величин стремится к 1, то α(х) и β(х) называютсяэквивалентными. В этом случае пишут α(х) ~ β (х).

Таблица эквивалентных бесконечно малых функций.Пусть α(х) - бесконечно малая прих0. Тогда

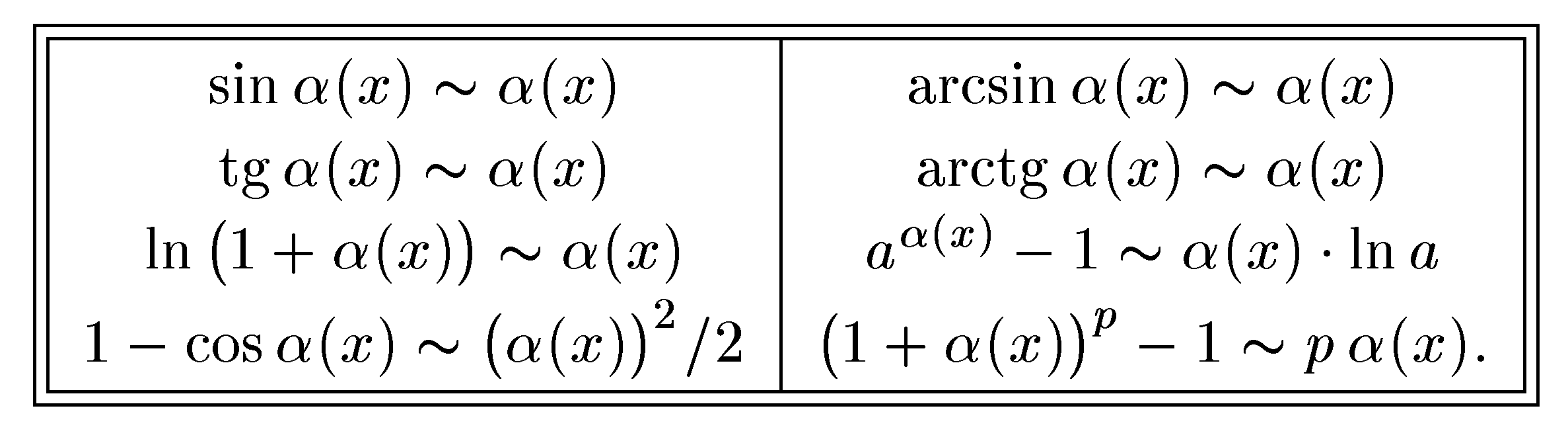
Принцип замены эквивалентных.Если функции α(х) и β(х) являются бесконечно малыми прихаи если α(х) ~(x), β (х) ~(x), то

§ 8. Односторонние пределы

Опр. 1. Если любая последовательность х_n→а, х_n<а (а–число или символ -∞) при любом , то говорят, что функцияf(x) при х→а-0 (слева) имеет левый односторонний предел Говорят, что функцияf(x) при х_n→а+0 (справа) имеет правый односторонний предел если функцияf(х) была определена правее точки а, и любая последовательность х_n→а, х_n>а (а–число или символ +∞) при любом .

Если f(х) имеет в точке а (а – число) односторонние пределы f(a-0) и f(a+0) и f(a-0)=f(a+0)=b (b – число или один из символов - ∞ или + ∞), тогда f(x) имеет в точке а обычный (двусторонний) предел Если односторонние пределы различны, т.е.f(a-0)≠f(a+0), то не существует предела функции при х→а.

§ 9. Непрерывность функции

Опр. 1. Функция f(x) называется непрерывной в точке а, если функция имеет конечный предел в точке а и этот предел совпадает со значением функции в этой точке, т. е.

Опр. 2. Функция называется непрерывной на промежутке X, если она непрерывна в каждой точке этого промежутка.

Теорема 1. Основные элементарные функции непрерывны в областях их определения.

§ 10. Точки разрыва функции

Пусть функция b₁ – левосторонний предел функции f(x) в точке х=а, b₂ – правосторонний предел функции f(x) в точке х=а. Рассмотрим функцию у=f(x), определенную на интервале X, кроме, быть может, точки . Точкаа называется точкой разрыва данной функции, если в ней функция определена, но не является непрерывной, или не определена в этой точке.

В зависимости от характера поведения функции в окрестности точки разрыва различают три основных вида разрывов.

Опр. 1. Точка а называется точкой устранимого разрыва функции f(x), если существует конечный , но либо функция не определена в точкеа, либо

Опр. 2. Разрыв I рода – в этом случае существуют конечные пределыи, ноВеличина |b₂–b₁| называется скачком.

Опр. 3. Разрыв II рода — в этом случае хотя бы один из пределов ине существует или бесконечен.