- •Министерство образования и науки
- •Раздел I. Введение в математический анализ
- •§ 1. Функция одной независимой переменной
- •§ 2. Основные свойства функций
- •§ 3. Числовая последовательность. Предел числовой последовательности
- •§ 4. Предел функции
- •§ 5. Бесконечно большие и бесконечно малые функции
- •§ 6. Замечательные пределы
- •§ 7. Эквивалентные функции
- •§ 8. Односторонние пределы
- •§ 9. Непрерывность функции
- •§ 10. Точки разрыва функции
- •Раздел IV. Производная и дифференциал
- •§ 1. Производная функции одной независимой переменной
- •§ 2. Правила дифференцирования функций
- •§ 3. Дифференциал. Геометрический смысл дифференциала
- •§ 3. Производные и дифференциалы высших порядков
- •§ 4. Применение дифференциала к приближенным вычислениям
- •Раздел V. Приложения производной
- •§ 1. Теоремы Ролля, Лагранжа, Коши
- •§ 2. Раскрытие неопределенностей по правилу Лопиталя
- •§ 3. Формула Тейлора
- •§ 4. Промежутки возрастания и убывания функций
- •§ 5. Экстремумы функций
- •§ 6. Наибольшее и наименьшее значения функции на отрезке
- •§ 7. Выпуклость и вогнутость функции. Точки перегиба
- •§ 8. Асимптоты
- •§ 9. Общий план исследования функций и построение графиков
- •Раздел VI. Комплексные числа
- •§ 1. Основные понятия
- •§ 2. Операции над комплексными числами в алгебраической форме
- •§ 3. Связь комплексных и действительных чисел. Геометрическая интерпретация комплексных чисел, модуль и аргумент комплексного числа, главное значение аргумента
- •§ 4. Тригонометрическая и показательная формы записи комплексного числа
- •§ 5. Решение квадратных уравнений, не имеющих действительных корней
- •Раздел VII. Неопределенный интеграл
- •§1. Первообразная. Неопределенный интеграл и его свойства
- •§ 2. Таблица основных интегралов
- •§ 3. Методы интегрирования
- •§ 4. Интегрирование рациональных дробей
- •§ 5. Интегрирование некоторых иррациональных и тригонометрических функций
- •Раздел VIII. Определённый интеграл
- •§ 1. Определенный интеграл. Геометрический смысл определённого интеграла.
- •Свойства определённого интеграла.
- •§ 2. Формула Ньютона-Лейбница.
- •§ 2. Интегрирование по частям и замена переменной в определенном интеграле
- •§ 3. Несобственные интегралы
- •Раздел IX. Дифференциальное исчисление функций нескольких переменных.
- •§ 1. Определение функции двух и более переменных
- •§ 2. Предел функции в точке. Непрерывность функции в точке и на множестве
- •§ 3. Частные производные. Полный дифференциал
- •§ 4. Производная по направлению и градиент функции двух переменных
- •§ 5. Экстремумы функций нескольких переменных.
- •Раздел X. Интегральное исчисление функций нескольких переменных.
- •§ 1. Двойной интеграл
- •§ 2. Криволинейные интегралы
- •Раздел XI. Дифференциальные уравнения
- •§1. Задачи, приводящие к дифференциальным уравнениям. Определение и основные понятия
- •§ 2. Дифференциальные уравнения первого порядка
- •§3. Дифференциальные уравнения 2-го порядка
- •Раздел XII. Ряды
- •§ 1.Числовые ряды: основные понятия
- •§ 2. Признаки сходимости числовых рядов
- •§ 3. Знакочередующиеся ряды
- •§ 4. Функциональные ряды
- •§ 5. Ряд Маклорена
- •§ 5. Методы разложения функций в ряд Тейлора
- •§ 7. Ряды Фурье
- •Раздел XIII. Теория функции комплексного переменного
- •§ 1. Функции комплексного переменного
- •§ 2. Дифференцируемость функции комплексной переменной.
§ 2. Дифференцируемость функции комплексной переменной.
Пусть w = f(z)
определена, однозначна и принимает
собственные значения в окрестности
точки z = x + iy ∈ C.
Производной функции w = f(z)
в точке z называется
предел ![]() .
Функция, имеющая конечную производную
в точкеz,
называется дифференцируемой в этой
точке.
В
этом определении важно, что стремление
Δz →
0 может проходить по любому пути. Как мы
увидим дальше, вследствие этого
обстоятельства существование
производной f’(z)
не сводится к существованию частных
производных функций u(x, y)
и v(x, y),
а требует некоторых дополнительных
условий. Сейчас мы дадим определение
основного в теории ФКП понятия
- аналитичности
функции в
точке и в области.
Опр.
Однозначная функция называется аналитической
(регулярной, голоморфной) в
точке z,
если она дифференцируема в некоторой
окрестности этой точки.
Однозначная
функция называется аналитической в
области D, если
она аналитична в каждой точке этой
области.
Примеры. 1. f(z)
= z 2. В
этом случае f (z +
Δz)
= (z +
Δz)2 = z 2 +
2 z·Δz +
(Δz) 2;
.
Функция, имеющая конечную производную
в точкеz,
называется дифференцируемой в этой
точке.
В
этом определении важно, что стремление
Δz →
0 может проходить по любому пути. Как мы
увидим дальше, вследствие этого
обстоятельства существование
производной f’(z)
не сводится к существованию частных
производных функций u(x, y)
и v(x, y),
а требует некоторых дополнительных
условий. Сейчас мы дадим определение
основного в теории ФКП понятия
- аналитичности
функции в
точке и в области.
Опр.
Однозначная функция называется аналитической
(регулярной, голоморфной) в
точке z,
если она дифференцируема в некоторой
окрестности этой точки.
Однозначная
функция называется аналитической в
области D, если
она аналитична в каждой точке этой
области.
Примеры. 1. f(z)
= z 2. В
этом случае f (z +
Δz)
= (z +
Δz)2 = z 2 +
2 z·Δz +
(Δz) 2; ![]() . Таким
образом , эта функция дифференцируема
в любой точке, и её производная равна
2z.
. Таким
образом , эта функция дифференцируема
в любой точке, и её производная равна
2z.
![]() 2.f(z)
= | z |2 = x2 + y2. Докажем,
что эта функция не имеет производной
ни в какой точке z ≠
0. Будем стремить Δz →
0 по двум путям: по прямой, параллельной
действительной оси Ох (в
этом случае Δz =
Δx),
и по прямой, параллельной мнимой оси Оу (в
этом случае Δz = i Δy).
В первом случае
2.f(z)
= | z |2 = x2 + y2. Докажем,
что эта функция не имеет производной
ни в какой точке z ≠
0. Будем стремить Δz →
0 по двум путям: по прямой, параллельной
действительной оси Ох (в
этом случае Δz =
Δx),
и по прямой, параллельной мнимой оси Оу (в
этом случае Δz = i Δy).
В первом случае ![]() ,во
втором
,во
втором ![]()
![]() . Эти
пределы равны, только если2х =
−2iy ⇒ х = y =
0. Таким образом, функция f(z)
= | z |2 = x2 + y2 может
быть дифференцируема в единственной
точке z =
0, во всех остальных точках пределы
. Эти
пределы равны, только если2х =
−2iy ⇒ х = y =
0. Таким образом, функция f(z)
= | z |2 = x2 + y2 может
быть дифференцируема в единственной
точке z =
0, во всех остальных точках пределы ![]() различны
в зависимости от способа стремления
Δz →
0, т.е.
различны
в зависимости от способа стремления
Δz →
0, т.е. ![]() не
существует.
Условия
Коши-Римана (Даламбера-Эйлера).
не
существует.
Условия
Коши-Римана (Даламбера-Эйлера).
Сейчас
мы сформулируем и докажем важнейшую в
теории ФКП теорему о необходимых и
достаточных условиях дифференцируемости
(а, следовательно, аналитичности)
функции.
Для
того, чтобы функция w = f(z)
= u(x, y)
+ i v(x, y)
была дифференцируема в точке z = x + iy,
необходимо и достаточно, чтобы
функции u(x, y)
= Re f(z) и v(x, y)
= Im f(z)
были дифференцируемы в точке (х,у), и
чтобы в этой точке выполнялись
соотношения 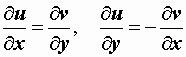 .
Доказательство. Необходимость. Здесь
мы применим идею, которой воспользовались,
когда доказывали, что функция f(z)
= | z |2 = x2 + y2 не
имеет производных в точках z ≠
0: подойдём к точке z двумя
путями - по направлениям Δz =
Δх (Δy =
0) и Δz = iΔy (Δx =
0).
В
первом случае: Δw =
(u(x +
Δx, y)
+ iv(x +
Δx, y))
− (u(x, y)
+ iv(x, y))
=
= (u(x +
Δx, y)
− u(x, y))
+ i(v(x +
Δx, y)
− v(x, y))
= Δxu + iΔxv;
.
Доказательство. Необходимость. Здесь
мы применим идею, которой воспользовались,
когда доказывали, что функция f(z)
= | z |2 = x2 + y2 не
имеет производных в точках z ≠
0: подойдём к точке z двумя
путями - по направлениям Δz =
Δх (Δy =
0) и Δz = iΔy (Δx =
0).
В
первом случае: Δw =
(u(x +
Δx, y)
+ iv(x +
Δx, y))
− (u(x, y)
+ iv(x, y))
=
= (u(x +
Δx, y)
− u(x, y))
+ i(v(x +
Δx, y)
− v(x, y))
= Δxu + iΔxv; ![]() .
Во
втором случае: (напомню, что
.
Во
втором случае: (напомню, что![]() )
Δw =
(u(x, y +
Δy)
+ iv(x, y +
Δy))
− (u(x, y)
+ iv(x, y))
=
= (u(x, y +
Δy)
− u(x, y))
+ i(v(x, y +
Δy)
− v(x, y))
= Δyu + iΔyv;
)
Δw =
(u(x, y +
Δy)
+ iv(x, y +
Δy))
− (u(x, y)
+ iv(x, y))
=
= (u(x, y +
Δy)
− u(x, y))
+ i(v(x, y +
Δy)
− v(x, y))
= Δyu + iΔyv; ![]() .
Пределы должны быть равны,
поэтому
.
Пределы должны быть равны,
поэтому![]() .
Достаточность. По
предположению теоремы, функции u(x, y), v(x, y)
дифференцируемы в точке (х,у),
поэтому
.
Достаточность. По
предположению теоремы, функции u(x, y), v(x, y)
дифференцируемы в точке (х,у),
поэтому ![]() где
α(Δx,
Δy),
β(Δx,
Δy)
- бесконечно малые более высокого порядка
по сравнению с
где
α(Δx,
Δy),
β(Δx,
Δy)
- бесконечно малые более высокого порядка
по сравнению с ![]() ,
т.е.
,
т.е.![]() ,
,![]() .
Найдём
.
Найдём![]() .
.![]()
![]() .
Последнее
слагаемое - бесконечно малая высшего
порядка по сравнению с
.
Последнее
слагаемое - бесконечно малая высшего
порядка по сравнению с
Δz = Δx + iΔy:
![]() ;
далее, в предыдущих слагаемых, пользуясь
формулами Коши-Римана, оставим только
частные производные по х,
т.е. заменим
;
далее, в предыдущих слагаемых, пользуясь
формулами Коши-Римана, оставим только
частные производные по х,
т.е. заменим ![]() на
на![]() ,
,![]() на
на![]() ;
тогда
;
тогда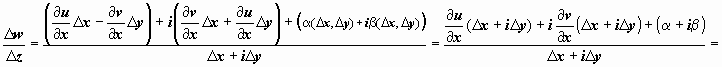
![]() .
Отсюда следует, что существует
.
Отсюда следует, что существует![]() ,
т.е. функция дифференцируема в точке
(х,у).
Производная
дифференцируемой функции может находиться
по любой из формул
,
т.е. функция дифференцируема в точке
(х,у).
Производная
дифференцируемой функции может находиться
по любой из формул ![]() ,
эти равенства следуют из условий
Коши-Римана. При вычислении производных
можно пользоваться всеми правилами
действительного анализа:
,
эти равенства следуют из условий
Коши-Римана. При вычислении производных
можно пользоваться всеми правилами
действительного анализа:
(в точках, где g(z) ≠ 0.
Примеры
вычисления производных.
1. Выше мы доказали, что функция f(z)
= z2имеет
производную, равную 2z,
в каждой точке. Проверим, что для этой
функции выполняются условия Коши-Римана.
Так какw = z2 =
(x + iy)2 = x2 - y2 +
2 ixy, то ![]() . Тогда
. Тогда![]() .
2.
Для функцииw = e z мы
получили u(x, y)
= e z cos y, v(x, y)
= e z sin y.
Поэтому
.
2.
Для функцииw = e z мы
получили u(x, y)
= e z cos y, v(x, y)
= e z sin y.
Поэтому ![]() ,
т.е. функция дифференцируема.
,
т.е. функция дифференцируема.![]() .Геометрический
смысл производной.
.Геометрический
смысл производной.
Равенство ![]() означает,
что Δw = f ′(z)·Δz +
γ(Δz)·Δz, где γ(Δz)
→ 0 при Δz →
0. Отсюда, в частности, следует, что если
функция дифференцируема в точке, то она
непрерывна в этой точке. Будем
писать Δw ≈ f ′(z)·Δz, пренебрегая
слагаемым высшего порядка малости.
Пусть в точке z существует f'(z)
≠ 0. Возьмём точки z и z +
Δz;
пусть w = f(z),
тогда Δw ≈
| f ′(z)|·e i arg f ′ (z)·Δz =
| f ′(z)|·|Δz|·e i (arg f ′ (z)
+ arg Δz).
Таким образом, |Δw|
в |f ′(z)| больше |Δz|,
arg Δw больше arg
Δz на arg f ′(z)для
любого arg Δz (с
точностью до бесконечно малых высшего
порядка). Следовательно, в окрестности
любой точки z,
в которой
означает,
что Δw = f ′(z)·Δz +
γ(Δz)·Δz, где γ(Δz)
→ 0 при Δz →
0. Отсюда, в частности, следует, что если
функция дифференцируема в точке, то она
непрерывна в этой точке. Будем
писать Δw ≈ f ′(z)·Δz, пренебрегая
слагаемым высшего порядка малости.
Пусть в точке z существует f'(z)
≠ 0. Возьмём точки z и z +
Δz;
пусть w = f(z),
тогда Δw ≈
| f ′(z)|·e i arg f ′ (z)·Δz =
| f ′(z)|·|Δz|·e i (arg f ′ (z)
+ arg Δz).
Таким образом, |Δw|
в |f ′(z)| больше |Δz|,
arg Δw больше arg
Δz на arg f ′(z)для
любого arg Δz (с
точностью до бесконечно малых высшего
порядка). Следовательно, в окрестности
любой точки z,
в которой
f ′(z)
≠ 0 отображение z → w = f (z) действует
следующим образом: любой вектор ![]() растягивается
в |f ′(z)| раз
и поворачивается на угол arg f ′(z).
растягивается
в |f ′(z)| раз
и поворачивается на угол arg f ′(z).
Конформность
дифференцируемого отображения.
Пусть
через точку z проходят
две гладкие кривые L1 и L2,
касательные l1 и l2 к
которым образуют с осью Ох углы,
соответственно, θ1 и θ2. Образы
этих кривых L'1 и L'2 при
дифференцируемом отображении z → w = f (z) имеют
касательные l1' и l2', образующие
с действительной осью Ou углы θ1' и θ2'. Согласно
предыдущему пункту,θ1' =
θ1 +
arg f '(z), θ2' =
θ2 +
arg f '(z), т.е. θ2' −
θ1' =
θ2 −
θ1. Таким
образом, дифференцируемое отображение
при f '(z)
≠ 0сохраняет углы между кривыми.
Сохраняется и направление отсчёта углов
(т.е. если θ2 >
θ1, то θ2' >
θ1').
Любое
преобразование плоскости в плоскость,
обладающее эти свойством (т.е. свойством
сохранения углов), называется конформным. Е![]() сли
при этом сохраняется направление отсчёта
углов, то преобразование называетсяконформным
преобразованием первого рода;
если направление отсчёта углов меняется
на противоположное, то преобразование
называется конформным
преобразованием второго рода.
Мы доказали, что аналитическая
в некоторой области G функция w = f(z) осуществляет
конформное отображение первого рода
во всех точках, в которых производная
отлична от нуля.
Пример
конформного отображения второго рода
– недифференцируемая функция
сли
при этом сохраняется направление отсчёта
углов, то преобразование называетсяконформным
преобразованием первого рода;
если направление отсчёта углов меняется
на противоположное, то преобразование
называется конформным
преобразованием второго рода.
Мы доказали, что аналитическая
в некоторой области G функция w = f(z) осуществляет
конформное отображение первого рода
во всех точках, в которых производная
отлична от нуля.
Пример
конформного отображения второго рода
– недифференцируемая функция ![]() .
.
Гармоничность
действительной и мнимой частей
аналитической функции. Дифференцируя
первое соотношение Коши-Римана ![]() по
переменнойх,
второе соотношение
по
переменнойх,
второе соотношение ![]() по
переменнойу,
получим
по
переменнойу,
получим 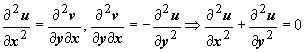 ,
т.е. Δu =
0 (Δ - оператор Лапласа), т.е. u(x, y)
- гармоническая функция. Дифференцируя
первое соотношение Коши-Римана по
переменной у,
второе соотношение по переменной х,
получим
,
т.е. Δu =
0 (Δ - оператор Лапласа), т.е. u(x, y)
- гармоническая функция. Дифференцируя
первое соотношение Коши-Римана по
переменной у,
второе соотношение по переменной х,
получим  ,
т.е. Δv =
0, т.е. v(x, y)
- тоже гармоническая функция. Пара
гармонических функций, связанных
соотношениями Коши-Римана,
называется сопряжёнными
функциями. Легко
доказать, что для любой гармонической
в односвязной области D функции u(x, y)
существует единственная (с точностью
до постоянного слагаемого) сопряжённая
с ней гармоническая функция v(x, y),
т.е. такая функция, чтоw = f(z)
= u(x, y)
+ i v(x, y)
- аналитическая функция; и наоборот, для
любой гармонической v(x, y)
существует сопряжённая с ней
гармоническая u(x, y).
Пусть, например, дана u(x, y),
обозначим
,
т.е. Δv =
0, т.е. v(x, y)
- тоже гармоническая функция. Пара
гармонических функций, связанных
соотношениями Коши-Римана,
называется сопряжёнными
функциями. Легко
доказать, что для любой гармонической
в односвязной области D функции u(x, y)
существует единственная (с точностью
до постоянного слагаемого) сопряжённая
с ней гармоническая функция v(x, y),
т.е. такая функция, чтоw = f(z)
= u(x, y)
+ i v(x, y)
- аналитическая функция; и наоборот, для
любой гармонической v(x, y)
существует сопряжённая с ней
гармоническая u(x, y).
Пусть, например, дана u(x, y),
обозначим ![]() .
Эти функции удовлетворяют условию
.
Эти функции удовлетворяют условию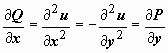 ,
т.е. векторное поле
,
т.е. векторное поле![]() потенциально.
Функциюv(x, y)
можно найти теперь из системы
потенциально.
Функциюv(x, y)
можно найти теперь из системы 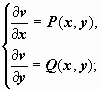 (как
это делается при решении уравнения в
полных дифференциалахP(x, y)·dx + Q(x, y)·dx =
0), и как потенциальную для поля
(как
это делается при решении уравнения в
полных дифференциалахP(x, y)·dx + Q(x, y)·dx =
0), и как потенциальную для поля ![]() функцию
функцию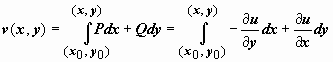 .
.
Пример восстановления аналитической функции по ее действительной (мнимой части). В качестве примера рассмотрим задачу, аналогичную задаче 5 из домашнего задания. Может ли функция v(x, y) = e -y(xcos x - ysin x) быть мнимой частью некоторой аналитической функции w = f(z)? В случае положительного ответа найти функцию w = f(z). Решение. Докажем, что v(x, y) - гармоническая функция. vx′ = e - y(cos x − x sin x − y cos x); vxx″ = e - y(−sin x − sin x − x cos x + y sin x) =
= e - y(−2 sin x − x cos x + y sin x); vy′ = −e - y(x cos x − y sin x + sin x);
vyy″ = e - y(x cos x − y sin x + sin x + sin x) =
=
e -
y(−2
sin x − x cos x + y sin x); 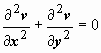 ,
т.е.v(x, y)
- гармоническая функция и, следовательно,
может являться мнимой частью аналитической
функции.
Найдём эту функцию. Для
действительной части u(x, y)
справедливы соотношения
,
т.е.v(x, y)
- гармоническая функция и, следовательно,
может являться мнимой частью аналитической
функции.
Найдём эту функцию. Для
действительной части u(x, y)
справедливы соотношения
|
|
|
для
нахождения φ(y)
используем второе уравнение
системы: ![]() φ ′(y)
= 0 ⇒ φ(y)
= C
=
const.
Формально
мы можем выписать w = f(z)
= u(x, y)
+ i v(x, y)
=
φ ′(y)
= 0 ⇒ φ(y)
= C
=
const.
Формально
мы можем выписать w = f(z)
= u(x, y)
+ i v(x, y)
=
=
e –y [-
(xsin x + ycos x)
+ i(xcos x - ysin x)] + C, но
толку в этой записи нет, так как не видна
зависимость f от z.
Поэтому сделаем по-другому. Выпишем
производную f ′(z): ![]() .
На действительной оси (приу=0,
т.е при z = x)
функция w = f(z)
превращается в функцию действительной
переменной f(x),
её производная - в f ′(x).
Положим в f ′(z) у =
0, x = z : f ′(z)|y =
0, z = x =
−e−y[(x cos x − y sin x +
sin x)
+ i(cos x − x sin x − y cos x)]|y =
0, z = x =
− z cos z −
sin z + i(cos z − z sin z);
проинтегрировав это выражение,
получим f(z).
Техника
нахождения неопределённых интегралов
в теории функций комплексной переменной
в основном та же, что и в математическом
анализе; таблица основных интегралов
в обоих случаях одинакова, поскольку
одинакова таблица производных.
Поэтому
.
На действительной оси (приу=0,
т.е при z = x)
функция w = f(z)
превращается в функцию действительной
переменной f(x),
её производная - в f ′(x).
Положим в f ′(z) у =
0, x = z : f ′(z)|y =
0, z = x =
−e−y[(x cos x − y sin x +
sin x)
+ i(cos x − x sin x − y cos x)]|y =
0, z = x =
− z cos z −
sin z + i(cos z − z sin z);
проинтегрировав это выражение,
получим f(z).
Техника
нахождения неопределённых интегралов
в теории функций комплексной переменной
в основном та же, что и в математическом
анализе; таблица основных интегралов
в обоих случаях одинакова, поскольку
одинакова таблица производных.
Поэтому ![]()
![]() =
−z sin z + iz cos z + C = iz (cos z + i sin z)
+ C = iz e iz + C, где С –
произвольная вещественная постоянная
интегрирования. Постоянная интегрирования
будет действительной, если по условию
задачи задана функция v(x, y),
и с точностью до произвольной постоянной
находится действительная
часть u(x, y) функции f(z); если
же задана функция u(x, y),
то с точностью до произвольной постоянной
интегрирования находится мнимая
часть v(x, y),
т.е постоянная будет чисто мнимым
числом Ci (C -
произвольное вещественное
число).
Проверим
полученный результат. Если f(z)
= iz e iz + C, то f(z)
= (ix − y) eix − y + C = = e−y(ix − y)(cos x + i sin x)
+ C = i e−y x cos x − e−y x sin x − e−y y cos x − i e−y y sin x + C =
=
−z sin z + iz cos z + C = iz (cos z + i sin z)
+ C = iz e iz + C, где С –
произвольная вещественная постоянная
интегрирования. Постоянная интегрирования
будет действительной, если по условию
задачи задана функция v(x, y),
и с точностью до произвольной постоянной
находится действительная
часть u(x, y) функции f(z); если
же задана функция u(x, y),
то с точностью до произвольной постоянной
интегрирования находится мнимая
часть v(x, y),
т.е постоянная будет чисто мнимым
числом Ci (C -
произвольное вещественное
число).
Проверим
полученный результат. Если f(z)
= iz e iz + C, то f(z)
= (ix − y) eix − y + C = = e−y(ix − y)(cos x + i sin x)
+ C = i e−y x cos x − e−y x sin x − e−y y cos x − i e−y y sin x + C = 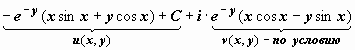 ;
;![]() ;
условия Коши-Римана выполнены,
следовательно, функцияf(z)
= iz e iz + C -
аналитическая на всей комплексной
плоскости функция.
Во
всех этих рассуждениях мы проигнорировали
вопрос о том, имеют ли функции u и v производные
порядка выше первого? (Существование
первых производных следует, как мы
видели, из дифференцируемости f(z)).
Дальше мы докажем, что, в отличие от
действительного случая, ФКП обладает
удивительным свойством - если она
аналитична в некоторой области (т.е. в
каждой точке этой области имеет первую
производную), то она бесконечно
дифференцируема в этой области (т.е. в
каждой точке этой области она имеет
производную любого порядка). Как
следствие, функции u и v тоже
бесконечно дифференцируемы.
;
условия Коши-Римана выполнены,
следовательно, функцияf(z)
= iz e iz + C -
аналитическая на всей комплексной
плоскости функция.
Во
всех этих рассуждениях мы проигнорировали
вопрос о том, имеют ли функции u и v производные
порядка выше первого? (Существование
первых производных следует, как мы
видели, из дифференцируемости f(z)).
Дальше мы докажем, что, в отличие от
действительного случая, ФКП обладает
удивительным свойством - если она
аналитична в некоторой области (т.е. в
каждой точке этой области имеет первую
производную), то она бесконечно
дифференцируема в этой области (т.е. в
каждой точке этой области она имеет
производную любого порядка). Как
следствие, функции u и v тоже
бесконечно дифференцируемы.