§ 4. Производная по направлению и градиент функции двух переменных

Опр. 1. Производная функции z=f(x;у) в направлении вектора вычисляется по формуле+, где,–направляющие косинусы вектора :=,=.

Если частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей, то производная в направлении вектора определяет скорость изменения функции в направлении вектора.

Опр. 2. Градиентом функции z=f(x;у) называется вектор

grad z=(,).

Свойства градиента:

1. Производная имеет наибольшее значение, если направление векторасовпадает с направлением градиента, причём это наибольшее значение производной равно.

2. Производная в направлении вектора, перпендикулярного градиенту, равна нулю.

§ 5. Экстремумы функций нескольких переменных.

Опр. 3. Пусть функция z=f(x;у) определена на множестве D и точка М(х;у)D. Если существует окрестность точки М, которая принадлежит множеству D, и для всех отличных от Мточек М выполняется неравенство f(М)<f(М₀) (f(М)>f(М₀)), то точку М называют точкой локального максимума (минимума) функции z=f(x;у), а число f(М₀) – локальным максимумом (минимумом) этой функции. Точки максимума и минимума функции называют её точками экстремума.

Теорема 1 (необходимые условия экстремума). Если функция z=f(x;у) в точке М(х;у) имеет локальный экстремум, то в этой точке частные производные ,равны нулю или не существуют.

Опр. 4. Точки, в которых ==0, называютсястационарными.

Опр. 5. Стационарные точки и точки, в которых частные производные не существуют, называются критическими.

Поэтому функция может достигать экстремальных значений только в критических точках; однако не всякая критическая точка является точкой экстремума.

Пусть в стационарной точке М(х;у) и некоторой её окрестности функция z=f(x;у) имеет непрерывные частные производные второго порядка. Введём обозначения:

А=(х;у), В=(х;у), С=(х;у), ∆=АС-В².

Теорема 2 (достаточные условия экстремума).

1. Если ∆>0, то функция z=f(x;у) в точке М имеет экстремум, причём максимум при А<0 и минимум при А>0.

2. Если ∆<0, то в точке М нет экстремума.

Для случая, когда количество переменных п>2, пользуются такой теоремой.

Теорема 3. Функция и= f(х;...;х) имеет минимум в стационарной точке М, если дифференциал второго порядка этой функции в точке М положителен d²f(М)>0, и максимум, если d²f(М)<0.

Раздел X. Интегральное исчисление функций нескольких переменных.

§ 1. Двойной интеграл

Рассмотрим в плоскости Оху замкнутую область D, ограниченную линией L. Разобьем эту область какими-нибудь линиями на n частей ∆S₁, ∆S₂,…, ∆S_n (причем теми же символами ∆S₁, ∆S₂,…, ∆S_n будем обозначать и площади соответствующих частей) и выберем в каждой части точку Р_i.

Пусть в области D задана функция z=f(x,y). Обозначим через f(P₁), f(P₂),…, f(P_n) значения этой функции в выбранных точках и составим сумму произведений вида f(P_i)ΔS_i : 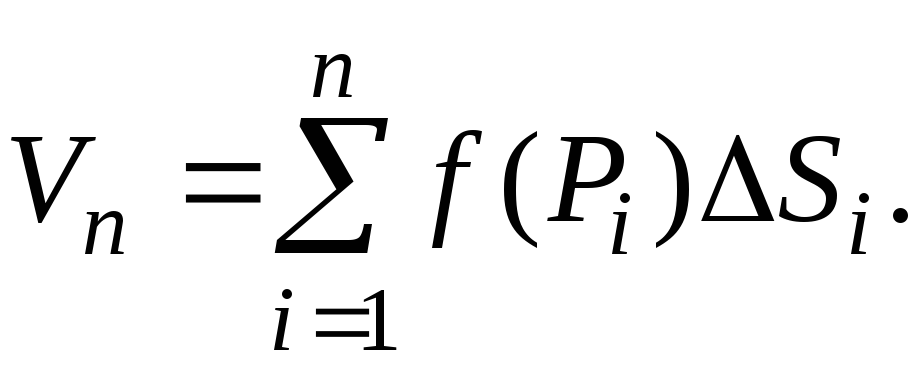(1)

Опр. 1. Сумма вида называетсяинтегральной суммой для функции f(x,y) в области D.

Замечание. 1. С геометрической точки зрения (при ) интегральная сумма (1) представляет собой сумму объемов цилиндров с основаниямиΔS_i и высотами f(P_i).

Опр. 2. Если существует один и тот же предел интегральных сумм (1) при n→∞ и max∆S_i→∞, не зависящий от способа разбиения области D и выбора точек P_i , то он называется двойным интегралом от функции f(x,y) по области D и обозначается 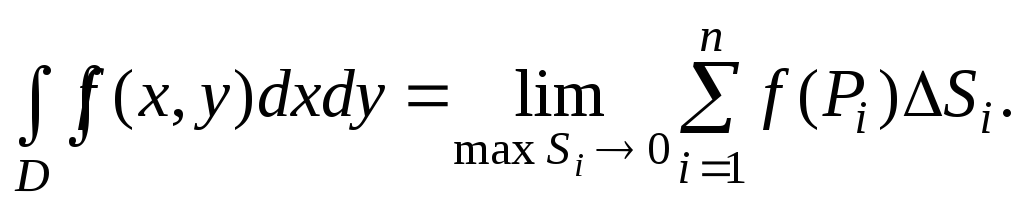ОбластьD при этом называется областью интегрирования.

Замечание 2. Для выяснения вопроса об условиях интегрируемости функции двух переменных можно по аналогии со случаем определенного интеграла ввести понятие верхней и нижней интегральных сумм, выбирая в каждой части области D точки, значение функции в которых является наибольшим и наименьшим для данной части. Тогда можно доказать, что необходимым и достаточным условием интегрируемости функции f(x,y) является, во-первых, ее ограниченность на D, а во-вторых, условие гдеi – некоторое разбиение, а S_i и s_i – соответственно верхняя и нижняя интегральные суммы.

Замечание 3. Если функция f(x,y) непрерывна на D, то она интегрируема по этой области.

Свойства двойных интегралов:

Часть свойств двойных интегралов непосредственно вытекает из определения этого понятия и свойств интегральных сумм, а именно:

1. Если функция f(x,y) интегрируема в D, то kf(x,y) тоже интегрируема в этой области, причем

2. Если в области D интегрируемы функции f(x,y) и g(x,y), то в этой области интегрируемы и функции f(x,y)±g(x,y), и при этом

3. Если для интегрируемых в области D функций f(x,y) и g(x,y) выполняется неравенство f(x,y)≤g(x,y), то

4. Если область D разбита на две области D₁ и D₂ без общих внутренних точек и функция f(x,y) непрерывна в области D, то

5. В случае интегрируемости на D функции f(x,y) в этой области интегрируема и функция |f(x,y)|, и имеет место неравенство

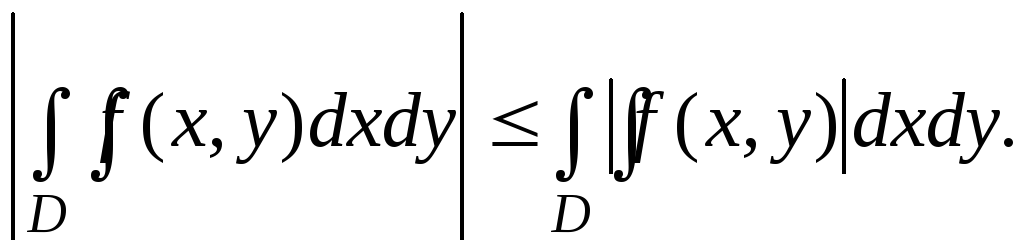
6. гдеS_D – площадь области D.

7. Если интегрируемая в области D функция f(x,y) удовлетворяет неравенству m≤f(x,y)≤M, то

Следствие (теорема о среднем).

В частности, при условии непрерывности функции f в D найдется такая точка этой области (х₀,у₀), в которой f(х₀,у₀)=μ, то есть