§ 3. Несобственные интегралы

п1. Несобственный интеграл по бесконечному промежутку.

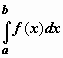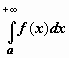Пусть функция f(x) определена на полуоси и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла приназывается несобственным интегралом функцииf(x) от a до и обозначается.Итак, по определению,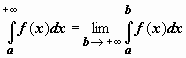. Если этот предел существует и конечен, интегралназывается сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.Примеры: 1. 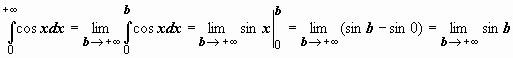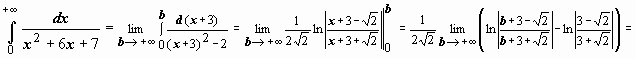; этот предел не существует; следовательно, исследуемый интеграл расходится.2.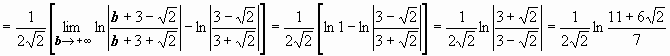; следовательно, интеграл сходится и равен.Аналогично интегралу с бесконечным верхним пределом интегрирования определяется интеграл в пределах отдоb : 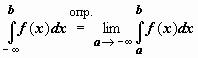и в пределах отдо:. В последнем случаеf(x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Пользуясь свойством аддитивности определённого интеграла, можно показать, что существование конечных пределов и их сумма не зависят от выбора точки c.  Примеры: 3. 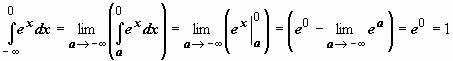. 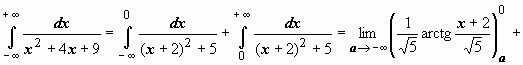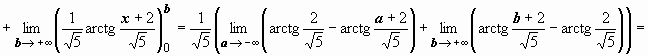Интеграл сходится.4.следовательно, интеграл сходится и равен.Очевидно следующее утверждение, которое мы сформулируем для интеграла с бесконечным верхним пределом:сходится тогда и только тогда, когда для любогоc, удовлетворяющего неравенству c > a, сходится интеграл 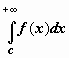(док-во: так как приa < c < b по свойству аддитивности , и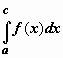отb не зависит, то конечный предел при для интеграла в левой части существует тогда и только тогда, когда существует конечный предел для интеграла в правой части равенства).Формула Ньютона-Лейбница для несобственного интеграла.

В приведённых примерах мы сначала вычисляли с помощью первообразной функции определённый интеграл по конечному промежутку, а затем выполняли предельный переход. Объединим два этих действия в одной формуле. Символом будем обозначать; символом- соответственно,; тогда можно записать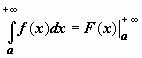,,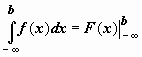, 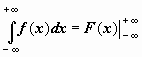подразумевая в каждом из этих случаев существование и конечность соответствующих пределов. 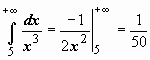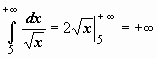Теперь решения примеров выглядят более просто:- интеграл сходится;- интеграл расходится.

Для несобственных интегралов применимы формулы интегрирования по частям и замены переменной: 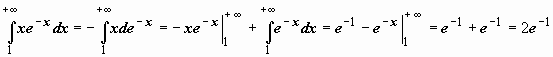; при замене переменной несобственный интеграл может преобразовываться в собственный. Так, например, вычислим интеграл:. Пусть,; если, то; еслито;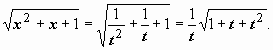Поэтому(это уже собственный интеграл) =.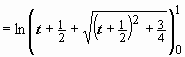

п2. Несобственный интеграл от неограниченной функции.  Пусть функция f(x) определена на полуинтервале (a, b], интегрируема по любому отрезку , и имеет бесконечный предел при. Несобственным интегралом отf(x) по отрезку [a, b] называется предел . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.Примеры: 17. 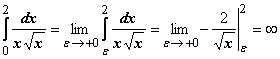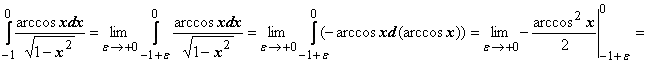- интеграл расходится;18.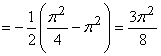- интеграл сходится.

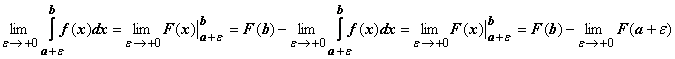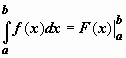Если для функции f(x) на полуинтервале (a, b] существует первообразная F(x), то, и сходимость интеграла определяется наличием или отсутствием конечного предела. Будем писать просто, имея в виду, что если соответствующий предел конечен, то интеграл сходится, в противном случае - расходится.Примеры: 19. (интеграл сходится).20.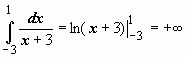(интеграл расходится).В следующих дальше случаях неограниченности функции будем поступать аналогично.

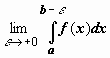Пусть функция f(x) определена на полуинтервале [a, b), интегрируема по любому отрезку , и имеет бесконечный предел при. Несобственным интегралом отf(x) по отрезку [a, b] называется предел . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.

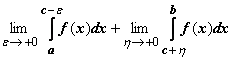Пусть функция f(x) определена на отрезке [a, b], имеет бесконечный предел при стремлении аргумента к какой-либо внутренней точке c этого отрезка: , интегрируема по любому отрезку, не содержащему точкуc. Несобственным интегралом от f(x) по отрезку [a,b] называется . Интеграл сходится, если оба эти пределы существуют и конечны, в противном случае интеграл расходится.