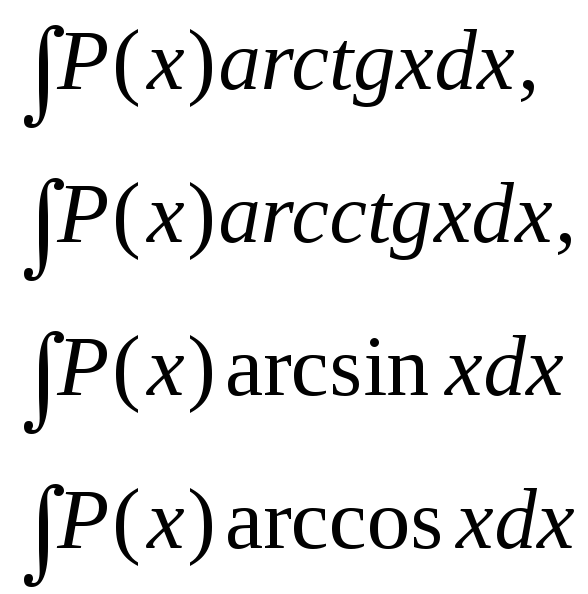- •Министерство образования и науки
- •Раздел I. Введение в математический анализ
- •§ 1. Функция одной независимой переменной
- •§ 2. Основные свойства функций
- •§ 3. Числовая последовательность. Предел числовой последовательности
- •§ 4. Предел функции
- •§ 5. Бесконечно большие и бесконечно малые функции
- •§ 6. Замечательные пределы
- •§ 7. Эквивалентные функции
- •§ 8. Односторонние пределы
- •§ 9. Непрерывность функции
- •§ 10. Точки разрыва функции
- •Раздел IV. Производная и дифференциал
- •§ 1. Производная функции одной независимой переменной
- •§ 2. Правила дифференцирования функций
- •§ 3. Дифференциал. Геометрический смысл дифференциала
- •§ 3. Производные и дифференциалы высших порядков
- •§ 4. Применение дифференциала к приближенным вычислениям
- •Раздел V. Приложения производной
- •§ 1. Теоремы Ролля, Лагранжа, Коши
- •§ 2. Раскрытие неопределенностей по правилу Лопиталя
- •§ 3. Формула Тейлора
- •§ 4. Промежутки возрастания и убывания функций
- •§ 5. Экстремумы функций
- •§ 6. Наибольшее и наименьшее значения функции на отрезке
- •§ 7. Выпуклость и вогнутость функции. Точки перегиба
- •§ 8. Асимптоты
- •§ 9. Общий план исследования функций и построение графиков
- •Раздел VI. Комплексные числа
- •§ 1. Основные понятия
- •§ 2. Операции над комплексными числами в алгебраической форме
- •§ 3. Связь комплексных и действительных чисел. Геометрическая интерпретация комплексных чисел, модуль и аргумент комплексного числа, главное значение аргумента
- •§ 4. Тригонометрическая и показательная формы записи комплексного числа
- •§ 5. Решение квадратных уравнений, не имеющих действительных корней
- •Раздел VII. Неопределенный интеграл
- •§1. Первообразная. Неопределенный интеграл и его свойства
- •§ 2. Таблица основных интегралов
- •§ 3. Методы интегрирования
- •§ 4. Интегрирование рациональных дробей
- •§ 5. Интегрирование некоторых иррациональных и тригонометрических функций
- •Раздел VIII. Определённый интеграл
- •§ 1. Определенный интеграл. Геометрический смысл определённого интеграла.
- •Свойства определённого интеграла.
- •§ 2. Формула Ньютона-Лейбница.
- •§ 2. Интегрирование по частям и замена переменной в определенном интеграле
- •§ 3. Несобственные интегралы
- •Раздел IX. Дифференциальное исчисление функций нескольких переменных.
- •§ 1. Определение функции двух и более переменных
- •§ 2. Предел функции в точке. Непрерывность функции в точке и на множестве
- •§ 3. Частные производные. Полный дифференциал
- •§ 4. Производная по направлению и градиент функции двух переменных
- •§ 5. Экстремумы функций нескольких переменных.
- •Раздел X. Интегральное исчисление функций нескольких переменных.
- •§ 1. Двойной интеграл
- •§ 2. Криволинейные интегралы
- •Раздел XI. Дифференциальные уравнения
- •§1. Задачи, приводящие к дифференциальным уравнениям. Определение и основные понятия
- •§ 2. Дифференциальные уравнения первого порядка
- •§3. Дифференциальные уравнения 2-го порядка
- •Раздел XII. Ряды
- •§ 1.Числовые ряды: основные понятия
- •§ 2. Признаки сходимости числовых рядов
- •§ 3. Знакочередующиеся ряды
- •§ 4. Функциональные ряды
- •§ 5. Ряд Маклорена
- •§ 5. Методы разложения функций в ряд Тейлора
- •§ 7. Ряды Фурье
- •Раздел XIII. Теория функции комплексного переменного
- •§ 1. Функции комплексного переменного
- •§ 2. Дифференцируемость функции комплексной переменной.
Раздел VII. Неопределенный интеграл
§1. Первообразная. Неопределенный интеграл и его свойства
Опр.
1. Функция
![]() называетсяпервообразной
для функции
называетсяпервообразной
для функции
![]() если производная от функции
если производная от функции![]() равна
равна![]() :
:![]()
Отыскание
первообразной функции по заданной ее
производной
![]() есть действие обратное дифференцированию
–интегрирование.
есть действие обратное дифференцированию
–интегрирование.
Если
функция
![]() имеет первообразную
имеет первообразную![]() ,
то и все функции вида
,
то и все функции вида![]() будут для нее первообразными, т.к.
будут для нее первообразными, т.к.
![]()
Опр.
2. Совокупность
функций
![]() первообразных для функции
первообразных для функции![]() называетсянеопределенным
интегралом
и обозначается символом:
называетсянеопределенным
интегралом
и обозначается символом:
![]() если
если![]() где
где![]() –подынтегральная
функция;
–подынтегральная
функция;
![]() –подынтегральное
выражение;
х
– переменная
интегрирования;
С – произвольная
постоянная
неопределенного интеграла.
–подынтегральное
выражение;
х
– переменная
интегрирования;
С – произвольная
постоянная
неопределенного интеграла.
Свойства неопределенного интеграла.
Неопределенный интеграл дифференциала функции равен этой функции, сложенной с произвольной постоянной:
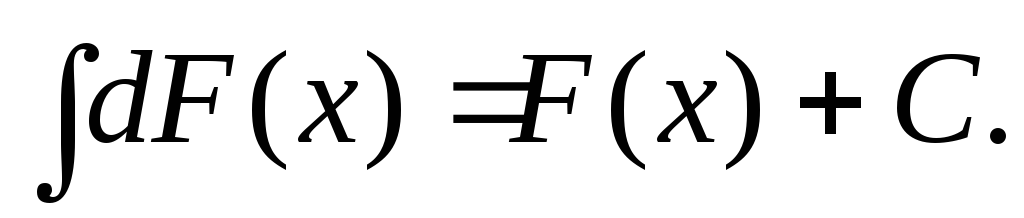
Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций:
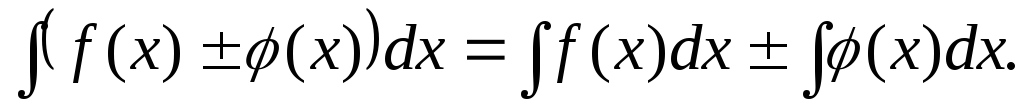
Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла:
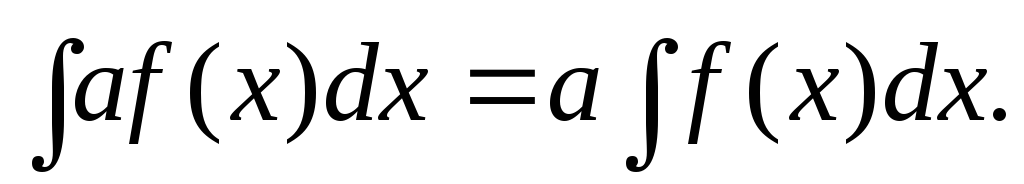
§ 2. Таблица основных интегралов
Замечания:
В вышеперечисленных формулах а, b, k – постоянные, х – независимая переменная.
При применении формул 3, 4, 5 знак абсолютной величины (модуля) пишется только в тех случаях, когда выражение, стоящее под знаком логарифма, может иметь отрицательное значение.
§ 3. Методы интегрирования
п. 1. Непосредственное интегрирование
Непосредственное интегрирование производится путем применения соответствующего табличного интеграла. Здесь могут представиться следующие случаи:
данный интеграл находится непосредственно по соответствующему табличному интегралу;
данный интеграл после применения свойств 2 и 3 приводится к одному или нескольким табличным интегралам;
данный интеграл после элементарных тождественных преобразований над подынтегральной функцией и применения свойств 2 и 3 приводится к одному или нескольким табличным интегралам.
п. 2. Интегрирование подстановкой
Метод
замены переменной (метод подстановки)
состоит в том, что при вычислении
интеграла
![]() вместо переменнойх
вводится новая переменная t
по формуле
вместо переменнойх
вводится новая переменная t
по формуле
![]() причем
причем![]() подбирается так, чтобы после подстановки
получалась подынтегральная функция
более удобная для интегрирования. При
этом справедлива формула:
подбирается так, чтобы после подстановки
получалась подынтегральная функция
более удобная для интегрирования. При
этом справедлива формула:
![]()
После того как интеграл с новой переменной t будет найден, посредством подстановки t=ψ(x) он приводится к переменной х.
п. 3. Внесение под знак дифференциала
Заметим,
что формулу из предыдущего пункта часто
применяют справа налево, т.е. записывают
в виде:
![]()
Как
видно из формулы под знак дифференциала
вносится некоторая функция
![]()
Если
![]() – первообразная для
– первообразная для![]() то получаем:
то получаем:
![]()
В
частном случае, если
![]() то
то![]() имеем:
имеем:

п. 4. Интегрирование по частям
Интегрируя
обе части равенства интеграла произведения
![]() получим:
получим:
![]()
откуда
![]()
Вычисление
интеграла
![]() сводится к вычислению интеграла
сводится к вычислению интеграла![]() ,
если последний будет проще исходного.
,
если последний будет проще исходного.
Укажем некоторые классы интегралов, которые вычисляются методом интегрирования по частям:
|
Интеграл |
Заменяемая функция |
|
где Р(х)—многочлен. |
|
|
|
|
|
|
|
|
|
|
|
|
u – обратная тригонометрическая функция |
|
|
Нужно дважды применить формулу интегрирования по частям, за u взять оба раза либо показательную, либо тригонометрическую функцию |