§ 3. Связь комплексных и действительных чисел. Геометрическая интерпретация комплексных чисел, модуль и аргумент комплексного числа, главное значение аргумента

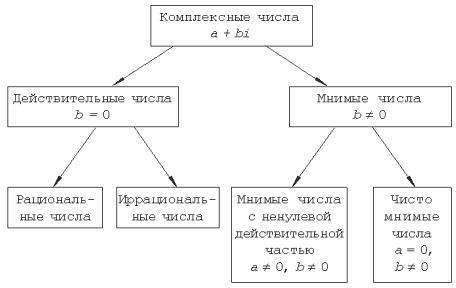
Классификация комплексных чисел:

Комплексные числа можно изображать на плоскости. Так число (1) изображается в прямоугольной системе координат точкой М(a;b).

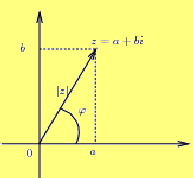
Такая плоскость называется комплексной плоскостью переменной z, ось Ох называется действительной, а ось Оу – мнимой.

При у=0 комплексное число является одновременно действительным числом. Поэтому действительные числа являются отдельным случаем комплексных, они изображаются на оси Ох.

Комплексные числа z=iy, в которых х=0, называются чисто мнимыми; такие числа изображаются на оси Оу.

Опр. Полярные координаты точки М(х;у) на комплексной плоскости называются модулем и аргументом комплексного числа и обозначаются

§ 4. Тригонометрическая и показательная формы записи комплексного числа

Поскольку , то по формуле (1) имеем. Это выражение называетсятригонометрической формой комплексного числа z.

Модуль комплексного числа определяется однозначно, а аргумент – с точностью до 2:.

Здесь -общее значение аргумента, а -главное значение аргумента, которое находится на промежутке [0;и отсчитывается от осиОх против часовой стрелки.

Если , то считают, чтоа- неопределён.

Известно, что показательную функцию с мнимым показателем можно выразить через тригонометрические функции по формуле Эйлера . Отсюда следует, что всякое комплексное число можно записать в форме, которая называетсяпоказательной формой комплексного числа z.

Рассмотрим действия над комплексными числами в тригонометрической форме.

Пусть ,. Тогда

=

Значит, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило распространяется на произвольное конечное число множителей. В частности,

.

Последняя формула называется формулой Муавра.

При делении комплексных чисел имеем

.

Рассмотрим извлечение корня из комплексного числа. Если для данного комплексного числа надо найти кореньп-й степени , то по определению корня и формуле Муавра имеем

.

Отсюда ,.

Поскольку r и положительные, то, где под корнем понимают его арифметическое значение. Поэтому

.

Давая k значения 0,1,2,…, п -1, получим п разных значений корня. Для других значений k аргументы будут отличаться от найденных на число, кратное 2, поэтому значения корня будут совпадать с уже найденными.

§ 5. Решение квадратных уравнений, не имеющих действительных корней

Одна из причин введения комплексных чисел состояла в том, чтобы добиться разрешимости любого квадратного уравнения, в частности уравнения x² = – 1, которое имеет два решения: x₁ = i, x₂ = – i.

Перейдем теперь к вопросу о решении полного квадратного уравнения. Напомним, что квадратным уравнением называют уравнение вида: ax²+bx+c=0 (a≠0), где x – неизвестная, a, b, c – действительные числа, соответственно первый, второй коэффициенты и свободный член. Для решения таких уравнений надо найти D=b²–4ac. Если

Значение дискриминанта D=b2–4ac	Корни уравнения
D>0	Уравнение имеет два различных действительных корня
D=0	Уравнение имеет два равных действительных корня
D<0	Уравнение имеет два различных мнимых корня

Итак, введение комплексных чисел позволяет разработать полную теорию квадратных уравнений.