

121
Например:
1)
.
2)
.
5. Неопределенность типа |
|
в отношении трансцендентных функций при |
. |
|
Такие неопределенности обычно раскрываются с помощью таблицы замечательных эквивалентностей. Например:
|
|
|
|
при |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Неопределенность типа |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Эти неопределенности преобразуются к неопределенностям типа |
|
или |
|
. |
||||||||||||||||
|
|
|||||||||||||||||||
|
Например: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
7. Вычисление пределов степенно-показательных выражений.
|
Степенно-показательной функцией называется функция |
, где |
|
, |
элементарные функции, |
. Функция |
также является |
элементарной, т.к. она представима в виде композиции элементарных функций:
е |
. |
|
|
Пусть существуют пределы: |
, |
. |
|
122
1) если |
, то |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||
2) если |
, то возможны следующие варианты: |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
неопределенность типа |
. |
|
|
|
|
|
|
|
|
|||||||||
3) если |
|
и |
, то: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
, |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
||||
|
|
|
, |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|||
4) если |
|
и |
, то: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
, |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|||
|
|
|
, |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
неопределенность типа |
. |
|
|
|||||||||||||
5) если |
|
и |
, то: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
неопределенность типа |
. |
|
|
||||||||||||
Таким образом, получаем три новых типа неопределенностей, связанных со |
||||||||||||||||||||||
степенно-показательной функцией |
: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
, |
, |
. |
|
|
|
|
|
|
|
|
|
|
|||||||
Примером раскрытия неопределенностей типа |
|
|
|
является второй |
||||||||||||||||||
замечательный предел: |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Выведем следующую формулу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Формула доказана. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например: |
|
|
; |
|
|
|
|
; |
|
|
|
. |
||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||
Неопределенности типа |
и |
|
изучаются в разделе «Дифференциальное |
|||||||||||
исчисление» |
курса математического анализа. |
|
|
|
|
|
|
|||||||
123
§ 11. Признаки существования предела функции.
Существование предела монотонной и ограниченной функции.
Для монотонных функций справедливы утверждения о существовании пределов, аналогичные утверждениям для монотонных последовательностей (см. § 9 главы 3).
Пусть функция |
имеет область определения |
и |
точка сгущения |
(при этом точка может принадлежать или нет). Введем обозначения: |
|||
, где |
произвольное число, |
; |
|
, где |
произвольное число, |
. |
|
Справедливы следующие утверждения. |
|
|
|
||||
Теорема 1. |
Если функция |
возрастает в некоторой проколотой окрестности |
и |
||||
ограничена сверху на этой окрестности, то существует конечный предел |
|
. |
|||||
Если функция |
возрастает в некоторой проколотой окрестности |
|
и не |
||||
ограничена сверху на этой окрестности, то |
|
. |
|
|
|||
Теорема 2. |
Если функция |
убывает в некоторой проколотой окрестности |
|
и |
|||
ограничена снизу на этой окрестности, то существует конечный предел |
|
. |
|||||
Если функция |
убывает в некоторой проколотой окрестности |
и не |
|||||
ограничена снизу на этой окрестности, то |
|
. |
|
|
|||
Теорема 3. |
Если функция |
возрастает в некоторой проколотой окрестности |
и |
||||
ограничена снизу на этой окрестности, то существует конечный предел |
|
. |
|||||
Если функция |
возрастает в некоторой проколотой окрестности |
|
и не |
||||
ограничена снизу на этой окрестности, то |
|
. |
|
|
|||
Теорема 4. |
Если функция |
убывает в некоторой проколотой окрестности |
|
и |
|||
ограничена сверху на этой окрестности, то существует конечный предел |
|
. |
|||||
Если функция |
убывает в некоторой проколотой окрестности |
и не |
|||||
ограничена сверху на этой окрестности, то |
|
. |
|
|
|||
Аналогичные утверждения справедливы и при |
. |
|
|
||||
Общий признак существования предела. |
|
|
|
|
|||
Для произвольных функций |
имеется такой же признак существования |
||||||
предела, как и в случае последовательности (см. § 10 главы 3). |
|
|
|
||||
Теорема 5 (признак Больцано-Коши при |
). |
|
|
|
|||
Пусть |
точка сгущения . Для того чтобы функция |
имела предел при |
|||||
, необходимо и достаточно, чтобы |
|
|
|
|
|||
|
|
|
|
|
|
|
. |
Аналогичное утверждение справедливо и при |
. |
|
|
||||
124
Теорема 6 (признак Больцано-Коши при |
). |
|
|
||
Пусть |
точка сгущения (см. § 1). Для того чтобы функция |
имела |
|||
предел при |
, необходимо и достаточно, чтобы |
|
|
||
|
|
|
|
|
. |
Аналогичное утверждение справедливо и при |
. |
|
|||
Доказательство этих теорем можно найти, например в |
и . |
|
|||
125
Глава 5. Непрерывность функции.
Содержание
§1. Понятие непрерывности функции…………………………………………………. 126
§2. Классификация точек разрыва………………………………………………..……. 128
§3. Свойства функций, непрерывных в точке…..…………………………………. 130
§4. Свойства функций, непрерывных на отрезке …………………………….…. 131
§5. Монотонность и непрерывность функций …………..………………………… 136
§6. Понятие равномерной непрерывности .....…………………………………….. 138
126
§ 1. Понятие непрерывности функции.
Дана функция |
с областью определения |
. Пусть |
точка сгущения |
|||
множества |
и |
. Тем самым предполагаем, что в любой окрестности точки |
||||
имеется бесконечно много точек множества , отличных от , и в самой точке |
||||||
функция |
определена, т.е. принимает некоторое значение |
. |
||||
Сформулируем следующие равносильные определения непрерывности функции |
||||||
в точке . |
|
|
|
|
|
|
Определение 1. |
Функция |
называется непрерывной в точке |
, если |
|||
|
|
|
|
. |
|
|
Из определения следует, что для непрерывной функции в точке знак функции и |
||||||
знак предела можно переставлять местами: |
|
|
||||
|
|
|
|
. |
|
|
Определение 2. |
Функция |
называется непрерывной в точке |
, если |
|||
|
|
0 |
: |
, |
|
. |
Определение 3. |
Функция |
называется непрерывной в точке |
, если |
|||
|
|
|
: |
|
. |
|
Заметим, что в этих определениях нет условия |
или |
. |
||||
Для следующего определения введем понятия приращений аргумента и функции. |
||||||
Пусть |
|
, тогда величину |
называют приращением аргумента |
|||
(приращением независимой переменной) в точке , а величину |
называют |
|||||
приращением функции (приращением зависимой переменной) в точке :
-приращение аргумента;
-приращение функции.
Приращения аргумента и функции могут принимать любые значения (положительные, отрицательные или нулевые).
Определение 4. Функция |
называется непрерывной в точке , если |
|
|
при |
. |
Это означает, что для непрерывной функции в точке бесконечно малым приращениям аргумента соответствуют бесконечно малые приращения функции, т.е. при незначительных изменениях аргумента значения функции также изменяются незначительно .
Определение 5. Функция |
называется непрерывной в точке |
, если |
, |
и |
. |
Если функция не является непрерывной в точке, то она называется разрывной в этой точке, при этом точка называется точкой разрыва функции.
|
|
|
127 |
Если |
, то функция называется непрерывной слева в точке ; если |
||
|
, то функция называется непрерывной справа в точке . |
|
|
Функция |
называется непрерывной на множестве |
, если она |
|
непрерывна в каждой точке этого множества. |
|
|
|
Если |
замкнутый промежуток, то непрерывность на |
означает |
|
непрерывность в каждой внутренней точке этого промежутка, а на концах промежутка соответственно непрерывность справа (в точке ) и слева (в точке ).
График непрерывной функции представляет собой непрерывную кривую. Все основные (и не только) элементарные функции являются непрерывными функциями в каждой точке из области определения.
Теорема (о непрерывности элементарных функций). |
|
|
Если |
элементарная функция и , то |
непрерывна в точке . |
Доказательство. По теореме о пределе элементарной функции (см. §5 главы 4) имеем:
|
|
|
|
, а это и означает, что |
непрерывна в точке . |
|
|
|||||||||||
Замечание 1. Пусть |
|
точка сгущения множества |
, но |
, т.е. значение |
||||||||||||||
не определено. Если при этом |
|
, то функцию |
можно доопределить |
|||||||||||||||
так, чтобы новая функция стала непрерывной в точке |
: |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
непрерывна в точке . При этом обычно говорят, что |
|||||||||||
непрерывна в точке |
, подразумевая на самом деле непрерывность |
. |
||||||||||||||||
Например, функция |
|
|
|
|
не определена в точке |
, но |
|
|
. |
|||||||||
|
|
|
|
|
|
|||||||||||||
Поэтому новая функция |
|
|
|
|
|
непрерывна в точке , но если |
||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
, где |
, то |
разрывна в точке . |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||
Замечание 2. Пусть |
|
точка сгущения множества |
, но |
, т.е. значение |
||||||||||||||
не определено. Если |
|
|
|
|
|
не существует, то как бы ни доопределяли функцию |
||||||||||||
в точке , новая функция будет разрывной в этой точке: |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
разрывна в точке . При этом обычно говорят, что |
|||||||||||
разрывна в точке |
, подразумевая на самом деле разрывность |
. |
|
|||||||||||||||
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) Функция |
|
|
не определена в точке |
и не |
|
|
. Поэтому новая функция |
|||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
разрывна в точке |
(см. ниже график). |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
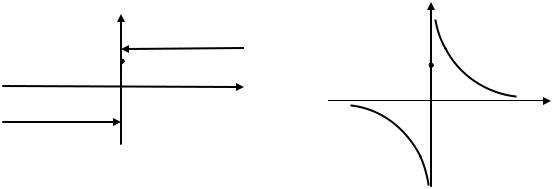
128
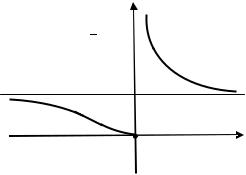
2) Функция |
|
|
не определена в точке и не |
|
. Поэтому новая функция |
||||||
|
|
|
|||||||||
|
|
|
|
|
разрывна в точке (см. ниже график). |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 2. |
Классификация точек разрыва. |
||
|
Дана функция |
с областью определения и |
точка сгущения области . |
|
Пусть |
точка разрыва функции |
. Различают три типа точек разрыва: |
||
1)точка устранимого разрыва;
2)точка разрыва 1-го рода;
3)точка разрыва 2-го рода.
Рассмотрим подробнее эти типы точек разрыва.
1. Точка является точкой устранимого разрыва, если |
. |
||
Например, для функции |
|
точка является точкой устранимого |
|
|
|
||
разрыва, т.к. |
. |
|
|
Название точка устранимого разрыва происходит от возможности устранить
разрыв путем переопределения (доопределения) функции в указанной точке.
Например, если в рассмотренном примере значение функции |
|
изменить в |
||||||
точке разрыва |
со значения 2 на значение 1, то новая функция станет непрерывной в |
|||||||
указанной точке: |
|
|
|
непрерывна в точке . |
|
|
||
|
|
|
|
|
||||
2. Точка |
является точкой разрыва 1-го рода, если |
|
|
|||||
|
, |
|
|
|
и |
. |
|
|
При этом разность |
|
|
|
- называют скачком функции |
в точке . |
|||
Например, для функции |
|
|
|
точка |
является точкой разрыва 1-го рода, |
|||
|
|
|
||||||
т.к. |
|
; при этом скачок функции в точке 0 равен: |
|
|
||||
|
(см. график). |
|
|
|
||||
3. Точка |
является точкой разрыва 2-го рода, если |
- не существует, |
||||||

|
|
|
|
|
|
|
129 |
т.е. хотя бы один из пределов |
|
|
или |
не существует (или равен ). |
|||
Например, для функции |
|
|
точка |
является точкой разрыва 2-го рода, |
|||
|
|
||||||
т.к. |
, |
|
|
(см. график). |
|
||
И для функции |
|
|
|
|
|
точка также является точкой разрыва 2-го |
|
|
|
|
|
|
|||
рода, т.к. |
- не существует (см. §1 главы 4). |
||||||
Замечание.
Точки разрыва 1-го и 2-го рода можно разделять на точки разрыва справа и слева.
Например, если |
, но не |
, то |
точка разрыва 1-го рода слева и |
|
точка разрыва 2-го рода справа; если при этом |
|
, то |
точка |
|
непрерывности слева. |
|
|
|
|
Пример 1.
|
Здесь |
- точка разрыва 1-го рода слева и точка разрыва 2-го рода справа. |
|||||||||||||||||||||||
Пример 2. |
|
|
|
|
|
|
. Эта функция является элементарной функцией, поэтому она |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
непрерывна в любой точке |
. |
Так как |
|
, то в этой точке функцию можно |
|||||||||||||||||||||
доопределить любым значением |
|
|
|
|
. После этого можно исследовать функцию на |
||||||||||||||||||||
непрерывность в точке |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Вычислим односторонние пределы. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Таким образом, функция имеет в точке |
разрыв 1-го рода; |
|
||||||||||||||||||||||
при этом скачок функции в точке 0 равен: |
|
|
|
. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
Пример 3. |
|
|
|
|
|
|
|
. Функция |
|
|
является элементарной функцией, поэтому |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
она непрерывна в любой точке |
|
|
. Так как |
|
|
|
|
|
при |
, то функция |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
также непрерывна в любой точке |
. |
Исследуем функцию |
на непрерывность в |
||||||||||||||||||||||
точке |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим односторонние пределы. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
;
|
|
|
|
|
|
130 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||
Функция |
имеет в точке |
разрыв справа 2-го рода; так как |
и |
|||
, то функция |
|
непрерывна слева в точке . |
|
|||
Таким образом, функция |
в точке имеет непрерывность слева и разрыв 2-го |
|||||
рода справа (см. график).
§ 3. Свойства функций, непрерывных в точке.
Арифметические операции над непрерывными функциями.
Теорема 1. Если функции |
и |
непрерывны в точке , то в этой точке |
|
|||||
непрерывны также их сумма и разность |
, произведение |
и |
|
|||||
частное |
|
(при условии, что в случае частного |
). |
|
|
|||
|
|
|
||||||
Доказательство. По определению непрерывности функций |
и |
в точке |
имеем: |
|||||
|
|
и |
|
. Используя арифметические действия с пределами |
||||
(см. §4 главы 4) при |
|
, получим: |
|
|
|
|
||
|
|
|
|
|
. Это и означает непрерывность |
|||
функций |
|
|
в точке |
. Аналогично для произведения и частного этих функций. |
||||
Об ограниченности непрерывной функции. |
|
|
|
|||||
Теорема 2. Если функция |
непрерывна в точке , то она и ограничена в некоторой |
|||||||
окрестности точки . |
|
|
|
|
|
|||
Доказательство. Так как |
|
, то согласно одному из свойств пределов |
||||||
(см. свойство 4 из §2 главы 4) существует окрестность |
точки |
, в которой функция |
||||||
ограничена: |
|
|
для некоторого числа |
. Это и означает |
||||
ограниченность функция |
в некоторой окрестности точки . |
|
|
|||||
О сохранении знака непрерывной функции. |
|
|
|
|||||
Теорема 3. Если функция |
непрерывна в точке и |
, то и в некоторой |
||||||
окрестности точки |
значения |
и имеют такой же знак, какой у значения |
. |
|||||
