ИЭ / 1 семестр / Учебники / Введение в мат.анализ

Дана функция

с областью определения

. Пусть

точка сгущения

множества (см. §10 главы 1). При этом точка

может принадлежать

или нет.

Представляет интерес поведение функции

при приближении к точке .

Определение 1 (по Коши или на языке -

).

Число

называется пределом функции

в точке

(при стремлении

к

точке ), если для любого числа

0 найдется такое число

, что для всех значений

и таких, что

,

выполняется неравенство

.

Обозначения:

,

.

Из определения следует, что

, т.е.

.

Неравенства

равносильны условию:

, где

проколотая

- окрестность точки

; неравенство

равносильно условию:

, где

- окрестность точки

. Поэтому определение предела

функции можно записать в символической форме:

.

Замечание 1. Число , вообще говоря, зависит от числа

:

.

Замечание 2. Смысл определения заключается в том, что значения функции

должны

быть сколь угодно «близки» к своему пределу

, как только переменная

достаточно

«близка» к своему пределу

(но не совпадает с ним:

).

Замечание 3. Переменная

может быть обозначена любым другим символом

значение

предела от этого не зависит:

.

Определение 2 (по Гейне или на языке последовательностей).

Число

называется пределом функции

в точке

(при стремлении

к

точке ), если для любой последовательности

,

, сходящейся к числу

,

соответствующая последовательность значений функции

сходится к числу .

В символической форме это определение можно записать так:

.

Равносильность этих двух определений показана в .

Замечание 4. Существование предела функции

при

и само значение этого

предела никак не зависят от значения

, это значение может быть и не определено

. На существование и значение предела функции влияет лишь поведение

функции в проколотой окрестности точки

, т.е. влияют лишь значения

, где

.

Рассмотрим некоторые примеры.

Пример 1.

. Докажем это.

надо доказать, что

.

имеем:

. Пусть

; тогда

:

. Это и означает, что

.

Пример 2.

. Докажем это.

надо доказать, что

.

имеем:

. Пусть

; тогда

:

.

Это и означает, что

.

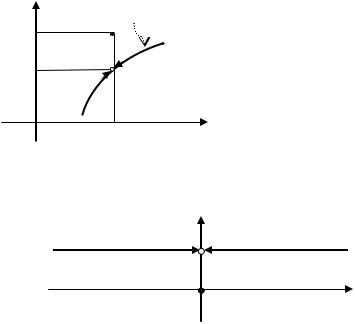
Значение предела функции в точке иногда можно найти графическим методом.

Например, на следующем графике функции видно, что

и

.

если

.

График функции:

если

значениями

(слева от точки ), то получим определение предела слева.

Односторонние пределы можно определить как на языке

- , так и на языке

последовательностей. Дадим определение на языке

- .

Определение 3.

Число называется пределом функции

в точке

справа,

если для любого числа

0 найдется такое число

, что для всех значений

и

таких, что

, выполняется неравенство

.

Обозначения:

,

,

.

93

Определение 4.

Число называется пределом функции

в точке

слева,

если для любого числа

0 найдется такое число

, что для всех значений

и

таких, что

, выполняется неравенство

.

Обозначения:

,

,

.

.

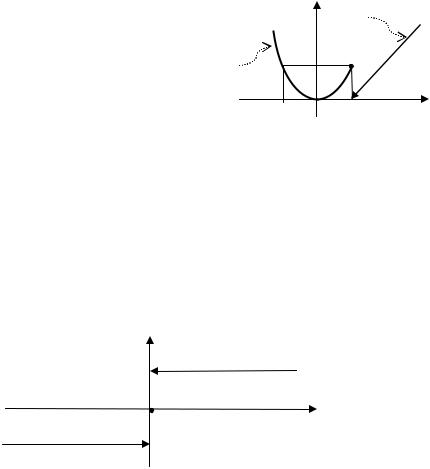
Пример 4.

.

График функции:

Рассмотрим поведение функции при

.

Из графика можно определить односторонние пределы при

:

,

.

Так как

, то

не существует.

Пример 5.

. График функции:

Рассмотрим поведение функции при

. Из графика видно,

что

,

;

, поэтому

не существует.

Предел функции на .

Если область определения

содержит сколь угодно большие положительные

значения , то говорят, что

является точкой сгущения для

; если

содержит сколь

угодно большие отрицательные значения , то говорят, что

является точкой сгущения

для ; если

содержит сколь угодно большие по абсолютной величине значения

, то

говорят, что

является точкой сгущения для .

94

Определение 5. Пусть

является точкой сгущения для

. Число

называется

пределом функции

при

, если для любого числа

0 найдется такое

число

, что для всех

значений

и таких, что

, выполняется неравенство

.

Обозначения:

,

.

Определение 6. Пусть

является точкой сгущения для

. Число

называется

пределом функции

при

, если для любого числа

0 найдется такое

число

, что для всех

значений

и таких, что

, выполняется неравенство

.

Обозначения:

,

.

Определение 7. Пусть

является точкой сгущения для

. Число

называется

пределом функции

при

, если для любого числа

0 найдется такое

число

, что для всех

значений

и таких, что

, выполняется неравенство

.

Обозначения:

,

.

Аналогичные определения можно было бы дать и на языке последовательностей.

Рассмотрим некоторые примеры.

Пример 6.

. Докажем это.

имеем:

.

Возьмем

; тогда

:

.

Это и означает, что

.

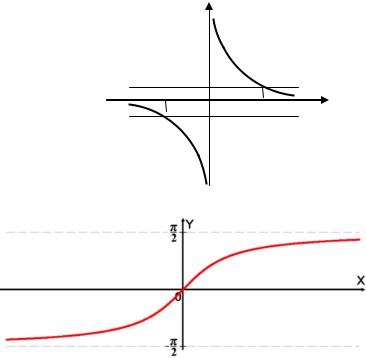
Этот результат можно увидеть и по графику функции: кривая графика лежит внутри

горизонтальной полосы

при

при

и при

.

Пример 7.

,

.

95

Докажем, например, первое равенство.

имеем:

.

Возьмем

; тогда :

.

Это означает, что

. Аналогично доказывается и второе равенство.

Пример 8.

,

.

Докажем, например, второе равенство.

имеем:

.

Возьмем

;

, т.к.

при

.

Тогда

:

.

Это означает, что

.

Аналогично доказывается и первое равенство.

Пример 9.

и

не существуют.

Чтобы доказать это, воспользуемся определением предела на языке

последовательностей.

Для

функции

возьмем

последовательность

,

где

;

тогда

,

;

а

последовательность

предела, как известно, не имеет.

Аналогично и для функции

.

Пример 10.

и

не существуют.

Для доказательства возьмем для функции

последовательность

, где

;

тогда

, а последовательность

расходится. Следовательно,

не существует.

3. Если

, то все значения

будут больше по абсолютной величине

некоторого положительного числа в некоторой проколотой окрестности

:

.

4 (об ограниченности). Функция, имеющая предел

ограничена в некоторой

проколотой окрестности

:

.

При

и

запись свойств 2 4 также следует уточнить, как это

сделано для свойства 1.

5 (предельный переход в неравенстве).

Заданы функции

и

. Пусть

,

при

и выполнено

неравенство:

для всех значений

из некоторой проколотой окрестности

. Тогда

.

6 (о сжатой функции).

Заданы три функции

,

,

и выполнены неравенства:

для всех значений

из некоторой проколотой окрестности

.

Пусть существуют

,

и

.

Тогда существует и

, причем

.

Справедливо следующее утверждение.

Теорема (о замене переменной или о пределе сложной функции).

Пусть существуют пределы:

и

, причем

. Тогда существует

и

.

Доказательство.

Воспользуемся определением предела на языке последовательностей. Для

и

.

Сложная функция

определена в некоторой проколотой окрестности

.

Возьмем

;

тогда

. Получаем:

.

Это означает, что

.

Теорема доказана.

Теорема верна также и в случае односторонних пределов и пределов на .

Пример.

см Пример §

.

см Пример

Замечание.

Без требования:

утверждение теоремы было бы неверным.

Следствие.

Пусть существуют пределы:

и

. Тогда

существует

.

Доказательство.

Так как

и

, то здесь повторяется

доказательство теоремы с тем лишь отличием, что не надо требовать выполнения

условия:

.

при

называется функция

, предел которой при

равен нулю:

.

Символически это можно записать так:

б.м.в. при

;

б.м.в. при

;

б.м.в. при

;

б.м.в. при

;

б.м.в. при

;

б.м.в. при

.

Например:

б.м.в. при

;

б.м.в. при

.

Определение 2.

Функция

называется бесконечно малой величиной (б.м.в.) при

, если для любой последовательности

,

, сходящейся к

числу

, соответствующая

последовательность

значений

функции

стремится к 0:

.

Функция

называется бесконечно малой величиной (б.м.в.) при

, если

для любой последовательности

,

, соответствующая

последовательность значений функции

стремится к 0:

б.м.в. при

;

б.м.в. при

;

б.м.в. при

.

99

Пример.

, где

б.м.в. при

.

Докажем это на языке -

. По определению:

б.м.в. при

. Для

возьмем

; тогда:

, что и требовалось доказать.

Например, функции:

,

,

,

б.м.в. при

.

Замечание.

Из определения б.м.в. следует:

б.м.в.

б.м.в.

б.м.в.

Дана функция

,

. Введем функцию

. Тогда

б. м. в. при

б. м. в. при

.

Таким образом, справедливо следующее утверждение.

Теорема 1.

б. м. в. при

, или:

, где

б. м. в. при

.

Например:

б.м.в. при

, т.к.

.

Аналогичные утверждения верны при

и при

.

Теорема 2.

б. м. в. при

, или:

, где

б. м. в. при

.

Теорема 3.

б. м. в. при

, или:

, где

б. м. в. при

.

,

… ,

б. м. в. при

…

б. м. в. при

ограниченная функция,

б. м. в. при

б. м. в. при

есть бесконечно малая функция:

,

б. м. в. при

б. м. в. при

Аналогичные утверждения верны при

и при

.

Эти свойства и следствия вытекают из аналогичных свойств и следствий для

последовательностей (см. §4 главы 3) и равносильности 2-х определений предела

функции (на языке - и на языке последовательностей).

Примеры.

1.

, т.к.

б.м.в. при

(сумма 2-х б.м.в. при

).

2.

, т.к.

б.м.в. при

(произведение б.м.в.

на

функцию, имеющую предел при

).

3.

, т.к.

б.м.в. при

(произведение б.м.в. при

на ограниченную функцию).

4.

,

,

. Здесь аналогично Примеру 3.

определения пределов на языке

- и на языке последовательностей равносильны.

Теорема. (Правила вычисления пределов функций).

Заданы функции

,

и

. Пусть

,

при

.

Тогда сумма, разность и произведение, а при

и частное функций

и

имеют

предел. При этом выполнены равенства:

2.

;

3.

;