
131
Это утверждение следует из свойства пределов (см. свойство 2 из §2 главы 4).
О непрерывности сложной функции.
Теорема 4. Если функция |
непрерывна в точке |
, а функция |
непрерывна в точке |
|||||||
|
, то сложная функция |
непрерывна в точке . |
|
|
|
|||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
Из непрерывности функции |
в точке |
имеем: |
|
0 |
|
: |
, |
||
|
|
. |
|
|
|
|
|
|
|
|
|
Из непрерывности функции |
в точке |
имеем: |
|
|
0 |
: |
, |
||
|
|
. |
|
|
|
|
|
|
|
|
|
Так как |
, то |
|
|
|
|
. |
Итак, |
0 |
: |
|
, |
|
|
, |
где |
|
область определения |
|||
сложной функции |
. Это и означает непрерывность сложной функции. |
|
||||||||
Замечание.
Вместо доказательства можно было бы просто сослаться на Теорему о пределе сложной функции и Следствие из нее (см. §2 главы 4).
§4. Свойства функций, непрерывных на отрезке.
Вэтом параграфе рассматриваются функции, непрерывные на некотором отрезке
. Это означает, как отмечено выше, непрерывность функций в каждой внутренней
точке этого промежутка, а на концах промежутка соответственно непрерывность справа (в точке ) и слева (в точке ).
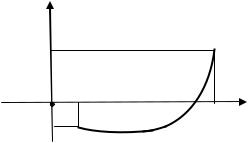
Первая теорема Больцано-Коши (об обращении функции в нуль).
Теорема 1. |
|
|
|
Пусть функция |
определена и непрерывна на отрезке |
. Если функция на |
|
концах промежутка принимает значения разных знаков, то найдется точка внутри |
|||
промежутка, в которой функция обращается в нуль: |
|
|
|
|
: |
. |
|
Теорема имеет следующий геометрический смысл:
если непрерывная кривая переходит с одной стороны оси на другую, то она где-нибудь пересекает эту ось (см. рис.)
Доказательство.
132
Применим метод последовательного деления промежутка. Пусть для определенности
|
|
, а |
. Разделим промежуток |
|
пополам точкой |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
Если окажется, что |
|
|
|
|
|
, то точка |
|
найдена. Пусть |
|
|
|
|
|
|
|
; тогда |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
или |
|
|
|
. В первом случае функция |
|
принимает значения разных |
|
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
знаков на концах промежутка |
|
|
|
, во втором случае |
на концах промежутка |
|
|
. |
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
Выберем тот промежуток, на концах которого функция принимает значения разных |
|||||||||||||||||||||||||||||
знаков, и обозначим его через |
|
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
, |
, |
|
|
и |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Далее повторяем эту процедуру для промежутка |
|
|
. Если |
|
|
|
|
|
|
|
, то |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
получаем промежуток |
- такой, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
, |
|
|
|
, |
|
и |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Если окажется, что |
|
|
|
|
, то точка |
|
|
найдена. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Продолжая этот процесс деления промежутка, мы либо наткнемся на точку, в которой функция обращается в нуль - и доказательство теоремы завершится - либо получим бесконечную последовательность вложенных один в другой промежутков. В последнем случае будем иметь:
|
, |
, |
и |
|
при |
. |
|
|
|
|
|||||
|
Согласно Лемме о вложенных промежутках (см. §9 главы 3) все эти промежутки |
|
|||||
имеют единственную общую точку , причем |
|
. Докажем, что эта точка |
|||||
искомая. |
|
|
|
|
|
|
|
|
Перейдем к пределам при |
в неравенствах: |
, |
|
. |
||
Тогда получим: |
, |
|
. |
|
|
|
|
|
Используя непрерывность функции |
в точке : |
|
|
|
|
|
и |
|
получим: |
и |
, но это возможно лишь, |
|||
если |
. Теорема доказана. |
|
|
|
|
|
|
Доказанная теорема может применяться при решении уравнений: во-первых, для установления факта существования корня; во-вторых, для приближенного вычисления этого корня.
Пример 1. Рассмотрим алгебраическое уравнение нечетной степени:
|
|
. |
Пусть |
|
многочлен нечетной степени. |
Известно (см. §6 главы 4), что |
и |
. Так как многочлен |
является непрерывной функцией и меняет знак на некотором промежутке, то согласно доказанной теореме в какой-то промежуточной точке многочлен обращается в 0.
Следовательно: любое алгебраическое уравнение нечетной степени имеет, по крайней мере один вещественный (действительный) корень.
|
|
|
|
|
|
133 |
Пример 2 (из |
). Найдем корень уравнения |
с точностью до 0,01. |
||||
Пусть |
|
. Вычисляя значения функции |
в целочисленных |
|||
точках, мы увидим, что |
|
, |
Следовательно, непрерывная |
|||
функция |
на концах промежутка |
принимает значения разных знаков. Согласно |
||||
доказанной теореме на интервале |
найдется точка, в которой функция обращается в |
|||||
нуль, т.е. корень уравнения лежит внутри отрезка |
. |
|
|
|||
Разделим отрезок |
на 10 равных частей и вычислим значения |
в точках |
||||
деления: |
|
…; |
|
|
…; |
. |
Так как |
|
, то корень находится внутри отрезка |
. |
|
||
Разделим теперь этот отрезок на 10 равных частей и вычислив значения |
в |
|||||
точках деления, получим: |
|
…; |
|
Это значит, что корень |
||
лежит внутри промежутка |
|
. |
|
|
|
|
Таким образом, с точностью до 0,01 корень данного уравнения равен |
. |
|||||
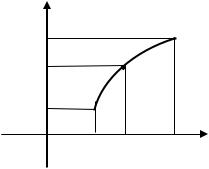
Вторая теорема Больцано-Коши (о промежуточном значении функции).
Теорема 2. |
|
|
|
|
|
Пусть функция |
определена и непрерывна на отрезке |
|
. Если функция на |
||
концах промежутка принимает неравные значения: |
|
, то она принимает и |
|||
любое промежуточное значение между |
и |
: |
|
|
|
, |
или |
|
|
: |
. |
Доказательство. |
|
|
|
|
|
|
|
Возьмем любе число |
, лежащее между |
и |
, и введем новую функцию: |
|
|||
|
|
|
|
. |
|
|
|
Функция |
на концах промежутка принимает значения разных знаков, |
|
|||||
действительно: |
|
|
|
, так как либо |
|
|
|
|
и |
, либо |
и |
. Кроме того, функция |
непрерывна |
||
на |
как разность двух непрерывных функций. |
|
|
|
|||
По первой теореме Больцано-Коши найдется точка внутри промежутка, в которой |
|
||||||
функция |
обращается в нуль, т.е. |
: |
, а это означает, что |
. |
|||
Теорема доказана. |
|
|
|
|
|
|
|
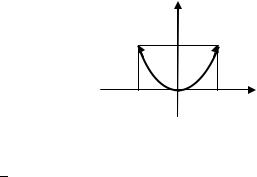
Первая теорема Вейерштрасса (об ограниченности функции).
Теорема 3.
|
|
|
|
|
|
|
134 |
Если функция |
|
определена и непрерывна на отрезке |
, то она ограничена |
||||
на этом отрезке, т.е. |
|
|
|
|
. |
|
|
Доказательство. |
|
|
|
|
|
|
|
Предположим, что функция |
не ограничена на |
. В таком случае для |
|||||
каждого натурального числа |
найдется в промежутке |
такое значение |
, что |
||||
. Тем самым получаем ограниченную последовательность чисел |
|
||||||
|
, для которой |
при |
. |
|
|
||
По Лемме Больцано-Вейерштрасса (см. §11 главы 3) из последовательности |
|||||||
можно выбрать сходящуюся подпоследовательность |
: |
при |
. |
||||
Так как |
|
|
, то |
, т.е. |
|
Следовательно, |
|
определено значение |
. |
|
|
|
|
|
|
Из непрерывности функции |
в точке имеем: |
|
при |
, |
|||
т.е. подпоследовательность |
|
стремится к конечному пределу и значит, она |
|||||
ограничена. Но, с другой стороны: |
при |
и значит, она не ограничена. |
|||||
Полученное противоречие показывает, что предположение о неограниченности функции неверно. Теорема доказана.
Вторая теорема Вейерштрасса (о наибольшем и наименьшем значении функции). |
|
|||||||||||||||||
Теорема 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Если функция |
|
определена и непрерывна на отрезке |
, то она достигает в |
|||||||||||||
этом промежутке своего наибольшего и своего наименьшего значений: |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
. |
|
|
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
По первой теореме Вейерштрасса множество значений функции |
ограничено. |
|||||||||||||||
Следовательно, у этого множества существует |
и |
(см. §10 главы 1). |
Введем |
|
||||||||||||||
обозначения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
, |
|
|
|
. |
|
|
|
|
|
|
|
Надо доказать, что |
|
|
и |
достигаются, т.е. |
|
|
и |
|
||||||||
|
|
|
|
. Докажем первое утверждение. |
|
|
|
|
|
|||||||||
|
|
Предположим, что это не так, т.е. |
выполнено неравенство: |
. |
||||||||||||||
Рассмотрим функцию |
|
|
|
|
|
|
. Функция |
|
определена и непрерывна на |
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||
как отношение двух непрерывных функций с не обращающимся в нуль знаменателем. |
|
|||||||||||||||||
Кроме того, эта функция положительна. По первой теореме Вейерштрасса функция |
|
|||||||||||||||||
ограничена, т.е. |
: |
|
|
|
|
выполнено неравенство: |
. |
Тогда получим: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. Это означает, что число |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
является верхней границей множества |
|
, причем |
|
|
. |
|
|||||||||
|
|
|
|
|
|
|||||||||||||
Но это противоречит тому, что |
- наименьшая верхняя граница |
|
. Полученное |
|||||||||||||||
противоречие доказывает, что не может выполняться неравенство |
|
|
|
|
. |
|||||||||||||
Следовательно, |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||
135
Аналогично доказывается второе утверждение относительно наименьшего значения функции. Теорема доказана.
Следствие. |
|
|
Если область определения |
непрерывной функции |
есть некоторый |
промежуток, то область значений |
также представляет собой некоторый промежуток. |
|
Доказательство. |
|
|
Понятие промежутка было введено в §8 главы 1; промежутки бывают открытыми, полуоткрытыми, замкнутыми, ограниченными и неограниченными. Например, отрезок
это ограниченный замкнутый промежуток, а интервал это ограниченный открытый |
|
||||||
промежуток. |
|
|
|
|
|
|
|
Рассмотрим случай, когда |
|
представляет собой отрезок. Докажем, что тогда |
|
||||
также является отрезком. |
|
|
|
|
|
|
|
Пусть |
непрерывная функция в области определения |
. По |
|
||||
теоремам Вейерштрасса |
|
|
|
, причем |
|
||
|
и |
|
|
|
. |
|
|
Если |
, то по теоремам Больцано-Коши функция |
принимает все |
|||||
промежуточные значения между |
и |
. Это означает, что область значений |
|
||||
функции |
представляет собой отрезок: |
. |
|
|
|||
Если |
, т.е. |
|
, то наименьшее значение функции совпадает с его |
||||
наибольшим значением; тогда |
|
|
постоянная функция. В этом случае |
|
|||
|
отрезок, |
вырожденный в точку . |
|
|
|||
Таким образом, доказано, что если |
отрезок, то и также отрезок. Другими |
||||||
словами: |
|
непрерывный образ отрезка есть отрезок . |
|
||||
Аналогично доказывается утверждение и для других видов промежутков. |
|
||||||
Замечание 1. Для промежутков, отличных от отрезков, уже нельзя утверждать, что |
и |
||||||
всегда будут промежутками одного вида. Например, если |
интервал, то |
не |
|||||
обязательно будет интервалом. |
|
|
|
|
|
||
В качестве примера рассмотрим функцию, |
|
|
|
||||
полученную сужением функции |
|
|
|
|
|
||
на интервал |
. |
|
|
|
|
|
|
Здесь |
, а |
|
. |
|
|
|
|
Замечание 2. Для разрывных функций утверждение Следствия уже не имеет место.
Например, для функции |
(см. Пример 1 из §2) имеем: |
промежуток, а |
не является промежутком. |
|
|
|
|
|
|
136 |
|
§ 5. |
Монотонность и непрерывность функций. |
|
|||
Рассмотрим функцию |
с областью определения . |
|
||||
Теорема 1. |
Если |
промежуток и |
монотонна на , то функция |
либо |
||
непрерывна на , либо имеет лишь точки разрыва 1 рода. |
|
|||||
Доказательство. |
|
|
|
|
|
|
Пусть для определенности функция |
возрастает на и |
произвольная |
||||
внутренняя точка промежутка . Тогда при |
выполняется неравенство: |
|||||
|
, а при |
|
неравенство: |
, т.е. функция ограничена сверху |
||
при |
и ограничена снизу при |
|
. Согласно теоремам |
из §11 |
||
главы 4 существуют конечные пределы: |
|
|
|
|||
|
|
|
и |
|
, |
|
при этом выполняются неравенства: |
|
|
|
|||
|
|
|
(предельный переход в неравенстве, см. §2 главы 4). |
|||
Если |
|
|
, то |
точка непрерывности функции |
; если |
|
|
|
, то |
точка разрыва 1 рода. |
|
||
Для случая, когда |
левый конец промежутка, имеем: |
, а когда |
||||
правый конец промежутка, имеем: |
|
. В этих случаях имеем либо |
||||
одностороннюю непрерывность в точке , либо также разрыв 1 рода. Теорема доказана.
Критерий непрерывности монотонной функции. |
|
|
|
||
Теорема 2. Пусть |
монотонная функция на области определения , где |
||||
промежуток. Тогда для непрерывности функции |
на |
необходимо и достаточно, |
|||
чтобы область значений |
была также промежутком. |
|
|
||
Доказательство. |
|
|
|
|
|
1) Необходимость. Если |
непрерывная функция на |
, где |
промежуток, то |
||
согласно Следствию из §4 область значений |
также представляет собой некоторый |
||||
промежуток. |
|
|
|
|
|
2) Достаточность. Пусть область значений |
промежуток; это означает, что какое бы |
||||
число ни взять между граничными значениями этого промежутка, всегда найдется
такое значение |
, в котором |
. Возьмем произвольную точку и |
|||
докажем, что |
точка непрерывности функции |
. |
|
||
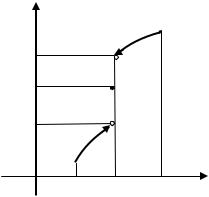
Предположим, что |
точка разрыва функции |
и |
внутренняя точка |
||
промежутка . Согласно Теореме 1 эта точка может быть только точкой разрыва 1 рода,
т.е. существуют конечные пределы |
, |
и |
|
. Само |
значение функции в этой точке лежит между этими пределами: |
|
|
||
|
, если |
возрастающая функция или |
|
|
|
, если |
убывающая функция. |
|
|
Тогда какое бы ни взять число |
между |
и |
, |
, не |
существует ни одного значения , в котором |
. |
|
|
|
137
Другими словами, множество
не может быть промежутком, так как
весь интервал между |
и |
кроме значения |
не входит в это множество. |
В случае, когда |
граничная точка |
промежутка , рассуждения будут аналогичными. Теорема доказана.
Непрерывность обратной функции. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Рассмотрим строго монотонную функцию |
с областью определения |
и |
|||||||||||||||||
областью значений . Для нее существует обратная функция |
(см. §6 главы 2) с |
|||||||||||||||||||
областью определения |
и областью значений . |
|
|
|
|
|
|
|
||||||||||||
Лемма. Если функция |
|
строго возрастающая, то и обратная функция |
|
также |
||||||||||||||||
строго возрастающая; если функция |
|
|
|
строго убывающая, то и обратная функция |
||||||||||||||||
|
также строго убывающая. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Доказательство. |
Пусть |
|
строго возрастающая функция на |
; тогда |
, |
|
||||||||||||||
|
|
|
. |
Возьмем произвольные значения |
, |
, |
; докажем, |
|||||||||||||
что |
|
|
. Предположим, что это не так, т.е. |
|
|
. |
|
|||||||||||||
Если |
|
|
, то |
|
|
|
|
|
|
|
|
|
|
, что невозможно. |
|
|||||
Если |
|
|
, то |
|
|
|
|
|
|
|
|
|
|
, что также невозможно. |
||||||
|
Аналогично для случая строго убывающей функции |
. Лемма доказана. |
|
|||||||||||||||||
Теорема 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
|
строго монотонная функция на |
, где |
некоторый промежуток. |
|||||||||||||||
Тогда если |
|
непрерывна на , то обратная функция |
|
непрерывна на . |
||||||||||||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Так как |
|
непрерывна на промежутке |
, то по Теореме 2 множество |
|
|||||||||||||||
является промежутком. По Лемме функция |
|
|
|
является строго монотонной функцией. |
||||||||||||||||
Таким образом, имеем строго монотонную функцию |
|
|
, заданную на промежутке |
|||||||||||||||||
и принимающую значения в промежутке |
. Следовательно, по Теореме 2 функция |
|
||||||||||||||||||
|
непрерывна на |
. |
Теорема доказана. |
|
|
|
|
|
|
|
||||||||||
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
непрерывна на промежутке |
|
|
|
|
|
|
|
непрерывна на |
|
. |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||
2) |
|
|
непрерывна на промежутке |
|
|
|
|
|
|
|
||||||||||
|
непрерывна на |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
непрерывна на промежутке |
|
|
|
|
|
|
|
|
|
|
непрерывна на |
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
4) |
непрерывна на промежутке |
|
|
|
|
|
|
|
|
|
непрерывна на |
|
. |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
138
§ 6. Понятие равномерной непрерывности.
Рассмотрим функцию |
с областью определения . Пусть |
промежуток, |
инепрерывна на . Это означает, что функция непрерывна в каждой
точке |
. |
|
|
|
|
По определению (на языке - |
) непрерывность функции в точке означает: |
||||
|
|
0 |
: |
, |
. |
Непрерывность функции на всем промежутке |
можно сформулировать |
||||
следующим образом: |
|
|
|
||
|
, |
0 |
: |
, |
. |
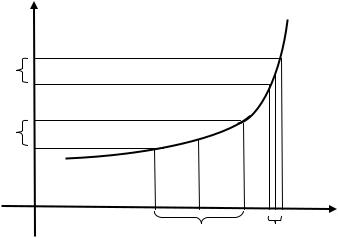
Из этого определения видно, что число может зависеть не только от , но и от . Ниже на рисунке видно, что число , пригодное на участке, где функция изменяется медленно (график представляет пологую кривую), уже не годится на участке быстрого изменения функции (где график круто поднимается или опускается).
|
Возникает вопрос: для функции |
, непрерывной в промежутке , существует |
||||||||
ли, при заданном |
, такое |
, которое годилось бы для всех точек из промежутка |
? |
|||||||
|
Если ответ на этот вопрос утвердительный, то функция называется равномерно |
|||||||||
непрерывной на промежутке . |
|
|
|
|
|
|
||||
Определение 1. Функция |
называется равномерно непрерывной на промежутке |
, |
||||||||
если |
|
0 |
: |
|
, |
|
|
. |
|
|
|
Сформулируем равносильное определение. |
|
|
|
|
|||||
Определение 2. Функция |
называется равномерно непрерывной на промежутке |
, |
||||||||
если |
|
0 |
: |
|
, |
|
|
. |
|
|
|
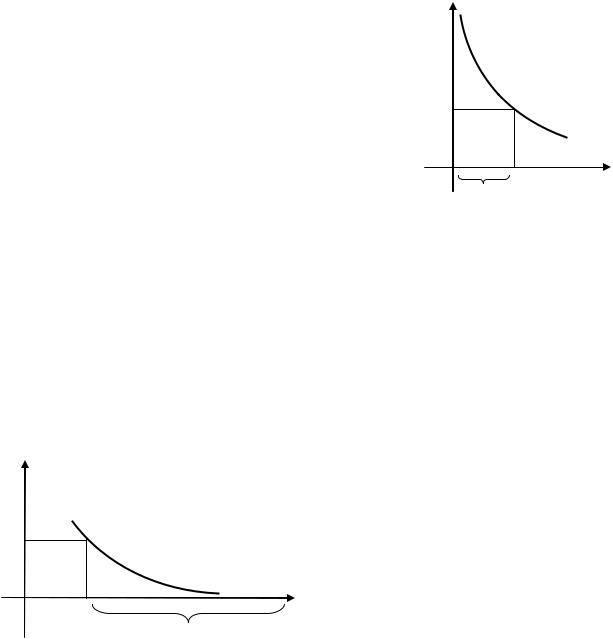
В определении говорится о любых двух точках |
и из промежутка |
, отстоящих |
|||||||
друг от друга на расстоянии, меньшем, чем |
; при этом |
зависит только от |
(и не зависит |
|||||||
от того, в какой части промежутка |
лежат точки |
и |
). |
|
|
|||||
139
Любая равномерно непрерывная функция на промежутке является просто непрерывной на данном промежутке, но обратное утверждение неверно. Функция может быть непрерывной на промежутке, но не быть равномерно непрерывной на нем.
Одна и та же непрерывная функция может быть равномерно непрерывной на одном промежутке и не быть таковой на другом промежутке.
Примеры.
1) |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
Покажем, что функция |
|
|
|
не является |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
равномерно непрерывной на промежутке . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
Возьмем |
; предположим, что |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Но это невозможно, т.к. можно взять, например: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и при достаточно больших |
будет выполняться |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
, т.к. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Следовательно, наше предположение |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
неверно и функция |
|
|
|
|
|
не является равномерно непрерывной на промежутке . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2) |
|
|
|
|
, |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Покажем, что функция |
|
|
|
является равномерно непрерывной на промежутке . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительно, |
0 возьмем |
; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда |
|
, |
|
|
|
|
|
|
, т.е. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Следовательно, функция |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
является равномерно непрерывной на промежутке . |
||||||||||||||||||||||||||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
. График этой функции приведен в §1 главы 4. |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
Покажем, что функция |
|
|
не является равномерно непрерывной на промежутке . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Возьмем |
|
, |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
; тогда |
|
|
|
|
|
|
, |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
140 |
|
|
Здесь мы видим, что разность |
|
|
|
|
|
|
|
может быть сколь угодно малой, а |
||||||||||||||||||
разность функций по модулю |
|
|
|
|
|
|
|
|
не может быть меньше |
. Это означает, что |
|||||||||||||||||
|
не является равномерно непрерывной на промежутке . |
|
|
||||||||||||||||||||||||
4) |
|
|
, |
|
, где |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Покажем, что функция |
|
|
является равномерно непрерывной на промежутке . |
|||||||||||||||||||||||
Используя неравенство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(см. §5 главы 4), можно записать: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда |
|
|||
|
Для произвольного числа |
0 |
возьмем |
; |
, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Это и означает равномерную непрерывность функция |
|
на промежутке . |
||||||||||||||||||||||||
Приведенные примеры показывают, что свойство равномерной непрерывности функции на промежутке связано как с самой непрерывной функцией, так и с тем промежутком, на котором она рассматривается.
Оказывается, что свойство непрерывности функции на промежутке и свойство равномерной непрерывности на промежутке совпадают в случае, когда промежутком является отрезок, т.е. ограниченный замкнутый промежуток. Это следует из следующей теоремы.
Теорема Кантора.
Если функция непрерывна на отрезке , то она и равномерно непрерывна на этом отрезке.
Доказательство этой теоремы можно найти, например в и .
Понятие равномерной непрерывности играет важную роль в математическом анализе и его приложениях. Некоторые математические утверждения справедливы только при условии, что функция является не просто непрерывной, а равномерно непрерывной на промежутке.
