Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Введение в мат.анализ

.pdf

Скачиваний:

Добавлен:

27.08.2020

Размер:

3.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2316 17 18 19 20 21 22 23 > Следующая >>>

151

Действительно:

	- это уравнение окружности с центром в
начале координат;

		- это
уравнение окружности с центром в точке		.

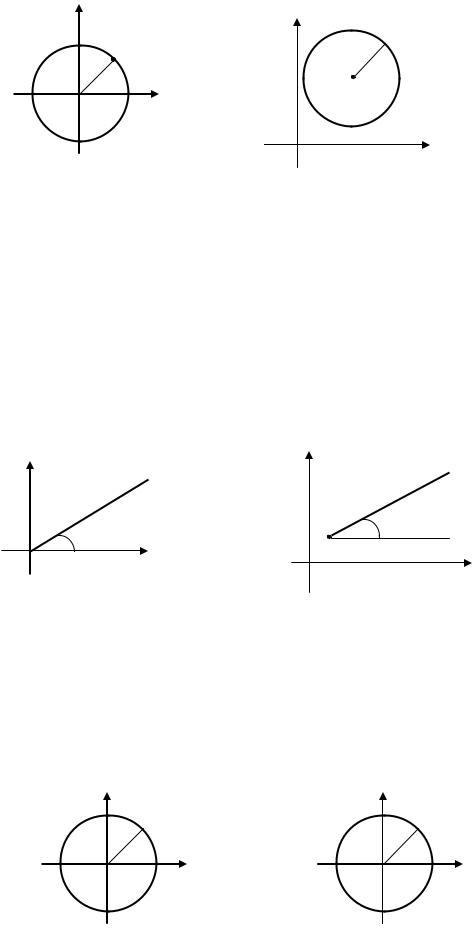
2. Лучи:

- выходящие из начала координат; - выходящие из точки .

Это следует из определения аргумента комплексного числа.

3. Круги радиуса

-открытый круг с центром в начале координат;

-замкнутый круг с центром в начале координат;

- открытый круг с центром в точке ; - замкнутый круг с центром в точке .

152

4. Внешности кругов радиуса

-открытая внешность круга с центром в начале координат;

-замкнутая внешность круга с центром в начале координат;

- открытая внешность круга с центром в точке ; - замкнутая внешность круга с центром в точке .

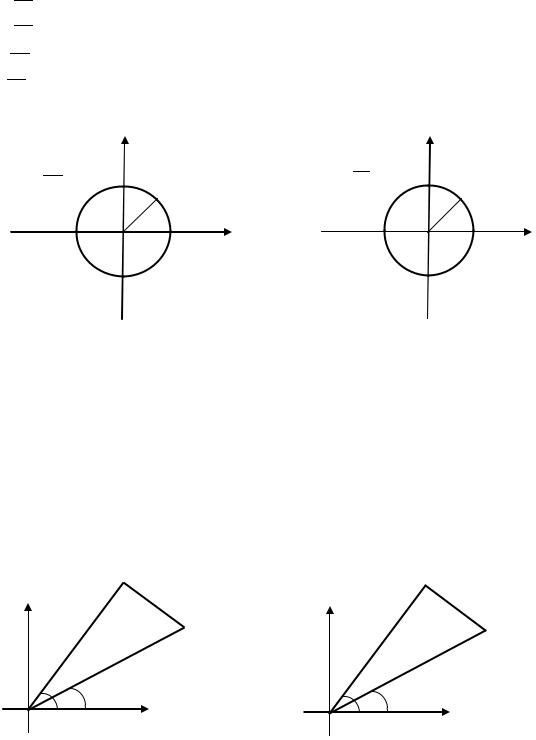
5. Секторы:

-открытый сектор с вершиной в начале координат;

-замкнутый сектор с вершиной в начале координат;

-полуоткрытый сектор с вершиной в начале координат;

- открытый сектор с вершиной в точке	;
- замкнутый сектор с вершиной в точке	;
- полуоткрытый сектор с вершиной в точке ;
- полуоткрытый сектор с вершиной в точке .

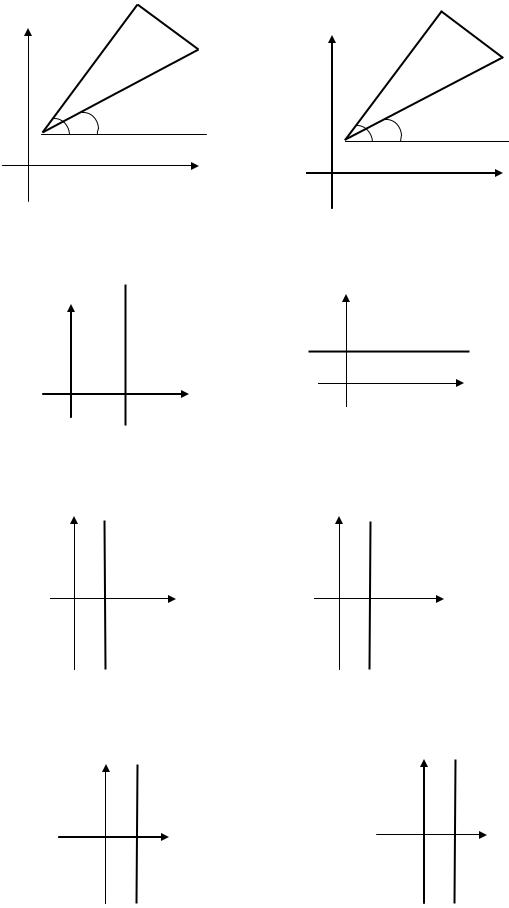
153

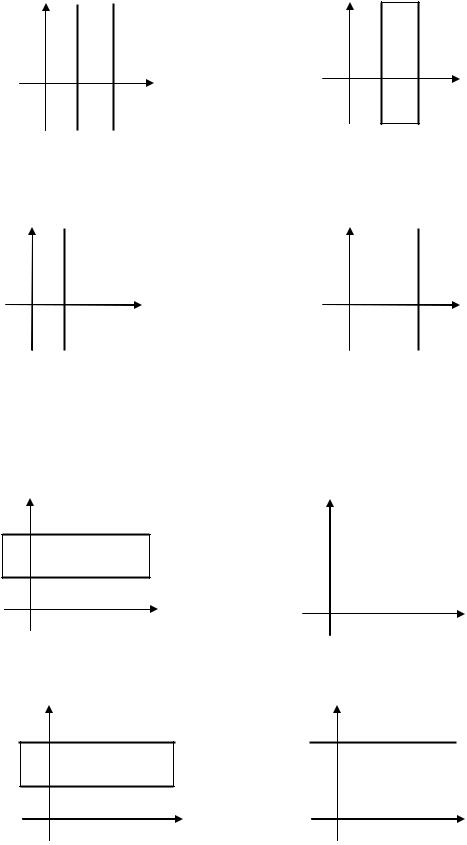
6. Вертикальные и горизонтальные прямые:

- вертикальная прямая.

- горизонтальная прямая.

7. Вертикальные и горизонтальные полуплоскости:

- вертикальная	- вертикальная
открытая правая полуплоскость.	замкнутая правая полуплоскость.

- вертикальная	- вертикальная
открытая левая полуплоскость.	замкнутая левая полуплоскость.

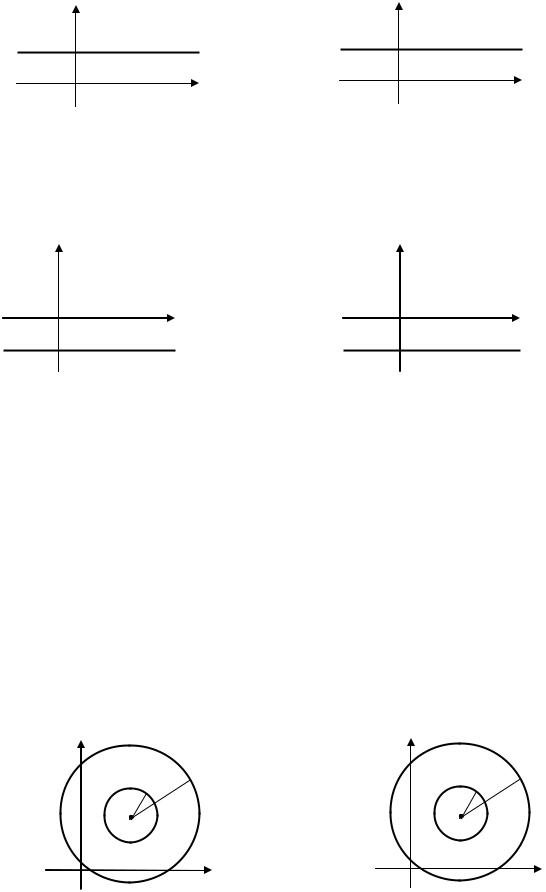
154

- горизонтальная	- горизонтальная
открытая нижняя полуплоскость.	замкнутая нижняя полуплоскость.

- горизонтальная	- горизонтальная
открытая верхняя полуплоскость.	замкнутая верхняя полуплоскость.

8. Круговые кольца	:
	- открытое круговое кольцо с центром в точке ;
	- замкнутое круговое кольцо с центром в точке .
	- полуоткрытое круговое кольцо с центром в точке ;
	- полуоткрытое круговое кольцо с центром в точке .

155

9. Вертикальные полосы			:

-			-
вертикальная открытая полоса.			вертикальная замкнутая полоса.

-	-
вертикальная полуоткрытая полоса.	вертикальная полуоткрытая полоса.
10. Горизонтальные полосы	:

-	-
горизонтальная открытая полоса.	горизонтальная замкнутая полоса.

-	-
горизонтальная полуоткрытая полоса.	горизонтальная полуоткрытая полоса.

156

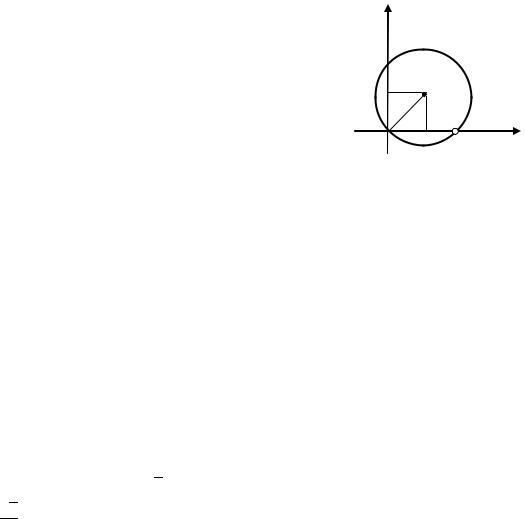
Пример 1.
	Изобразить на комплексной плоскости множество		.
	Изобразить на комплексной плоскости множество		.
Решение.
	Пусть	, тогда

;

Первое уравнение задает окружность с центром в точке

и радиуса

;

второе условие исключает точку

, лежащую на этой окружности. Изобразим

полученное множество на комплексной плоскости.

Ответ.

Окружность с центром в точке

и радиуса

, из которой удалена

точка

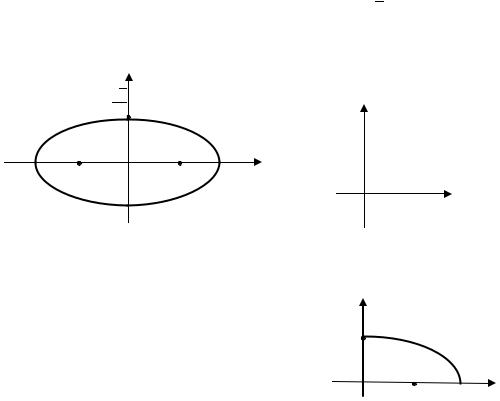
Пример 2.
Изобразить на комплексной плоскости множество
Решение.			.
			.

Множество	представляет собой пересечение двух множеств:			, где
	,	.
Множество	задается условием:		. Геометрически это
неравенство означает, что сумма расстояний от точки		до точек 1 и -1 не превосходит 4.

Как известно, множество точек на плоскости, для которых сумма расстояний до двух заданных точек есть величина постоянная, представляет собой эллипс с фокусами в заданных точках и большой осью, равной этой сумме.

Поэтому множество - это внутренняя часть эллипса, включая его границу. Фокусы этого эллипса находятся в точках 1 и -1 на вещественной оси, его большая ось равна , а малая ось равна ; соответственно большая полуось равна , а малая полуось

равна .

157

Множество задается неравенствами: . Это множество

представляет собой сектор, ограниченный осями координат и совпадающий с первой четвертью.

Множество	является общей частью множеств	и , т.е. совпадает с той частью
эллипса, которая лежит в первой четверти.
Ответ.
Первая четверть эллипса с каноническим

уравнением	.

§ 4.

Тригонометрическая форма комплексного числа.

Пусть

- комплексное число, не равное нулю,

- его модуль и

- его аргумент.

Из формул:

получаем:

Запись вида:

- называется тригонометрической

формой комплексного числа

, при этом

Например:

;

Для комплексно-сопряженных чисел и

тригонометрическая форма имеет вид:

Пусть

Равенство двух комплексных чисел, заданных в тригонометрической форме, определяется следующими условиями:

158

При выполнении арифметических операций (сложения, вычитания, умножения и деления) над комплексными числами можно пользоваться и алгебраической и тригонометрической формой их записи.

Алгебраическая форма записи удобна при сложении и вычитании комплексных чисел, а тригонометрическая форма особенно удобна при умножении и делении комплексных чисел (а также при возведении в степень и извлечении корня). Покажем это.

Умножение и деление комплексных чисел в тригонометрической форме.

Пусть	,	.
Найдем их произведение.

Итак,

, где

Таким образом, получаем следующее правило.

При умножении комплексных чисел их модули перемножаются, а аргументы складываются:

			,
(здесь вместо		пишем	и равенство понимаем как равенство множеств).
Геометрически это означает,
что произведение		получается поворотом
вектора на угол, равный			, и изменением
модуля вектора	в	раз.

Очевидно, что это правило распространяется на произведение любого конечного числа сомножителей:

Пример 1.

159

Пример 2.

,						,

Пусть

Найдем частное

Итак, , где , .

Таким образом, получаем следующее правило.

При делении комплексных чисел их модули делятся, а аргументы вычитаются:


(здесь вместо		пишем		и равенство понимаем как равенство множеств).
Геометрически это означает,
что частное	получается поворотом


вектора на угол, равный				, и
изменением модуля вектора			в	раз.

Пример 3.

160

§ 5. Возведение комплексного числа в целую степень.

Пусть	натуральное число	. Тогда по определению:		.
				раз
Из формул предыдущего параграфа:
		,
при	получаем:
	,		, т.е.
при возведении комплексного числа в натуральную степень				модуль

комплексного числа возводится в эту степень, а его аргумент увеличивается в				раз.
Формула Муавра.
Пусть	,	; тогда	,
.	Следовательно:			.

Получаем формулу Муавра:

, .

Введем понятие степени с нулевым и с целым отрицательным показателем для комплексных чисел так же, как и для вещественных чисел:

,, .

Покажем, что формула Муавра верна для всех целых значений показателя степени.

Таким образом, имеем:

формула Муавра.

В частности

;

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2316 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в папке Учебники

#
27.08.20203.23 Mб23Введение в мат.анализ.pdf
#
27.08.20203.47 Mб25Линейная алгебра и аналитическая геометрия.pdf