Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Введение в мат.анализ

.pdf

Скачиваний:

Добавлен:

27.08.2020

Размер:

3.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 234 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

используем формулы

что и требовалось доказать.

Следовательно, формула бинома Ньютона верна для всех .

Глава 2. Последовательности и функции.

Содержание

§1. Числовые последовательности…………………………………………….. 33

§2. Арифметическая и геометрическая прогрессии………………….. 34

§3. Простейшие свойства последовательностей……………………….. 36

§4. Понятие функции……………………………………………………………………. 39

§ 5. Основные характеристики функции ………………………………………		43
§ 6.	Обратная функция …….………………………………………………………….	47
§ 7. Основные элементарные функции ………………………………………		49
§ 8.	Классы элементарных функций ………..………………………………….	56

§ 1. Числовые последовательности.

Определение. Пусть каждому натуральному числу

поставлено в соответствие по

некоторому правилу (закону) действительное число .

Тогда говорят, что задана

последовательность чисел или числовая последовательность

Число – первый член последовательности, число

– второй член

последовательности, …, число

– -й член последовательности и т.д.

Числовая последовательность обычно задается формулой ее

- го (общего) члена:

Примеры числовых последовательностей:

– последовательность натуральных чисел,

;

– последовательность квадратов натуральных чисел,

;

– последовательность чисел, обратных к натуральным числам,

;

….} – числовая последовательность, в которой на четном месте

стоит

, а на нечетном месте стоит ,

;

….} – постоянная последовательность,

( – произвольное число).

Если последовательность задана формулой общего члена

то можно

вычислить значение любого члена этой последовательности, подставив в формулу значение номера .

Числовая последовательность может быть задана рекуррентным соотношением, т.е. формулой, выражающей каждый член последовательности через предыдущие члены:

рекуррентное соотношение.

Вэтом случае дополнительно задаются один или несколько первых членов последовательности.

Пример. Последовательность задана рекуррентной формулой:		.
Найти .
Решение.	;	;
	.

Ответ.

Таким образом, если последовательность задана рекуррентным соотношением,

то для вычисления нужно вычислить все предыдущие значения до			.
Интересным примером числовой последовательности, заданной рекуррентным
соотношением, является последовательность чисел Фибоначчи:
,	;	.
Первые члены этой последовательности:
;		;	;
;		;	и т. д.
Получаем последовательность чисел Фибоначчи:			.

Важными примерами числовых последовательностей являются арифметическая и геометрическая прогрессии.

§ 2. Арифметическая и геометрическая прогрессии.

Определение. Арифметической прогрессией называется такая числовая последовательность , для всех членов которой выполняется равенство:

Число называется разностью арифметической прогрессии.

Каждый член арифметической прогрессии получается прибавлением к предыдущему члену одного и того же слагаемого, не зависящего от номера .

Таким образом, арифметическая прогрессия задается рекуррентным соотношением. Арифметическая прогрессия может быть задана и формулой общего

( -го) члена:

Вывод формулы. Докажем формулу общего члена методом математической индукции.

) база индукции;

при

имеем:

верное равенство.

б) индукционный переход;

пусть при

имеем верное равенство:

; надо доказать, что

равенство верно и для

, т.е.

Для этого запишем:

, что и

требовалось доказать.

Арифметическая прогрессия полностью определяется заданием ее первого члена

и разности :

{

;

; ….}.

Примеры арифметическая прогрессий:

(здесь:

;

(здесь:

;

(здесь:

Обозначим через

сумму первых

членов арифметической прогрессии:

…

Например:

и т.д.

Докажем формулу:

Применим метод математической индукции.

) база индукции;

при

имеем:

верное равенство.

б) индукционный переход;

пусть при

имеем верное равенство:

; надо доказать,

что равенство верно и для

, т.е.

Для этого запишем:

. Формула доказана.

Например:

	Определение. Геометрической прогрессией называется такая числовая
последовательность		, для всех членов которой выполняется равенство:
		.
Число	называется знаменателем геометрической прогрессии.
	Каждый член геометрической прогрессии получается умножением предыдущего
члена на один и тот же множитель, не зависящий от номера .
	Таким образом, геометрическая прогрессия задается рекуррентным

соотношением. Геометрическая прогрессия может быть задана и формулой общего ( -го) члена:

Вывод формулы. Докажем формулу общего члена методом математической индукции.

) база индукции;

при

имеем:

верное равенство.

б) индукционный переход;

пусть при

имеем верное равенство:

; надо доказать, что

равенство верно и для

, т.е.

. Для этого запишем:

, что и требовалось доказать.

Геометрическая прогрессия полностью определяется заданием ее первого члена

и знаменателя :

Далее предполагается, что

Если

, то все члены геометрической прогрессии равны между собой:

При

все члены геометрической прогрессии одного знака, а при

знаки

членов геометрической прогрессии чередуются.

Примеры геометрических прогрессий:

(здесь

);

;

(здесь

);

Обозначим через

сумму первых

членов геометрической прогрессии:

…

Например:

и т.д.

Если	, то	.
Пусть	, тогда справедлива следующая формула:

( ).

Вывод формулы. Применим метод математической индукции. ) база индукции;

при

имеем:

верное равенство.

б) индукционный переход;

пусть при

имеем верное равенство:

; надо доказать, что

равенство верно и для

, т.е.

Для этого запишем:

. Формула доказана.

Например:

;

§ 3. Простейшие свойства последовательностей.

Рассмотрим свойства последовательностей: монотонность и ограниченность.

Определение. Числовая последовательность называется возрастающей (строго возрастающей), если каждый ее член не меньше (больше) предыдущего, т.е. для

всех натуральных	верно неравенство:	. Обозначение:	.
Определение. Числовая последовательность		называется убывающей
(строго убывающей), если каждый ее член не больше (меньше) предыдущего, т.е.			для
всех натуральных	верно неравенство:	. Обозначение:	.
Определение. Числовая последовательность		называется монотонной

(строго монотонной), если она является возрастающей (строго возрастающей) или

убывающей (строго убывающей).

Примеры:
-	строго , т.к.	;
-	строго , т.к.	;

-	не является монотонной.

Пример. Определить характер монотонности числовой последовательности

Решение. Сравним значения

и :

;

Ответ.

строго .

Замечание. Понятие монотонности сохраняется, если неравенство

или

выполняется для всех натуральных чисел

, начиная только с какого-то номера, т.е.

где

Арифметическая прогрессия является строго возрастающей при

и строго

убывающей при

. Монотонность геометрической прогрессии определяется

следующими условиями:

;

– не монотонна.

;

– не монотонна.

Определение. Числовая последовательность

называется ограниченной сверху,

если

такое, что

выполняется неравенство:

Определение. Числовая последовательность

называется ограниченной снизу,

если

такое, что

выполняется неравенство:

Определение. Числовая последовательность

называется ограниченной, если

такие, что

выполняются неравенства:

Замечание. Определение ограниченной последовательности равносильно следующему

определению:

ограниченная последовательность

Определение. Числовая последовательность

называется неограниченной,

если она не является ограниченной.

Используя отрицание к понятию

ограниченная последовательность

можно дать

следующее определение неограниченной последовательности:

неограниченная последовательность

Примеры:

1).

ограниченная последовательность, т.к.

;

2).

ограниченная последовательность, т.к.

;

3).

ограниченная последовательность, т.к.

;

4).

ограниченная последовательность, т.к.

;

5).

(здесь:

неограниченная

последовательность.

Действительно: согласно аксиоме Архимеда

натуральное число

;

возьмем

; тогда

6).

, (

фиксированное число) неограниченная последовательность.

Действительно:

составим число

; согласно аксиоме Архимеда

натуральное число

;

тогда

7).

, (

фиксированное число)

неограниченная последовательность.

Действительно:

составим число

; согласно аксиоме

Архимеда

натуральное число

; тогда

Последовательность

Рассмотрим последовательность, имеющую важное значение в теории пределов и

заданную общим членом

Исследуем данную последовательность на монотонность и ограниченность.

Исследование на монотонность.

1-й способ. Этот способ основан на применении неравенства Бернулли (глава 1, § 3):

где

; если

, то неравенство

строгое.

Докажем, что

или равносильное неравенство:

. Для этого

запишем сначала цепочку равенств:

Далее применим неравенство Бернулли для

(заметим, что

Продолжаем цепочку равенств и неравенств:

Получили неравенство:

или

. Следовательно, данная

последовательность строго возрастает:

2-й способ. Этот способ основан на применении формулы бинома Ньютона (глава 1, §11):

Подставляя в эту формулу		, получим:

Заметим, что

представляет собой сумму положительных слагаемых, т.к. каждая

скобка имеет вид:

, причем

При переходе от к

количество положительных слагаемых в сумме увеличится

на 1, а в каждом слагаемом скобки

заменятся на скобки

. Так как

, то каждое слагаемое в

также увеличится по сравнению с .

Следовательно,

, т.е. последовательность строго возрастает:

Исследование на ограниченность.

Выше было показано, что последовательность

ограничена снизу:

Покажем, что она ограничена и сверху.

В разложении

по формуле бинома Ньютона все скобки вида

ограничены:

. Поэтому можно сделать оценку:

Полученное неравенство можно усилить, заменив числа 3, 4, 5, …, стоящие в знаменателях дробей, числом 2:

Сумму в скобке вычислим по формуле суммы членов геометрической прогрессии:

Следовательно:

Таким образом, последовательность

, где

, возрастает и

ограничена:

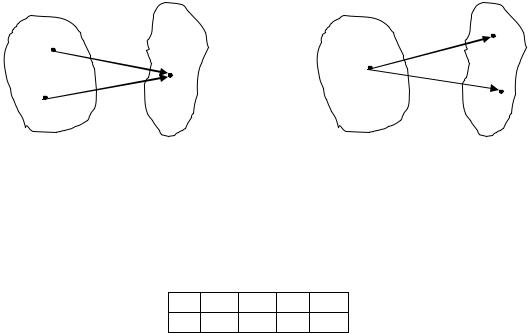
§ 4. Понятие функции.

Определение. Пусть даны числовых множества и . Функцией из	в
называется закон (правило, соответствие), по которому каждому элементу	из
множества соответствует единственный элемент из множества .

Элемент называется независимой переменной (аргументом), а элемент

называется зависимой переменной (функцией).
Обозначения:	.
Например, числовая последовательность	это функция, заданная на
множестве натуральных чисел:		.
Если множества и не заданы, а указано только правило		, по которому
элементу соответствует элемент , то в этом случае считается, что		. Тогда

функцией называется само правило . При этом возникает задача нахождения области определения и области значений функции.

Определение. Областью определения функции						называется множество всех
значений	, при которых	имеет смысл. Обозначения:				,	или .
Областью значений функции			называется множество всех значений					,	которые
может принимать функция		при		.	Обозначения:	,	или .
Замечание. Из определения функции следует, что одному и тому же значению									не могут
соответствовать различные значения			т.е.	если		и	,	то	.
С другой стороны, различным значениям				может соответствовать одно и то же значение
, т.е. если	и	,	то	и	не обязательно совпадают.

) возможно

б) невозможно

Способы задания функции.

1). Табличный способ. Функция задается с помощью таблицы отдельных значений аргумента и соответствующих им значений функции:

…

Например, табличный способ применяется при записи результатов экспериментов, когда никакие формулы заранее неизвестны.

2). Графический способ. Функция задается с помощью графика.

<<< < Предыдущая 1 2 34 / 234 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в папке Учебники

#
27.08.20203.23 Mб23Введение в мат.анализ.pdf
#
27.08.20203.47 Mб25Линейная алгебра и аналитическая геометрия.pdf