Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Введение в мат.анализ

.pdf

Скачиваний:

Добавлен:

27.08.2020

Размер:

3.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2315 16 17 18 19 20 21 22 23 > Следующая >>>

141

Глава 6. Комплексные числа.

Содержание

§ 1.	Определение комплексных чисел ………………………………………………… 142
§ 2.	Геометрическое представление комплексных чисел ……………..……… 148
§ 3.	Основные множества на комплексной плоскости	………………..……… 150
§ 4.	Тригонометрическая форма комплексного числа	………………………… 157

§5. Возведение комплексного числа в целую степень ………………………… 160

§6. Извлечение корня из комплексного числа ……………………………………… 164

§ 7. Предел последовательности комплексных чисел ………………………… 169 § 8. Показательная форма комплексного числа ………………………………… 172

142

§ 1. Определение комплексных чисел.

Комплексное число - это упорядоченная пара вещественных (действительных)

чисел, называемых его компонентами:
, где	.

Для того чтобы полноправно называть эти пары «числами», нужно уметь их складывать и вычитать, умножать и делить. Для этого нужно сформулировать законы (аксиомы) этих действий, а также ввести понятие равенства этих пар.

I. Пары и считаются равными тогда и только тогда, когда равны их соответствующие компоненты:

II. Суммой пар		и	называется пара		, т.е.
				.
III. Произведением пар			и	называется пара	, т.е.
					.
IV. Пара	отождествляется с вещественным (действительным) числом :
				.
В частности:		,		и т.д.

Проверим, не противоречит ли аксиома 4 «обычным» законам действий над вещественными числами.

I.			.
II.			.
III.			.

Как видим, противоречия с «обычными» законами действий над вещественными числами здесь нет.

Из аксиомы IV следует, что вещественные (действительные) числа можно рассматривать как частный случай комплексных чисел (с нулевой второй компонентой).

Следствие 1. Пусть - произвольное вещественное число, тогда справедливо равенство:

Действительно:			.
В частности:	,	,	и т.д.

143

Следствие 2.	.
Действительно:

Легко проверить, что привычные нам свойства действий над вещественными числами сохраняются и при переходе к комплексным числам.

Свойства действий.

1. Коммутативность сложения:

2. Ассоциативность сложения:

3. Свойство нуля при сложении чисел:

4. Существование противоположного числа:

5. Коммутативность умножения:

6. Ассоциативность умножения:

7. Дистрибутивность:

8. Свойство единицы при умножении чисел:

9. Существование обратного числа:
если	, то	- такое, что			.
Действительно, так как			, то			,
Действительно, так как			, то			,
т.е.				.
т.е.				.

144

После введения действий сложения и умножения комплексных чисел можно ввести действия вычитания и деления как обратные к действиям сложения и умножения:

где .

Таким образом, определены все 4 арифметических действия над комплексными числами, причем свойства этих действий аналогичны свойствам действий над вещественными числами.

Множество всех комплексных чисел обозначается буквой :

Так как вещественные числа являются частным случаем комплексных чисел, то

множество всех вещественных чисел			является подмножеством множества всех
комплексных чисел:		.
Если	, то первая компонента комплексного числа			называется вещественной
частью этого числа и обозначается			, а вторая компонента называется его мнимой
частью и обозначается		:
			,	.
Заметим, что и мнимая часть и вещественная часть комплексного числа являются
вещественными числами:		,	.
Замечание.
Множество вещественных чисел			является упорядоченным множеством (так же,
как и множества	, и ), т.е. на этих множествах введены отношения « » (меньше) и
« » (больше).

В отличие от них, множество комплексных чисел не является упорядоченным. Это означает, что комплексные числа не сравнимы между собой, т.е. нельзя сказать, какое из двух комплексных чисел больше или меньше другого.

Мнимая единица.
Комплексное число		называется мнимой единицей.
Мнимая единица обладает уникальным свойством:

			.
Действительно:				.
Следствие 3.
Для любого	справедливы формулы:
;	;	;		.
Действительно:
	;	;		;
		;		.

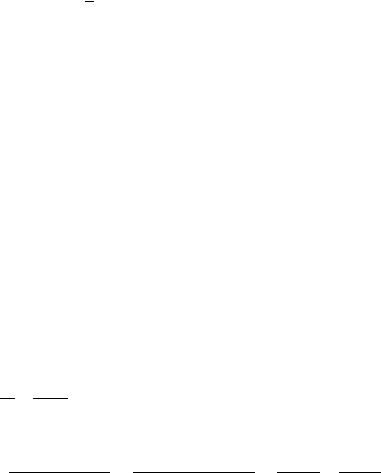
145

Алгебраическая форма комплексного числа.

Пусть

- комплексное число; представим его в следующем виде:

Запись вида:

- называется алгебраической формой комплексного числа

при этом

, т.е.

Например:

;

Комплексные числа вида:

- называются чисто мнимыми числами.

Комплексно-сопряженные числа.

Комплексные числа

- называются

комплексно-сопряженными.

Например:

;

Результатом умножения двух ненулевых комплексно-сопряженных чисел всегда будет вещественное и положительное число (см. Следствие 2):

Действия с комплексными числами в алгебраической форме.

Используя аксиомы , а также свойства арифметических действий , можно выполнять арифметические действия с комплексными числами в алгебраической форме.

Пусть , .

- Сложение и вычитание комплексных чисел.

- Умножение комплексных чисел.

используем формулу

- Деление комплексных чисел.

числитель и знаменатель дроби умножим на число сопряженное знаменател

146

Пример 1.

Выполнить действия:

и записать

результаты в алгебраической форме, если

Решение.

;

Пример 2.

Вычислить

и записать результат в алгебраической форме.

Решение.

Применим формулы сокращенного умножения:

;

Тогда получим:

При действиях с комплексными числами в алгебраической форме может оказаться полезной следующая формула: .

Свойства комплексно-сопряженных чисел.


1.	;		2.	; 3.		; 4.		;
1.	;		2.	; 3.		; 4.		;
5.		;	6.		. 7.		.

147

Доказательство свойств.
1.	,				.
1.	,				.
2.			.
2.			.
3.				.
3.				.
4.		.


5.					;
5.					;

6.				;	.
					.

7.						так как		.
7.						так как		.

Замечание.

Свойства 5 и 6 справедливы для любого конечного числа слагаемых и конечного числа множителей:

5’.

6’.

В частности, при имеем:

так как

Следствие 4.

Пусть

- многочлен от комплексной

переменной с вещественными коэффициентами ,

. Тогда

Доказательство.

так как

. Следствие доказано.

148

§ 2. Геометрическое представление комплексных чисел.

Введем для удобства новые обозначения для комплексных чисел:

	,	,	.
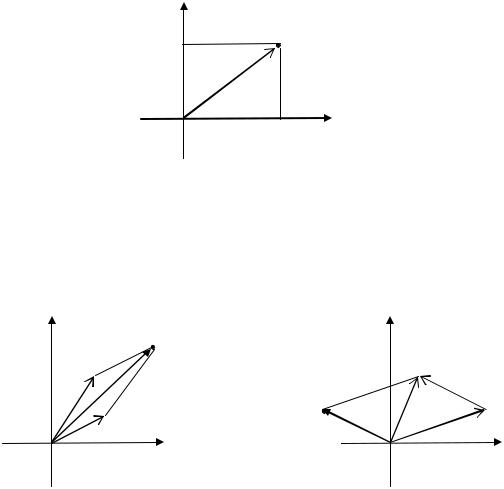
Возьмем на плоскости прямоугольную систему координат				. Тогда каждое
комплексное число		может быть изображено на этой плоскости точкой
или радиус-вектором		, координатами которых являются вещественная и
мнимая компоненты этого числа.
Очевидно, и обратно	каждой точке		на плоскости или радиус-вектору

соответствует вполне определенное комплексное число. В связи с этим рассматриваемую плоскость называют комплексной плоскостью.

	Вещественные числа	изображаются на оси , а чисто мнимые числа
	изображаются точками на оси . Поэтому ось абсцисс называют
вещественной осью, а ось ординат		мнимой осью. Начало координат соответствует
числу	.

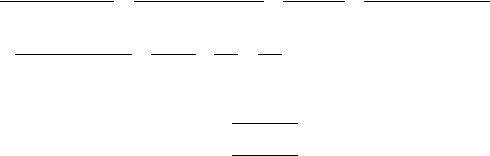
Если комплексные числа изображать радиус-векторами, то сумме этих чисел будет соответствовать сумма векторов, а разности чисел - разность векторов.

Модуль и аргумент комплексного числа.

Наряду с прямоугольной системой координат введем также и полярную систему

координат на плоскости, принимая точку	за полюс, а вещественную ось за полярную
ось. Тогда полярными координатами точки	являются	- длина ее радиус-

вектора, и полярный угол , образованный положительным направлением полярной оси и радиус-вектором данной точки.

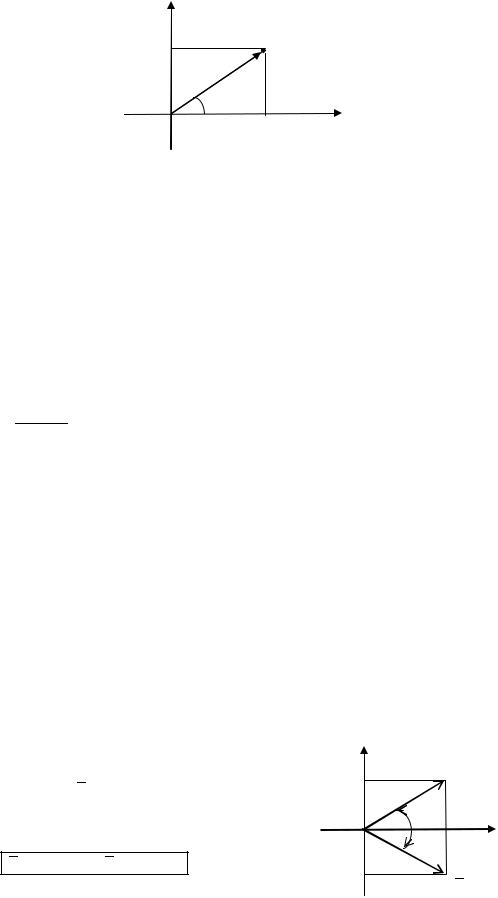
149

Величина называется модулем комплексного числа					и обозначается	;
величина называется аргументом комплексного числа и обозначается						.
Связь между прямоугольными и полярными координатами, как известно,
выражается следующими формулами:

	,	,		при	;
	,	,		при	;
если	, то		;
если	, то		;
при этом	,		(или		).

Следовательно, модуль и аргумент комплексного числа вычисляются по формулам:

	,				при	, где		.

	Аргумент комплексного числа определен не однозначно, так как угол между
двумя направлениями можно вычислять с точностью до слагаемых, кратных								.
	Множество всех значений аргумента комплексного числа обозначают							:
		,		, где		(или		).
	При этом	называют главным значением аргумента комплексного числа.
	Для вещественных положительных чисел					равен ; для вещественных
отрицательных чисел		равен	; для чисто мнимых чисел				равен		или	;

для	аргумент не определен.

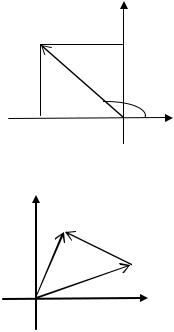
Комплексно-сопряженные числа

и имеют

равные модули и противоположные аргументы:

			150
Пример.
Найти модуль и аргумент (его главное значение) комплексного числа			.
Решение.

		;
		;
		;
		.
		.

Ответ:	,	.

Расстояние между точками

комплексной плоскости	и	равно
модулю разности чисел	и	:
	.

Например, расстояние между точками	и		равно:

		.

Для любых комплексных чисел и справедливы неравенства треугольника:

Геометрический смысл этих неравенств заключается в том, что длина стороны треугольника не превосходит суммы длин двух других его сторон, а разность длин двух сторон не превосходит длины третьей стороны.

Неравенство треугольника, очевидно, обобщается и на случай слагаемых в следующем виде:

§ 3. Основные множества на комплексной плоскости.

Рассмотрим характерные множества на комплексной плоскости, которые задаются некоторыми условиями (равенствами и неравенствами) и имеют важное значение при изучении теории функций комплексной переменной.

1. Окружности радиуса

- с центром в начале координат;

- с центром в точке .

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2315 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в папке Учебники

#
27.08.20203.23 Mб23Введение в мат.анализ.pdf
#
27.08.20203.47 Mб25Линейная алгебра и аналитическая геометрия.pdf