
|
|
41 |
Определение. |
Графиком функции |
называется множество точек на плоскости |
с координатами |
, где |
. Обозначение: . |
Графический способ используется, например, при изображении данных с какогонибудь прибора на экране монитора.
График функции, как правило, представляет собой некоторую кривую; но есть такие функции, графики которых устроены столь сложно, что изобразить их невозможно. Ниже нам встретятся такие примеры.
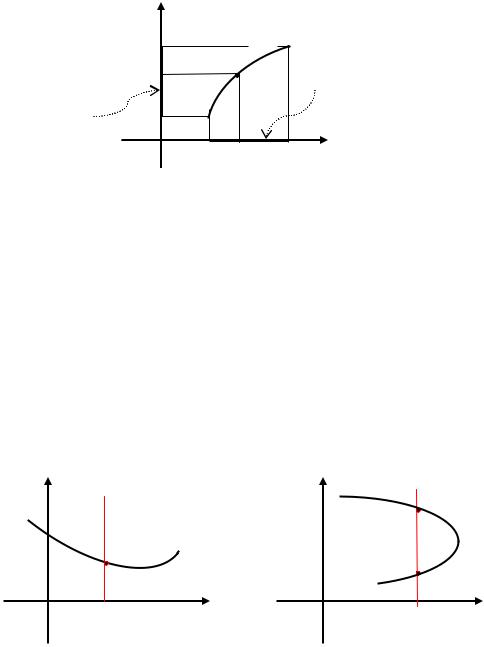
Следует заметить, что не любая кривая на плоскости может быть графиком какойнибудь функции . Дело в том, что на графике не может быть различных точек с одной и той же абсциссой, так как каждому значению соответствует единственное значение . Визуально это означает, что любая вертикальная прямая должна пересекать кривую не более чем в одной точке.
Например, ниже на рисунке ) кривая может быть графиком, а на рисунке б) - не может быть графиком никакой функции вида .
) график |
б) не график |
Если график функции известен, то область определения и область значений |
|
можно найти путем проектирования графика |
на оси координат (см. рис. выше). |
3). Аналитический способ. Это основной способ задания функции в математическом анализе. Функция задается с помощью формул, связывающих зависимую и независимую переменные.
При аналитическом способе функция может быть задана:
) явно: |
; б) неявно: |
; в) параметрически: |
. |
42
Неявное и параметрическое задание функций рассматриваются в разделе
Дифференциальное и интегральное исчисление функций |
математического анализа. |
|
Здесь мы ограничимся функциями, заданными явно: |
. |
|
При явном задании функция может быть определена одной формулой, а может |
||
быть и разными формулами на разных участках области определения. |
||
Например: |
|
|
|
|
|
, |
. |
|
|
|
|
Кроме табличного, графического и аналитического способов задания функций есть также и другие способы, например: алгоритмический, с помощью словесного описания и т.д.
Примеры функций.
Вэлементарной математике подробно изучаются известные функции:
-постоянная,
- |
|
|
линейная, |
- |
|
|
квадратичная, |
- |
|
, |
дробно-линейная, и многие другие. |
|
Рассмотрим некоторые примеры других функций.
1). Целая часть числа: |
. |
|
|
Если |
, где |
, то |
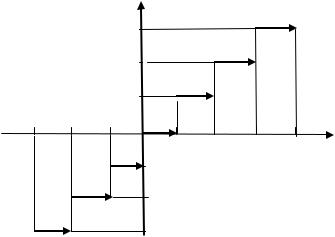
. График функции (стрелки на графике |
указывают на точки, не принадлежащие графику) представляет собой ступенчатую фигуру:
1 2
Область определения: |
; область значений: |
. |
|
2). Дробная часть числа: |
. |
|
|
Здесь |
. Если |
, где , то |
. Заметим, что |
. |
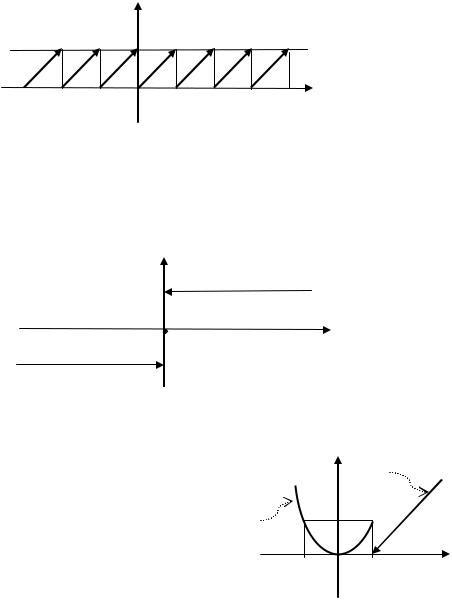
График функции (стрелки на графике указывают на точки, не |
||
принадлежащие графику): |
|
|
|
43
|
|
1 |
2 |
3 |
|
|
Область определения: |
; область значений: |
. |
||
3). |
(«сигнум» |
знак числа |
), где |
|
. |
График функции: |
|
|
|
|
|
Область определения: |
; область значений: |
. |
4). |
. График функции: |
Область определения: |
; область значений: |
|
. |
5). Функция Дирихле: |
, где |
, |
множество всех |
рациональных чисел.
Функция Дирихле принимает значение 1 во всех рациональных точках и значение 0 во всех иррациональных точках. Изобразить график этой функции не представляется возможным. Область определения: ; область значений: .
§5. Основные характеристики функции.
1). Четность, нечетность. |
|
|
|
Пусть функция |
имеет область определения , симметричную |
|
|
относительно точки , т.е. если |
, то и |
. |
|
Определение. Функция |
называется четной, если |
; |
|

44
Функция |
называется нечетной, если |
|
. |
|
Примеры четных функций: |
|
|
|
|
|
; |
; |
функция Дирихле. |
|
Примеры нечетных функций: |
|
|
|
|
|
; |
; |
функция «знак числа» . |
|
График четной функции симметричен относительно оси |
; график нечетной |
|||
функции симметричен относительно начала координат: |
|
|
||
) график четной функции. |
б) график нечетной функции. |
Если функция не является четной и не является нечетной, то она называется функцией общего вида.
2). Монотонность.
Пусть |
некоторое подмножество области определения функции |
: |
. |
||||||||
|
Определение. Функция |
|
называется возрастающей на множестве , если |
||||||||
|
, |
из неравенства |
следует неравенство |
и называется |
|||||||
строго возрастающей на множестве |
, если |
, |
из неравенства |
|
|||||||
следует неравенство |
|
|
. |
|
|
|
|
|
|
||
|
Обозначение: |
(или строго |
) на . |
|
|
|
|
||||
|
Определение. Функция |
|
называется убывающей на множестве |
, если |
|||||||
, |
|
из неравенства |
|
|
следует неравенство |
и называется |
|||||
строго убывающей на множестве , если |
, |
|
из неравенства |
следует |
|||||||
неравенство |
. |
|
|
|
|
|
|
|
|
||
|
Обозначение: |
(или строго |
) на . |
|
|
|
|
||||
|
Определение. Функция |
|
называется монотонной (строго монотонной) |
||||||||
на множестве , если она является возрастающей (строго возрастающей) или |
|||||||||||
убывающей (строго убывающей) на множестве . |
|
|
|
||||||||
|
Пример. Функция |
|
|
. Область определения: |
|
; |
|||||
|
|
|
|
||||||||
область значений: |
|
|
|
. |
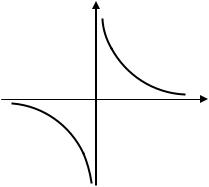
График функции: |
|
|
||||
45
Пусть |
, |
|
|
и |
; тогда |
|
|
|
|
|
|
|
|
|
|
; |
следовательно: |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
строго на |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть |
, |
|
|
и |
; тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
; |
следовательно: |
строго |
|
на |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Таким образом, |
функция |
|
|
строго |
на |
|
и строго |
на |
|
|
|
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Замечание. Неверно утверждать, что функция |
|
строго |
на |
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Действительно, пусть |
|
, |
|
|
|
|
|
|
|
; тогда |
|
, но |
|
|
|
|
|
|
, т.е. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исследуем на монотонность функции, приведенные в примерах §4. |
|
||||||||||||||||||||||||||||||
1). Целая часть числа: |
|
. Из графика функции видно, что |
|
|
|
(не строго) на . |
||||||||||||||||||||||||||
2). Дробная часть числа: |
. Из графика видно, что |
|
строго |
|
|
на каждом |
||||||||||||||||||||||||||
промежутке вида |
|
, где |
. |
Однако нельзя утверждать, что |
на (см. |
|||||||||||||||||||||||||||
последнее замечание). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3). |
|
. |
Из графика этой функции видно, что |
(не строго) на . |
|
|||||||||||||||||||||||||||
4). |
|
|
|
|
. Из графика этой функции видно, что |
|
|
|
|
|
строго |
на |
||||||||||||||||||||
|
, строго |
на |
|
и строго |
на |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5). Функция Дирихле: |
|
|
|
|
|
, где |
множество всех рациональных чисел. |
|||||||||||||||||||||||||
Эта функция не является монотонной ни на каком промежутке. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Замечание. Если функция строго монотонна на множестве |
, то она и (просто) монотонна |
|||||||||||||||||||||||||||||||
на этом множестве. Обратное утверждение, конечно, неверно. Поэтому не будет |
||||||||||||||||||||||||||||||||
ошибкой, если строго монотонную функцию назвать просто монотонной. |
|
|||||||||||||||||||||||||||||||
3). Ограниченность. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть |
|
некоторое подмножество области определения функции |
|
|
|
: |
. |
|||||||||||||||||||||||||
|
Определение. Функция |
|
|
называется ограниченной сверху на множестве , |
||||||||||||||||||||||||||||
если ограничено сверху множество |
|
|
|
|
|
|
|
|
, т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
Функция |
|
называется ограниченной снизу на множестве |
, если |
|
|
||||||||||
ограничено снизу множество |
|
, т. е. |
|
|
|
. |
|
|
|||||||
Функция |
|
называется ограниченной на множестве |
, если она ограничена |
||||||||||||
и сверху и снизу, т. е. |
|
|
|
|
. |
|
|
|
|
||||||
Замечание. Определение ограниченности функции равносильно следующему |
|
|
|||||||||||||
определению: функция |
|
ограничена на |
|
|
|
|
. |
|
|||||||
Определение. Функция |
называется неограниченной на множестве |
, |
|||||||||||||
если она не является ограниченной на этом множестве. |
|
|
|
|
|
||||||||||
Используя отрицание к понятию ограниченная функция , можно дать следующее |
|||||||||||||||
определение неограниченной функции: |
|
|
|
|
|
|
|
||||||||
функция |
не ограничена на |
|
|
|
. |
|
|
||||||||
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция |
|
|
|
|
|
ограничена |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
на промежутках вида: |
, |
, |
и |
, где |
|
или |
|
; |
|
||||||
и на промежутках вида: |
|
, |
, |
, |
, где |
|
и |
. |
|
||||||
Функция |
|
|
|
|
|
не ограничена |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
на промежутках вида: |
, |
, где |
; |
, |
, где |
и на |
|
|
|||||||
множествах вида |
, где |
. |
|
|
|
|
|
|
|||||||
Примеры ограниченных функций на . |
|
|
|
|
|
|
|
||||||||
Функции |
и |
|
ограничены на |
, т.к. |
|
и |
|
|
. |
||||||
Функции |
, |
функция Дирихле, |
|
также ограничены на . |
|||||||||||
Примеры ограниченных сверху (или снизу) функций на . |
|
|
|
|
|
||||||||||
, |
|
|
|
|
|
, |
|
|
ограничены снизу на |
|
|
|
. |
||
Квадратичная функция |
|
|
|
ограничена на |
сверху при |
|
и |
||||||||
ограничена на |
снизу при |
. |
|
|
|
|
|
|
|
||||||
Примеры неограниченных функций на . |
|
|
|
|
|
|
|
||||||||
Функции |
, |
, |
, |
, |
|
не ограничены на . |
|
|
|||||||
4). Периодичность. |
|
|
|
|
|
|
|
|
|
||||||
Определение. Функция |
называется периодической, если |
|
: |
|
|||||||||||
|
и |
|
. |
Число называется периодом функции. |
|
|
|
||||||||
Заметим, что если число |
является периодом функции, то и число |
, где |
|
||||||||||||
|
также будет периодом данной функции. Поэтому далее под периодом |
|
|
||||||||||||
подразумевается наименьший положительный период функции. |
|
|
|
|
|||||||||||
Примеры периодических функций:
|
|
|
47 |
- |
и |
, |
; |
- |
и |
, |
; |
- |
, |
. |
|
§6. Обратная функция.
Дана функция |
с областью определения |
и областью значений . |
||||
Определение. Функция |
называется взаимно-однозначной, если разным |
|||||
значениям аргумента соответствуют разные значения функции, т.е. |
|
|||||
|
|
|
|
|
. |
|
Если функция |
строго монотонна на , то она и взаимно-однозначна. |
|||||
Равенство: |
можно рассматривать как уравнение относительно |
|||||
неизвестной |
при любых фиксированных значениях . |
|
|
|||
Для взаимно-однозначной функции |
это уравнение имеет решение , |
|||||
причем оно единственно. Обозначим это решение как |
. |
|
||||
Тем самым возникает функция |
|
с областью определения |
и областью |
|||
значений . |
Функция |
называется обратной функцией к функции |
, а функции |
|||
иназываются взаимно-обратными функциями.
Заметим, что если |
обратная функция к функции |
, то |
обратная функция |
|||||||||||||
к функции |
, |
т.е. |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
строго монотонная функция; |
, |
; |
|
|
|
; |
|
||||||||
|
|
|||||||||||||||
следовательно: |
и |
|
|
|
|
взаимно-обратные функции. |
|
|||||||||
|
|
|
||||||||||||||
2. |
строго монотонная функция; |
, |
|
; |
|
; |
||||||||||
следовательно: |
и |
|
|
|
|
|
взаимно-обратные функции. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
3. |
строго монотонная функция; |
, |
; |
; |
|
|||||||||||
следовательно: |
и |
|
|
|
|
взаимно-обратные функции. |
|
|||||||||
|
|
|
|
|
||||||||||||
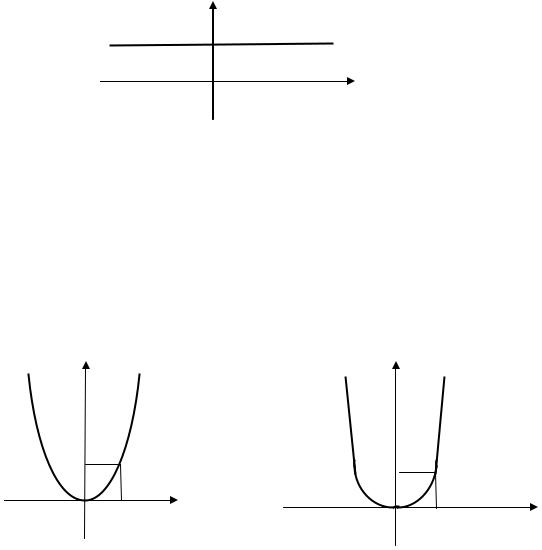
Графики взаимно-обратных функций. |
|
|
|
|
|
|
|
|
|
|||||||
Если |
|
и |
взаимно-обратные функции, то их графики |
|
||||||||||||
совпадают. Вместо записи |
для обратной функции можно применить |
|
||||||||||||||
обозначение |
. Тогда графики функций |
и |
|
уже не будут |
|
|||||||||||
совпадать. Как расположены друг относительно друга эти графики? |
|
|
|
|
|
|
||||||||||
Заметим, что если точка |
|
|
|
лежит на одном графике, то точка |
|
|||||||||||
лежит на другом графике, и наоборот. Но точки |
и |
симметричны относительно |
||||||||||||||
прямой |
(см. рис.) Следовательно, графики взаимно-обратных функций |
и |
||||||||||||||
|
симметричны относительно биссектрисы 1-го и 3-го координатных углов |
|
||||||||||||||
(т.е. относительно прямой |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||

48
Если функция |
не является строго монотонной на |
, то, как правило, можно |
||||||||||||||||||
выделить из области определения |
участки строгой монотонности. |
|
|
|
|
|
||||||||||||||
Пусть |
и |
|
строго монотонна на множестве |
. |
Рассмотрим новую |
|||||||||||||||
функцию, которую обозначим: |
такую, что |
|
|
|
|
|
|
|
|
. Эта новая функция |
||||||||||
отличается от функции |
|
лишь тем, что у нее другая область определения, а именно: |
||||||||||||||||||
множество . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция |
называется сужением функции |
на множество . Функция |
||||||||||||||||||
строго монотонна на своей области определения и, значит |
|
|
|
взаимно-однозначная |
||||||||||||||||
функция. Следовательно, для |
существует обратная функция |
. |
|
|
|
|
||||||||||||||
Пример. Функция |
|
не является строго монотонной на всей числовой оси, но |
||||||||||||||||||
является таковой на промежутках |
|
|
и |
. Рассмотрим сужения функции |
||||||||||||||||
на |
и на |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|||
, |
|
; |
|
|
|
|
. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом: |
|
, |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49
§7. Основные элементарные функции.
Косновным элементарным функциям относятся:
1)постоянная функция;
2)степенная функция;
3)показательная функция;
4)логарифмическая функция;
5)тригонометрические функции;
6)обратные тригонометрические функции.
1. Постоянная функция: , где произвольная константа.
График функции представляет собой прямую, параллельную оси абсцисс:
Область определения: |
, |
область значений: |
. |
|
|
2. Степенная функция: |
, |
где |
фиксированное число: |
. |
|
Для любой степенной функции |
|
выполняется равенство: |
. |
||
Свойства и графики степенных функций существенно зависят от того, какое число . Рассмотрим различные варианты.
1) |
натуральное число: |
|
. |
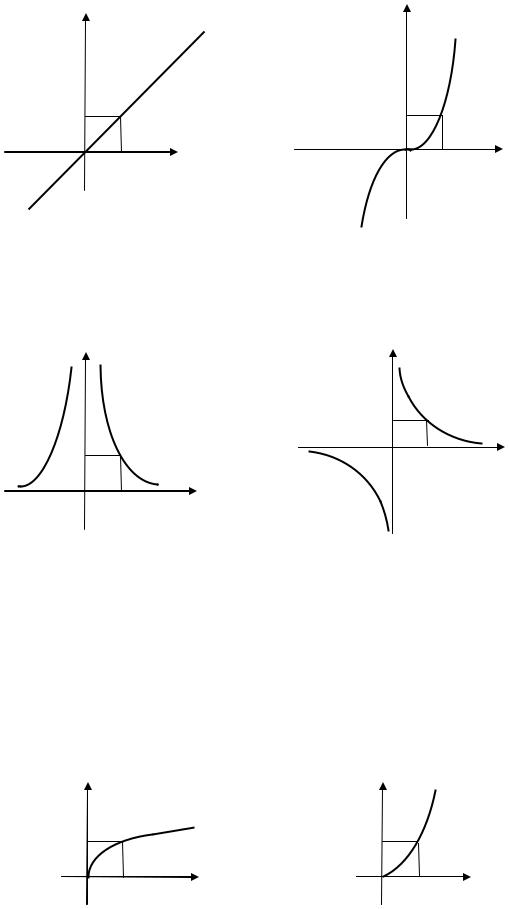
1.1) |
четное число: |
, |
. Графики функций: |
Свойства |
: |
, |
; четная; строго на |
и строго на |
; |
ограничена снизу; не периодическая. |
|
|
|||
1.2) |
|
нечетное число: |
, . Графики функций: |
|
|
50
Свойства |
: |
, |
|
|
; нечетная; строго |
на ; не ограничена; не |
|
||
периодическая. |
|
|
|
|
|
|
|
|
|
2) |
целое число: |
|
. Пусть |
, . |
|||||
Графики функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.1) |
четное число. |
|
|
|
|
|
|
|
|
|
|
||||||||
Свойства |
|
: |
|
|
, |
|
|
|
; четная; строго |
на |
и строго |
на |
|||||||
; |
ограничена снизу; не периодическая. |
|
|
|
|
|
|||||||||||||
2.2) |
нечетное число. |
|
|
|
|
|
|
|
|
|
|
||||||||
Свойства |
|
: |
|
|
, |
|
|
|
; нечетная; строго |
на |
и строго |
на |
|||||||
; |
не ограничена; не периодическая. |
|
|
|
|
|
|||||||||||||
3) |
|
рациональное число: |
|
|
|
|
|
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
3.1) |
|
|
, |
четное, |
|
|
|
|
. Графики функций: |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства |
: |
, |
; общего вида; строго на ; ограничена |
снизу; не периодическая. |
|
|
|
