
А. П. ПОТАПОВ
Введение в математический анализ
Теория, задачи и упражнения
|
Учебное пособие |
|
|
|
Оглавление |
|
|
I. Теория. |
|
|
|
Глава 1. |
Основные понятия |
… |
2 |
Глава 2. |
Последовательности и функции |
… |
32 |
Глава 3. |
Предел последовательности |
… |
60 |
Глава 4. |
Предел функции |
… |
90 |
Глава 5. |
Непрерывность функции |
… |
125 |
Глава 6. |
Комплексные числа |
… |
141 |
Глава 7. |
Алгебраические многочлены и рациональные дроби |
… |
177 |
II. Задачи и упражнения. |
|
|
|
Задачи к главе 1 |
… 190 |
||
Задачи к главе 2 |
… 191 |
||
Задачи к главе 3 |
… 195 |
||
Задачи к главе 4 |
… |
197 |
|
Задачи к главе 5 |
… |
200 |
|
Задачи к главе 6 |
… |
202 |
|
Задачи к главе 7 |
… |
206 |
|
Ответы |
|
… |
208 |
Литература |
|
… |
222 |
2
I. Теория.
Глава 1. Основные понятия.
Содержание
§ 1. |
Понятие множества …………………………………………………………….. |
3 |
§ 2. |
Логическая символика ……………………………………………………….. |
5 |
§ 3. |
Натуральные числа …………………………………………………………….. |
7 |
§ 4. Целые числа …………………………………………………………………………. |
9 |
|
§ 5. |
Рациональные числа …………………………………………………………… |
11 |
§ 6. |
Действительные числа ………………………………………………………… |
12 |
§7. Модуль числа ………………………………………………………………………. 14
§8. Числовая ось. Числовые промежутки …………………………………. 16
§9. Простейшие уравнения и неравенства с модулем …………….. 18
§ 10. Границы числовых множеств ……………………………………………… |
20 |
§ 11. Элементы комбинаторики …………………………………………………… |
23 |
§ 12. Бином Ньютона …………………………………………………………………... |
28 |
3
§ 1. Понятие множества.
Понятие множества является одним из основных неопределяемых понятий математики. Под множеством понимают совокупность, семейство, класс, набор и т.п. некоторых объектов, объединенных по какому-либо признаку. Например: множество целых чисел, множество точек на окружности, множество студентов института, множество файлов в данной папке и т.д.
Объекты, из которых состоит множество, называются его элементами. Множества
обозначают обычно заглавными буквами |
а их элементы - малыми буквами |
|
Если |
элемент множества то пишут: |
( принадлежит ); запись |
означает, что элемент не принадлежит . Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается символом .
Если элементами множества являются числа, то множество называется числовым множеством. Основные числовые множества:
множество всех натуральных чисел, множество всех целых чисел, множество всех рациональных чисел, множество всех действительных чисел, множество всех комплексных чисел.
Элементы множества обычно записывают в фигурных скобках, внутри которых они
перечислены: |
|
, или указано общее свойство, которым обладают все |
|
элементы данного множества, например: |
множество всех |
||
действительных чисел |
, удовлетворяющих неравенствам |
. |
|
Множество |
называется подмножеством множества |
, если каждый элемент |
|
множества является элементом множества , при этом записывают: |
|||
( включено в ). Пустое множество является подмножеством любого другого |
|||
множества ( |
, где |
любое множество). |
|
Для основных числовых множеств справедливы следующие включения:
.
Множества и |
называются равными и пишут: |
, если |
и |
. |
Множество |
, состоящее из конечного числа элементов, |
|
||
называется конечным множеством. Пустое множество также считается конечным множеством. Всякое множество, не являющееся конечным, называется бесконечным множеством. Например, множество всех натуральных чисел является бесконечным множеством.
Любое подмножество числового множества, отличное от пустого множества, также является числовым множеством. Например, промежуток [-1; 3) или набор чисел
являются числовыми множествами.
Всякое бесконечное множество является либо счетным, либо несчетным. Бесконечное множество называется счетным, если можно установить взаимно-
однозначное соответствие между этим множеством и множеством всех натуральных
4
чисел . Другими словами, бесконечное множество называется счетным, если все его
элементы можно пронумеровать: |
. |
Примерами счетных множеств являются само множество всех натуральных чисел |
|
, а также множество всех целых чисел |
и даже множество всех рациональных чисел |
(см. [6]). |
|
Бесконечное множество называется несчетным, если оно не является счетным. Примерами несчетных множеств являются множество всех действительных чисел , множество всех точек отрезка прямой и др. (см. [6]). Эти множества называются множествами мощности континуум.
Действия над множествами.
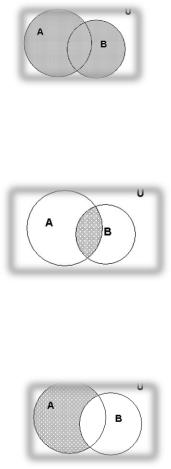
Объединением (или суммой) множеств и называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из этих множеств или .
Объединение (сумму) множеств обозначают |
(или |
): |
или |
. |
|
Пересечением (или произведением) множеств и называется множество, состоящее из всех тех элементов, которые принадлежат каждому из этих множеств и . Пересечение (произведение) множеств обозначают (или ):
и.
Разностью множеств и называется множество, состоящее из всех тех элементов множества , которые не принадлежат множеству . Разность множеств и обозначают :
и.
Пример 1. |
Пусть |
, |
. |
Тогда |
|
|
|
, |
, |
, |
. |
Пример 2. |
Пусть |
|
, |
. |
Тогда |
|
|
, |
|
, |
|
|
|
, |
|
. |
|
5
§ 2. Логическая символика.
При записи математических предложений (определений, утверждений и т.п.)
удобно использовать символы из математической логики: |
|
||||||||
|
|
символ импликации; |
|
символ эквивалентности; |
|||||
символ отрицания; |
|
символ конъюнкции; |
символ дизъюнкции; |
||||||
|
|
|
квантор всеобщности; |
|
|
квантор существования. |
|||
Пусть |
|
и |
некоторые математические высказывания или утверждения, |
||||||
относительно каждого из которых можно сказать истинно (верно) оно или ложно |
|||||||||
(неверно). Из этих утверждений можно составить новые утверждения: |
|||||||||
- |
|
|
означает: |
из |
следует |
, т.е. если истинно утверждение , то |
|||
истинно и утверждение . |
|
|
|
|
|
|
|||
- |
|
|
означает: |
эквивалентно |
, т.е. если истинно утверждение , то |
||||
истинно и утверждение и наоборот, если истинно утверждение |
, то истинно и |
||||||||
утверждение . |
|
|
|
|
|
|
|
||
- |
|
означает: |
не |
, т.е. если истинно утверждение |
, то ложно |
||||
утверждение |
, а если утверждение |
|
ложно, то утверждение |
истинно. |
|||||
-означает: , это утверждение истинно, если оба утверждения
истинны.
-означает: , это утверждение истинно, если истинно хотя бы
одно из утверждений |
|
. |
|
|
|
|
||
- |
|
|
означает: |
для любого элемента |
из множества справедливо |
|||
утверждение |
|
. |
|
|
|
|
|
|
- |
|
|
означает: |
существует элемент |
из множества |
, для которого |
||
справедливо утверждение |
. |
|
|
|
|
|||
Примеры математических утверждений. |
|
|
||||||
1). Даны действительные числа |
. |
|
|
|
||||
Утверждение |
: |
числа |
длины сторон некоторого треугольника , |
|||||
утверждение |
: |
|
. |
Тогда |
|
|
|
|
2). Даны натуральные числа |
и . |
|
|
|
|
|||
Утверждение |
: |
|
четное , |
|
|
|
||
утверждение |
: |
и |
четные . |
Тогда |
. |
|
||
3). Дана квадратная матрица . |
|
|
|
|
||||
Утверждение |
: |
|
невырожденная матрица |
, |
|
|||
утверждение |
: |
Существует обратная матница |
. Тогда |
. |
||||
4). Пусть |
окружность на плоскости с центром в точке С и радиуса . |
|
||||||
Тогда справедливо утверждение: |
|
. |
|
|||||
5). Пусть и |
ненулевые коллинеарные векторы. |
|
|
|||||
Тогда справедливо утверждение: |
|
. |
|
|||||
Рассмотрим примеры утверждений, которые являются отрицаниями других утверждений:
|
|
|
|
|
|
|
6 |
- |
|
|
. |
|
|
|
|
Это означает: утверждение |
не для всех |
выполняется |
равносильно |
||||
утверждению есть |
, для которого не выполняется |
. |
|
|
|||
- |
|
|
. |
|
|
|
|
Это означает: утверждение |
не существует |
, для которого выполняется |
|||||
равносильно утверждению для всех |
не выполняется |
|
. |
||||
Например: |
|
|
|
|
|
|
|
- не все целые числа делятся на |
равносильно утверждению |
есть целые числа, |
|||||
которые не делятся на |
; |
|
|
|
|
|
|
- не все квадратные матрицы имеют обратную матрицу |
равносильно утверждению |
||||||
есть квадратные матрицы, которые не имеют обратной ; - не все прямые на плоскости задаются линейным уравнением с угловым
коэффициентом равносильно утверждению |
есть прямые на плоскости, которые не |
задаются линейным уравнением с угловым коэффициентом ; |
|
- не существует вектора, модуль которого отрицателен равносильно утверждению |
|
модули всех векторов неотрицательны ; |
|
- не существует угла, синус которого больше 1 |
равносильно утверждению синусы всех |
углов не превосходят 1 . |
|
Математические утверждения делятся на аксиомы и теоремы (леммы, свойства). Аксиома - утверждение, устанавливающее некоторое свойство и принимаемое без доказательства. Теорема - утверждение, устанавливающее некоторое свойство и требующее доказательства.
Если теорема записывается в виде: |
(если , то |
), то |
условие |
|||
теоремы, а |
заключение теоремы. В этом случае утверждение |
|
называется |
|||
обратной теоремой, а утверждение |
|
называется прямой теоремой. |
||||
Если верна теорема |
, то |
называется достаточным условием для , а |
||||
необходимым условием для . Если верны и прямая и обратная теоремы, то |
||||||
называется необходимым и достаточным условием для |
(и наоборот). Фразу |
|||||
является необходимым и достаточным условием для |
можно заменить другой фразой: |
|||||
выполняется тогда и только тогда, когда выполняется |
или |
выполняется в том и |
||||
только в том случае, если выполняется . |
|
|
|
|
||
Необходимые и достаточные условия иначе называются признаками. Например, согласно теореме Кронекера-Капелли признаком (т.е. необходимым и достаточным условием) совместности системы линейных уравнений является равенство рангов основной и расширенной матриц этой системы.
Кроме указанных символов в математике часто применяются следующие
обозначения: " знак суммирования; |
" знак произведения. |
|
По определению: |
; |
. |
7
Например:
;
.
§ 3. Натуральные числа.
– множество всех натуральных чисел. Натуральные числа служат для счета конечного набора предметов.
Из -х арифметических действий: сложение, вычитание, умножение и деление только сложение и умножение определены для всех натуральных чисел. Результатом же вычитания или деления может получиться число, не являющееся натуральным числом.
Любое натуральное число, кроме 1, может быть либо простым, либо составным. Натуральное число называется простым, если оно делится нацело только на себя
и на 1. Например: 2; 3; 5; 7; 11; 13; … простые числа.
Натуральное число называется составным, если оно делится нацело на какое-либо другое число, отличное от самого себя и 1. Например: 4; 6; 8; 9; 10; 12; 14; 15; … составные числа.
Основная теорема арифметики. Любое натуральное число , большее 1, можно представить в виде произведения простых сомножителей с натуральными степенями, причем единственным образом:
|
|
|
|
. |
|
|
Например: |
|
|
|
|
|
|
Запись вида: |
|
|
называется каноническим |
|
||
разложением натурального числа . Здесь |
– простые числа, – натуральные числа |
|||||
( |
). |
|
|
|
|
|
Согласно основной теореме арифметики каноническое разложение |
единственно |
|||||
(с точностью до порядка сомножителей). |
|
|
|
|
||
Аксиома индукции. |
|
|
|
|
|
|
Пусть |
подмножество множества всех натуральных чисел: |
|
и пусть оно |
|||
обладает следующими 2-я свойствами: |
|
|
|
|
||
) 1 |
б |
справедливо утверждение: |
|
. |
||
|
Тогда: |
. |
|
|
|
|
На аксиоме индукции основан один из методов доказательства в математике - |
||||||
метод математической индукции. |
|
|
|
|
||
Метод математической индукции. |
|
|
|
|
||
Рассмотрим некоторое утверждение |
, зависящее от натурального числа . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
Обозначим через |
|
|
|
множество всех тех значений |
, для которых справедливо |
|
|||||||||||||||||||||||||||||
утверждение |
. Проверим выполнение условий ) и б |
аксиомы индукции, а именно: |
|
|||||||||||||||||||||||||||||||||
|
) при |
|
утверждение истинно; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
б если утверждение |
|
|
|
верно при |
|
|
то оно верно и при |
. |
|
|
|
|
|||||||||||||||||||||||
Если выполнение условий |
) и б) доказано, то |
|
|
|
, т.е. утверждение |
|
истинно при |
|||||||||||||||||||||||||||||
любых |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условие ) называется базой индукции, а условие б |
индукционным переходом. |
|
|||||||||||||||||||||||||||||||||
В некоторых случаях базой индукции служит условие: ) утверждение истинно при |
, |
|||||||||||||||||||||||||||||||||||
( |
или и т д |
|
. В этих случаях будет доказана истинность утверждения для всех |
|
||||||||||||||||||||||||||||||||
натуральных чисел |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 1. |
Докажем, что для всех |
|
выполняется равенство: |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
) при |
имеем: |
|
|
|
|
|
верное равенство; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
б пусть равенство верно при |
, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
докажем, что |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
равенство верно и для |
|
|
|
|
|
, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Для этого запишем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, что и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||
требовалось доказать. Следовательно, равенство верно для всех |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Пример 2. |
Докажем, что для всех |
|
выполняется равенство: |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
) при |
имеем: |
|
|
|
|
|
|
|
|
|
верное равенство; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
б пусть равенство верно при |
, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
докажем, что равенство верно и для |
|
, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Для этого запишем: |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
, что и требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Следовательно, равенство верно для всех |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Пример 3. |
|
Докажем неравенство Бернулли: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
для всех |
|
, где |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
) при |
имеем: |
|
|
|
|
|
|
|
|
|
|
верное неравенство; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
б пусть неравенство верно при |
|
|
, т.е. |
|
|
|
|
|
|
|
|
|
; |
докажем, что |
|
|||||||||||||||||||||
неравенство верно и для |
|
|
|
|
|
, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
. Для этого |
|
|||||||||||||||
запишем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
|
|
, что и требовалось доказать. Следовательно, неравенство |
|||
верно для всех |
. |
|
|
|
|
Замечание. |
|
|
|
|
|
Если |
, то неравенство Бернулли будет строгим неравенством для всех |
. |
|||
Для натуральных чисел можно ввести понятия факториала и двойного |
|
||||
факториала, которые обозначаются соответственно знаками |
" и ". |
|
|||
По определению факториала: |
|
|
|
||
|
|
произведение всех натуральных чисел от 1 до . |
|||
Например: |
|
|
|
|
|
; |
; |
; |
|
; |
. |
По определению двойного факториала: |
|
|
|
||
|
|
произведение всех натуральных чисел, взятых |
|||
через одного, от |
и ниже. |
Например: |
; |
|
. |
§ 4. Целые числа.
– множество всех целых чисел. Множество всех натуральных чисел является подмножеством множества всех
целых чисел: .
Из 4-х арифметических действий только сложение, вычитание и умножение определены для всех целых чисел, т.к. результатом этих действий с целыми числами также является целое число. Результатом же деления двух целых чисел не всегда будет
целое число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Если целое число делится на целое число |
, то будем писать |
, в |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
противном случае будем писать: |
. Например: |
|
|
|
|
|
|||||||||
|
Заметим, что |
|
|
для всех |
|
для всех |
, |
|
|
|
|||||
|
Числа: 0;1;2;3;4;5;6;7;8;9 – называются цифрами. |
|
|
|
|
||||||||||
|
Любое целое число |
|
можно записать с помощью этих десяти цифр: |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запись вида |
|
|
|
|
|
|
|
называется десятичной записью числа , где |
||||||
|
|
|
|
|
|
|
|
||||||||
|
– натуральное число, |
( |
|
|
) – цифры (однозначные числа): – цифра единиц, |
||||||||||
|
– цифра десяток, |
|
– цифра сотен и т.д. Если |
, то число |
|
двузначное, если |
|||||||||
|
, то число |
трехзначное и т.д. |
Например: |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
положительное трехзначное число ( |
), |
|||||
|
|
|
|
|
|
|
|
|
|
– отрицательное четырехзначное число |
|||||
( |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По десятичной записи числа можно определить делимость этого числа на любое |
||||||||||||||
однозначное число (кроме делимости на 7), а также на число . |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
Признаки делимости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Пусть |
|
|
|
|
|
десятичная запись числа. Тогда: |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2 |
|
|
; |
|
|
|
|
|
|
|
|
; |
|
|
|||||||||||
|
|
|
|
|
|
|
; |
|
|
|
5 |
; |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
8; |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
9 |
|
|
|
; |
|
10 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2, т.к. |
, т к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, т.к. 64 4; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
6, т.к. |
2 |
|
3; |
|
|
|
|
|
|
|
|
|
|
|||||
5, |
т к 4 |
5; |
|
|
|
и |
|
|
|
|
8 , т.к. 164 |
; |
|
|
||||||||||||||
9, т к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
т к |
|
|
|
|
|
||||||||||
|
|
|
Если |
|
|
|
|
|
, |
|
то возможно деление с остатком. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Теорема. Для любого целого числа |
и любого натурального числа |
существуют |
|||||||||||||||||||||||
целые числа и |
такие, что: |
|
|
где |
– остаток от деления |
на |
и |
|||||||||||||||||||||
|
|
|
– |
|
|
|
|
|
(При |
получаем: |
|
|
|
|
|
|
|
|
|
). |
|
|
||||||
|
|
|
Например, остаток от деления |
на |
равен |
, т.к. |
|
|
, а остаток от |
|||||||||||||||||||
деления |
на равен , т.к. |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Из этой теоремы при |
|
|
получаем следующее утверждение. |
|
|
||||||||||||||||||||
|
|
|
Следствие. Любое целое число |
можно представить в виде: |
|
|
||||||||||||||||||||||
(т.е. любое целое число либо делится на , либо при делении на дает остаток |
). |
|||||||||||||||||||||||||||
|
|
|
Числа вида |
|
называются четными, числа вида |
|
|
называются нечетными. |
||||||||||||||||||||
|
|
|
Понятие факториала: |
|
|
|
|
|
|
|
|
|
|
для отрицательных целых |
||||||||||||||
чисел |
не вводится, а для числа |
это понятие применяется. По определению: |
. |
|||||||||||||||||||||||||
|
|
|
Используя понятия четности и нечетности, можно уточнить понятие двойного |
|||||||||||||||||||||||||
факториала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Двойной факториал: |
|
|
|
|
|
|
|
|
|
|
|
произведение всех |
|
||||||||||||
натуральных чисел, не превосходящих |
и одной с ним четности. |
|
|
|||||||||||||||||||||||||
Если |
четное: |
|
|
, то двойной факториал есть произведение всех четных чисел от |
||||||||||||||||||||||||
2 до |
; если |
нечетное: |
|
|
|
, то это есть произведение всех нечетных чисел от |
||||||||||||||||||||||
1 до |
. Например: |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
. |
|
|
||||||||||
Могут быть полезны следующие формулы, связывающие двойной факториал с
обычным факториалом:
