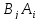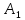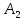- •4. Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий.
- •5. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Соотношение между ними.
- •Критерий решения игры в чистых стратегиях.
- •Доказательство утверждения .
- •Теорема об удовлетворительности игровой ситуации для игрока a.
- •Теорема об удовлетворительности игровой ситуации для игрока b
- •Равновесие в антагонистической игре.
- •Смешанные стратегии. Функция выигрыша и цена игры в смешанных стратегиях.
- •Теорема о существовании показателей эффективности и неэффективности смешанных стратегий в антагонистической игре.
- •Теорема о существовании нижней и верхней цен игры в смешанных стратегиях.
- •Теорема о соотношении нижней и верхней цен игры в чистых и смешанных стратегиях.
- •Основная теорема матричных игр Джона фон Неймана и седловая точка функции
- •Аналитическое решение игры 2×2 в смешанных стратегиях.
- •Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока a.
- •Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока b.
- •Геометрический метод нахождения цены игры 2×n и оптимальных стратегий игрока a.
- •Геометрический метод нахождения цены игры m×2 и оптимальных стратегий игрока b.
- •2)В общем случае схема решения игры 2xn или nx2 графическим методом состоит в следующем.
- •Доминирование смешанных стратегий для игрока a.
- •Доминирование смешанных стратегий для игрока b.
- •Решение матричной игры m×n сведением к задаче линейного программирования для игрока a.
- •Решение матричной игры m×n сведением к задаче линейного программирования для игрока b.
- •Основные понятия и определения теории игр с природой.
- •Игры с природой. Показатель благоприятности состояния природы. Риск игрока, принимающего решение. Матрица рисков. Принятие решений в условиях риска и неопределённости.
- •Критерий Байеса оптимальности чистых стратегий относительно выигрышей.
- •Критерий Байеса оптимальности чистых стратегий относительно рисков.
- •Критерий Лапласа оптимальности чистых стратегий относительно выигрышей.
- •Критерий Лапласа оптимальности чистых стратегий относительно рисков.
- •Критерий (крайнего пессимизма) Вальда оптимальности чистых стратегий.
- •Максимаксный критерий (крайнего оптимизма) оптимальности чистых стратегий.
- •Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей.
- •Определение показателей оптимизма и пессимизма игрока, принимающего решения по критерию Гурвица относительно выигрышей.
- •Учёт выигрышей по критерию Гурвица крайним пессимистом, крайним оптимистом и нейтралом.
- •Критерий Севиджа
- •Миниминный критерий.
- •Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно рисков.
- •Критерий Гермейера оптимальности чистых стратегий
- •Критерий Ходжа – Лемана оптимальности чистых стратегий относительно выигрышей.
- •Основные понятия и определения в теории неантагонистических (бескоалиционных) игр. Способы задания неантагонистической игры.
- •Стратегическая форма игры. Чистые и смешанные стратегии игроков в неантагонистических (бескоалиционных) играх. Доминирование стратегий.
- •Равновесие по Нэшу в чистых стратегиях.
- •Семейная пара принимает решение о месте куда они могут пойти в свободное время. Так он предлагает футбол, а она балет
- •Равновесие по Нэшу в смешанных стратегиях.
- •46. Аналитическое решение биматричных игр 2×2.
- •Аналогичный анализ можно провести для второго игрока.
- •47. Геометрическое решение биматричных игр 2×2
- •48. Модель дуополии по Курно.
- •49. Модель дуополии по Бертрану.
- •50. Модель «Проблема общего».
- •51. Оптимальность по Парето в неантагонистических (бескоалиционных) играх.
- •52. Позиционная форма игры.
- •53. Понятие о конечных играх с совершенной информацией.
- •54. Стратегическая форма позиционной игры с совершенной информацией.
- •55. Равновесие по Нэшу в позиционной игре с совершенной информацией.
- •56. Обратная индукция и позиционные игры с совершенной информацией.
- •57. Модель дуополии по Штакельбергу.
- •58. Модель последовательного торга.
- •59. Модель «инвесторы и банк».
Решение матричной игры m×n сведением к задаче линейного программирования для игрока a.
Пусть дана матричная игра с матрицей А порядка m х n.
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
А=
Po=(p1o,p2o,…,pmo)
 ,
,
Если игрок А применяет любую смешанную стратегию P=(p1,p2,…,pm) против любой чистой стратегии Bj игрока В, то он получает выигрыш
F(P,Bj)=a1jp1+a2jp2+…+anjpm, j=1,2,…,n
 .
.

Разделим каждое неравенство на V>0 и введем
x1=p1/v, x2=p2/v,…,xm=pm/v

Разделив
на V>0
равенство
 ,
получим выражениеx1+x2+…+xm=1/v
,
получим выражениеx1+x2+…+xm=1/v
Получаем задачу линейного программирования для игрока А:
x1+x2+…+xm->min(поскольку первый игрок стремится найти такие значения хi и, следовательно, pi , чтобы цена игры v была максимальной)

Po=(p1o=x1o*V, p2o=x2o*V,…,pmo=xmo*V)
Решение матричной игры m×n сведением к задаче линейного программирования для игрока b.
Пусть дана матричная игра с матрицей А порядка m х n.
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
А=
Qo=(q1o,q2o,…,qno)

Если игрок В применяет любую смешанную стратегию Q=(q1,q2,…,qm) против любой чистой стратегии Ai игрока A, то он получает проигрыш
F(P,Bj)=a1jq1+a2jq2+…+anjqm, j=1,2,…,n
 .
.

Разделим каждое неравенство на V>0 и введем
y1=q1/v, y2=q2/v,…,ym=qm/v

Разделив
на V>0
равенство
 ,
получим выражениеy1+y2+…+ym=1/v
,
получим выражениеy1+y2+…+ym=1/v
Получаем задачу линейного программирования для игрока В:
y1+y2+…+ym->max (поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры v была наименьшей)
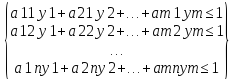
Qo=(q1o=y1o*V, q2o=y2o*V,…,qmo=ymo*V)
Основные понятия и определения теории игр с природой.
Во многих задачах финансово-экономической сферы принятие решения осложняется наличием неопределенности, заключающейся в неполноте информации об окружающей среде. Такую неопределенность могут порождать различные причины. Это могут быть действительные природные физические (климатические), биологические, химические, социальные и другие процессы, которые сопровождают экономическую деятельность, политика гос-ва и др. Поэтому в таких задачах принятие решения зависит от реальных условий, которые называют в соответствующей математической модели «природой». Саму же модель называют «игрой с природой». «Природа» может выступать как антагонистическая сторона, а может как кооперативная среда. Игру с природой можно определить как парную игру, в которой сознательный игрок А, заинтересованный в наиболее выгодном для него исходе игры, выступает против участника, совершенно безразличного к результату – природа (обозначим его П). Очевидно, что при решении игр с природой достаточно найти наилучшие рекомендации только для игрока А, потому как природа в рекомендациях не нуждается, развиваясь в соответствии с определенными законами независимо от того, удобно это человеку или нет.