59. Модель «инвесторы и банк».

Представим следующую ситуацию. Два инвестора вкладывают по D долларов в банк. Банк инвестировал эти средства в долгосрочный проект. Если форс-мажорные обстоятельства заставляют банк ликвидировать свои инвестиции до того, как проект «созревает», то он покрывает некоторую сумму , где. Если банк позволяет проекту «созреть», то проект принесёт,.

Есть два периода, когда вкладчики могут забрать свой вклад: период 1 – до «созревания», период 2 – после созревания. Для упрощения не будем учитывать дисконтирование. Если оба вкладчика забирают вклады в период 1, то оба получают по r и игра заканчивается. Если только один вкладчик забирает в период 1, то он получает D, а второй получ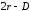ает . Наконец, если ни один вкладчик не забирает в период 1, то проект «созревает», и оба вкладчика забирают свои деньги в период 2, и каждый получает по R. Если только один вкладчик забирает деньги в период 2, то он получает , другой получаетD. Если, наконец, ни один не забирает в период 2, то банк возвращает по R каждому.

Дерево игры изображено на рис. 8.16.

Рис. 8.16.

Без строгой формализации игру в период 1 можно изобразить следующим образом:

	Забирать	Не забирать
Забирать	(r, r)	(D, 2r − D)
Не забирать	(2r − D, D)	(Шаг 2)

Для периода 2:

	Забирать	Не забирать
Забирать	(R, R)	(2R − D, D)
Не забирать	(D, 2R − D)	(R, R)

Рассмотрим внимательно матрицу для периода 2. Поскольку и, то в соответствии с принципом последовательной рациональности можем перейти к матрице для периода 1:

	Забирать	Не забирать
Забирать	(r, r)	(D, 2r − D)
Не забирать	(2r − D, D)	(R, R)

Т.к. и, то получаем два равновесия по Нэшу, дающие выигрыши (r, r) и (R, R). Принцип рационализации даёт нам окончательное решение (R, R).