11. Основные понятия и определения в теории неантагонистических (бескоалиционных) игр. Способы задания неантагонистической игры.

Некооперативная или бескоалиционная игра, это система    Г= (a_ij,b_ij)=(H^a(A_i,B_j), H^b(A_i,B_j)), где A_i и B_j принадлежат Sa и Sb соответственно, а H^a и H^b функции выигрыша. Sa и Sb – множество стратегий игрока А и В Sa= {A1,A2, … , Am}, Sb = {B1,B2, … , Bn}.

Бескоалиционное поведение, когда соглашения между участниками запрещены правилами, а кооперативное поведение разрешается в форме выбора совместных стратегий.

Интересы игроков могут пересекаться, быть взаимовыгодными обоим игрокам, в то время как в антагонистическом конфликте это не представляется возможным.

Матрица выигрышей двух игроков в бескоалиционной игре имеет следующий вид S= S^a x S^b:

А\В	B1	…	Bn
A1	(a11,b11)	…	(a1n,b1n)
…	…	…	…
Am	(am1,bm1)	…	(amn,bmn)

Неантагонистические игры, как и антагонистические, могут быть как конечные, так и бесконечные. Эта характеристика игры зависит от количества чистых стратегий игроков (S₁, S₂, … ,S_k где k- количество игроков, конечны)

Способы задания игр:

• стратегическая(нормальная, матричная)

• позиционная форма (форма дерева)

11. Стратегическая форма игры. Чистые и смешанные стратегии игроков в неантагонистических (бескоалиционных) играх. Доминирование стратегий.

В теории игр, игра в нормальной форме (или стратегической форме) состоит из трех элементов: множества игроков, множества чистых стратегий каждого игрока, множества платежных функций каждого игрока. Таким образом, игру в нормальной форме можно представить в виде матрицы, которая имеет следующий вид S= S^a x S^b:

А\В	B1	…	Bn
A1	(a11,b11)	…	(a1n,b1n)
…	…	…	…
Am	(am1,bm1)	…	(amn,bmn)

Чистая стратегия даёт полную определённость каким образом игрок продолжит игру. В частности, она определяет результат для каждого возможного выбора, который игроку может придётся сделать. Пространством стратегий называют множество всех чистых стратегий доступных данному игроку.

Действие игрока, состоящее в случайном выборе одной из своих стратегии с определенной вероятностью, называется смешанной стратегией. Если Si – конечное множество чистых стратегий игрока i, то смешанная стратегия ∂i : Si → [0,1] ставит в соответствие каждой чистой стратегии Si вероятность ∂i(Si) >= 0 того, что она будет играться, причем сумма всех вероятностей равна 1.

Смешанная стратегию игрока "А"

SA =	A1 A2 p1 p2

где A₁, A₂ - стратегии игрока "A", а p₁, p₂ - соответственно вероятности (частоты), с которыми эти стратегии применяются, причем p₁ + p₂ = 1. Аналогично смешанная стратегию игрока "В"

SB =	B1 B2 q1 q2

где B₁, B₂ - стратегии игрока "B", а q₁, q₂ - соответственно вероятности, с которыми эти стратегии применяются, причем q₁ + q₂ = 1.

Существуют ситуации доминирования стратегий, т.е. ситуации, когда один из игроков никогда не будет применять одну стратегию в пользу другой, потому что та будет приносить ему больший выигрыш.

Итак, стратегии могут доминировать как строго, так и слабо.

Чистая стратегия k-го игрока строго доминируема (строго доминируется), если существует другая чистая стратегия такая, чтодля.

Чистая стратегия k-го игрока слабо доминируема (слабо доминируется), если существует другая чистая стратегия такая, чтодля.

Смешанная стратегия k-го игрока строго доминируема (строго доминируется), если существует другая чистая стратегия такая, чтодля.

Смешанная стратегия k-го игрока слабо доминируема (слабо доминируется), если существует другая чистая стратегия такая, чтодля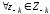.