11. Критерий Байеса оптимальности чистых стратегий относительно рисков.

Рассмотрим игру с природой с матрицей, в которой известны вероятности состояния природы q₁ .. q_n. При принятии решения в условиях риска можно пользоваться не только средними выигрышами, но и средними рисками. Составим матрицу рисков для матрицы исходной, использую формулу рисков:

r _i,j =

Показателем неэффективности стратегии S_i по критерию Байеса относительно рисков называется среднее значение (мат ожидание) рисков i-й строки матрицы А, вероятности которых, совпадают с вероятностями природы. Пусть средний риск при стратегии S_i равен

Показателем неэффективности стратегии по критерию Байеса относительно рисков называется среднее значение рисковi-й строки матрицы рисков: . Соответствующий критерий:.

Тогда оптимальной среди чистых стратегий по критерию Байеса относительно рисков является стратегия S_io, показатель неэффективности которой минимален, т.е. минимален средний риск.

Критерий Байеса относительно выигрышей и относительно рисков эквивалентны, т.е. если стратегия S_io является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот.

Пример для матрицы выигрышей.

	,	,	,
S1	2	6	4
S2	5	1	3

Из наибольшего числа каждого столбца вычитаем каждое число данного столбца. Стратегия S₁ является оптимальной по критерию Байеса относительно рисков, так как наименьший показатель неэффективности именно у этой стратегии (0,6). ,

	,	,	,
S1	3	0	0	0,6
S2	0	5	1	2,8

11. Критерий Лапласа оптимальности чистых стратегий относительно выигрышей.

Часто складывается такая ситуация, когда мы лишены возможности определить вероятности состояния природы.

Критерий основан на принципе недостаточного основания. Здесь все вероятности состояний природы признаются равновероятными: . Тогда показателем эффективности стратегиипо критерию Лапласа относительно выигрышей называется среднее арифметическое выигрышейi-й строки: .

Оптимальной среди чистых стратегий по критерию Лапласа относительно выигрышей считается стратегия с максимальным показателем эффективности:(матрица выигрышей),(матрица потерь).

Очевидно, что критерий Лапласа относительно выигрышей есть частный случай критерия Байеса относит выигрышей при .

				vi
S1	2	6	4	4
S2	5	1	3	3

Для матрицы выигрышей:,. Для матрицы потерь:

,

11. Критерий Лапласа оптимальности чистых стратегий относительно рисков.

Рассмотрим игру с природой с матрицей, в которой известны вероятности состояния природы q₁ .. q_n. При принятии решения в условиях риска можно пользоваться не только средними выигрышами, но и средними рисками. Составим матрицу рисков для матрицы исходной, использую формулу рисков:

r _i,j =

Критерий Байеса относительно рисков при равновероятных состояниях природы превращается в критерий Лапласа относительно рисков. Тогда величина, или более простая, представляет собой показатель неэффективности стратегииS_i по критерию Лапласа относительно рисков.

Следовательно, оптимальной среди чистых стратегий по критерию Лапласа относительно рисков является стратегия S_io, показатель неэффективностикоторой минимален:.

Пример для матрицы выигрышей.

S1	2	6	4
S2	5	1	3

Из наибольшего числа каждого столбца вычитаем каждое число данного столбца. Стратегия S₁ является оптимальной по критерию Байеса относительно рисков, так как наименьший показатель неэффективности именно у этой стратегии (0,6). ,

S1	3	0	0	3
S2	0	5	1	6
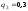