
- •4. Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий.
- •5. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Соотношение между ними.
- •Критерий решения игры в чистых стратегиях.
- •Доказательство утверждения .
- •Теорема об удовлетворительности игровой ситуации для игрока a.
- •Теорема об удовлетворительности игровой ситуации для игрока b
- •Равновесие в антагонистической игре.
- •Смешанные стратегии. Функция выигрыша и цена игры в смешанных стратегиях.
- •Теорема о существовании показателей эффективности и неэффективности смешанных стратегий в антагонистической игре.
- •Теорема о существовании нижней и верхней цен игры в смешанных стратегиях.
- •Теорема о соотношении нижней и верхней цен игры в чистых и смешанных стратегиях.
- •Основная теорема матричных игр Джона фон Неймана и седловая точка функции
- •Аналитическое решение игры 2×2 в смешанных стратегиях.
- •Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока a.
- •Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока b.
- •Геометрический метод нахождения цены игры 2×n и оптимальных стратегий игрока a.
- •Геометрический метод нахождения цены игры m×2 и оптимальных стратегий игрока b.
- •2)В общем случае схема решения игры 2xn или nx2 графическим методом состоит в следующем.
- •Доминирование смешанных стратегий для игрока a.
- •Доминирование смешанных стратегий для игрока b.
- •Решение матричной игры m×n сведением к задаче линейного программирования для игрока a.
- •Решение матричной игры m×n сведением к задаче линейного программирования для игрока b.
- •Основные понятия и определения теории игр с природой.
- •Игры с природой. Показатель благоприятности состояния природы. Риск игрока, принимающего решение. Матрица рисков. Принятие решений в условиях риска и неопределённости.
- •Критерий Байеса оптимальности чистых стратегий относительно выигрышей.
- •Критерий Байеса оптимальности чистых стратегий относительно рисков.
- •Критерий Лапласа оптимальности чистых стратегий относительно выигрышей.
- •Критерий Лапласа оптимальности чистых стратегий относительно рисков.
- •Критерий (крайнего пессимизма) Вальда оптимальности чистых стратегий.
- •Максимаксный критерий (крайнего оптимизма) оптимальности чистых стратегий.
- •Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей.
- •Определение показателей оптимизма и пессимизма игрока, принимающего решения по критерию Гурвица относительно выигрышей.
- •Учёт выигрышей по критерию Гурвица крайним пессимистом, крайним оптимистом и нейтралом.
- •Критерий Севиджа
- •Миниминный критерий.
- •Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно рисков.
- •Критерий Гермейера оптимальности чистых стратегий
- •Критерий Ходжа – Лемана оптимальности чистых стратегий относительно выигрышей.
- •Основные понятия и определения в теории неантагонистических (бескоалиционных) игр. Способы задания неантагонистической игры.
- •Стратегическая форма игры. Чистые и смешанные стратегии игроков в неантагонистических (бескоалиционных) играх. Доминирование стратегий.
- •Равновесие по Нэшу в чистых стратегиях.
- •Семейная пара принимает решение о месте куда они могут пойти в свободное время. Так он предлагает футбол, а она балет
- •Равновесие по Нэшу в смешанных стратегиях.
- •46. Аналитическое решение биматричных игр 2×2.
- •Аналогичный анализ можно провести для второго игрока.
- •47. Геометрическое решение биматричных игр 2×2
- •48. Модель дуополии по Курно.
- •49. Модель дуополии по Бертрану.
- •50. Модель «Проблема общего».
- •51. Оптимальность по Парето в неантагонистических (бескоалиционных) играх.
- •52. Позиционная форма игры.
- •53. Понятие о конечных играх с совершенной информацией.
- •54. Стратегическая форма позиционной игры с совершенной информацией.
- •55. Равновесие по Нэшу в позиционной игре с совершенной информацией.
- •56. Обратная индукция и позиционные игры с совершенной информацией.
- •57. Модель дуополии по Штакельбергу.
- •58. Модель последовательного торга.
- •59. Модель «инвесторы и банк».
Равновесие по Нэшу в чистых стратегиях.
Набор стратегий s=(s1, … , sn) образует равновесие по Нэшу если для любого Pk, (или ситуация s=(s1, … , sn) является равновесной по Нэшу)


где
s
 -
альтернатива стратегииa-ого
игрока
-
альтернатива стратегииa-ого
игрока 
 ,
, - игровая ситуация, которая сложилась
в результате выбора своих стратегий
всеми игроками кромеa-ого
- игровая ситуация, которая сложилась
в результате выбора своих стратегий
всеми игроками кромеa-ого
Пример . «Семейный спор».
Семейная пара принимает решение о месте куда они могут пойти в свободное время. Так он предлагает футбол, а она балет

Равновесие по Нэшу в смешанных стратегиях.
Обозначим набор смешанных стратегий s=(s1, … , sn) через σ=( σ1, … , σn).
Ситуация
(набор смешанных стратегий) σ=(σ1, … ,σn)
является равновесием по Нэшу в игре ={А,
{Σa}, {
={А,
{Σa}, { }},
если для любогоа=1, …,n
}},
если для любогоа=1, …,n
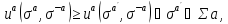
где
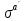 -
альтернатива стратегииa-ого
игрока
-
альтернатива стратегииa-ого
игрока
 ,
, - игровая ситуация, которая сложилась
в результате выбора своих стратегий
всеми игроками кромеa-ого.
- игровая ситуация, которая сложилась
в результате выбора своих стратегий
всеми игроками кромеa-ого.
Однако существуют дополнительные условия, при которых ситуация в смешанных стратегиях является равновесной по Нэшу.
Пусть
Sa+ Sa
– множество
чистых стратегий, которые игрок a
играет с положительной вероятностью в
ситуации σ=(
σ1,
… , σn).
Ситуация σ
является равновесной по Нэшу в смешанном
расширении
Sa
– множество
чистых стратегий, которые игрок a
играет с положительной вероятностью в
ситуации σ=(
σ1,
… , σn).
Ситуация σ
является равновесной по Нэшу в смешанном
расширении
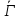 игры Г тогда и только тогда, когда для
всехa=1,
2, …, n
игры Г тогда и только тогда, когда для
всехa=1,
2, …, n
 Sa+
Sa+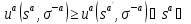 Sa+,
Sa+,
 Sa+
Sa+
Данные условия можно описать следующим образом:
Каждый игрок при данном распределении стратегий, которые играют его противники, безразличен между чистыми стратегиями, которые он играет с положительной вероятностью;
Эти чистые стратегии не хуже тех, которые он играет с нулевой вероятностью
46. Аналитическое решение биматричных игр 2×2.
|
|
B1 |
B2 |
|
A1 |
a11 |
a12 |
|
А2 |
a21 |
a22 |
А=
Сначала предположим, что матрица А имеет седловую точку aij, то есть элемент aij, наименьший в i-той строке и наибольший в j-том столбце. Тогда игра имеет решение в чистых стратегиях {Ai, Bj, V=aij}, где Ai и Bj- оптимальные стратегии соответственно игроков A и B, а V=aij – цена игры.
Рассмотрим случай, когда матрица [2x2]-не имеет седловой точки.
Тогда по теореме, каждый из игроков A и B обладает единственной оптимальной смешанной стратегией соответственно PO=(p1O,p2O) и QO=(q1O,q2O), где

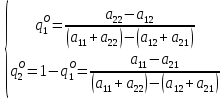
а цена игры (в смешанных стратегиях) V определяется формулой
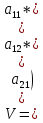
Пояснение (без строгого доказательства):
Рассмотрим функцию выигрыша игрока A более подробно:
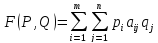 ,
,
 .
.
Примем также следующие обозначения:
 ,
,
 ,
,
 ,
,
 .
.
Пусть
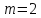 и
и ,
тогда функцию
,
тогда функцию можно переписать в виде:
можно переписать в виде:
 .
.
Представим
в явном виде функцию
 как линейную функцию с аргументом
(независимой переменной)q.
Получим следующее выражение:
как линейную функцию с аргументом
(независимой переменной)q.
Получим следующее выражение:
 .
.
Если
 ,
т.е. если
,
т.е. если
 ,
график функции имеет положительный
наклон. Это значит, что в ответ на действия
игрока A
игрок B
будем минимизировать свои потери
(минимизировать функцию
,
график функции имеет положительный
наклон. Это значит, что в ответ на действия
игрока A
игрок B
будем минимизировать свои потери
(минимизировать функцию
 ),
выбирая свою второю чистую стратегию,
т.е. реализуя смешанную стратегию
),
выбирая свою второю чистую стратегию,
т.е. реализуя смешанную стратегию ,
, .
В итоге исход игры определится результатом
.
В итоге исход игры определится результатом .
.
Если
 ,
т.е. если
,
т.е. если
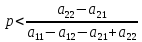 ,
график функции имеет отрицательный
наклон. Это значит, что в ответ на действия
игрока A
игрок B
будем минимизировать функцию
,
график функции имеет отрицательный
наклон. Это значит, что в ответ на действия
игрока A
игрок B
будем минимизировать функцию
 ,
выбирая свою первую чистую стратегию
,
выбирая свою первую чистую стратегию ,
, .
.
В
итоге исход игры определится результатом
 .
.
В итоге приходим к системе, решая которую, получим формулы, представленные в утверждении теоремы.

