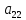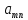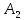- •4. Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий.
- •5. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Соотношение между ними.
- •Критерий решения игры в чистых стратегиях.
- •Доказательство утверждения .
- •Теорема об удовлетворительности игровой ситуации для игрока a.
- •Теорема об удовлетворительности игровой ситуации для игрока b
- •Равновесие в антагонистической игре.
- •Смешанные стратегии. Функция выигрыша и цена игры в смешанных стратегиях.
- •Теорема о существовании показателей эффективности и неэффективности смешанных стратегий в антагонистической игре.
- •Теорема о существовании нижней и верхней цен игры в смешанных стратегиях.
- •Теорема о соотношении нижней и верхней цен игры в чистых и смешанных стратегиях.
- •Основная теорема матричных игр Джона фон Неймана и седловая точка функции
- •Аналитическое решение игры 2×2 в смешанных стратегиях.
- •Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока a.
- •Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока b.
- •Геометрический метод нахождения цены игры 2×n и оптимальных стратегий игрока a.
- •Геометрический метод нахождения цены игры m×2 и оптимальных стратегий игрока b.
- •2)В общем случае схема решения игры 2xn или nx2 графическим методом состоит в следующем.
- •Доминирование смешанных стратегий для игрока a.
- •Доминирование смешанных стратегий для игрока b.
- •Решение матричной игры m×n сведением к задаче линейного программирования для игрока a.
- •Решение матричной игры m×n сведением к задаче линейного программирования для игрока b.
- •Основные понятия и определения теории игр с природой.
- •Игры с природой. Показатель благоприятности состояния природы. Риск игрока, принимающего решение. Матрица рисков. Принятие решений в условиях риска и неопределённости.
- •Критерий Байеса оптимальности чистых стратегий относительно выигрышей.
- •Критерий Байеса оптимальности чистых стратегий относительно рисков.
- •Критерий Лапласа оптимальности чистых стратегий относительно выигрышей.
- •Критерий Лапласа оптимальности чистых стратегий относительно рисков.
- •Критерий (крайнего пессимизма) Вальда оптимальности чистых стратегий.
- •Максимаксный критерий (крайнего оптимизма) оптимальности чистых стратегий.
- •Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей.
- •Определение показателей оптимизма и пессимизма игрока, принимающего решения по критерию Гурвица относительно выигрышей.
- •Учёт выигрышей по критерию Гурвица крайним пессимистом, крайним оптимистом и нейтралом.
- •Критерий Севиджа
- •Миниминный критерий.
- •Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно рисков.
- •Критерий Гермейера оптимальности чистых стратегий
- •Критерий Ходжа – Лемана оптимальности чистых стратегий относительно выигрышей.
- •Основные понятия и определения в теории неантагонистических (бескоалиционных) игр. Способы задания неантагонистической игры.
- •Стратегическая форма игры. Чистые и смешанные стратегии игроков в неантагонистических (бескоалиционных) играх. Доминирование стратегий.
- •Равновесие по Нэшу в чистых стратегиях.
- •Семейная пара принимает решение о месте куда они могут пойти в свободное время. Так он предлагает футбол, а она балет
- •Равновесие по Нэшу в смешанных стратегиях.
- •46. Аналитическое решение биматричных игр 2×2.
- •Аналогичный анализ можно провести для второго игрока.
- •47. Геометрическое решение биматричных игр 2×2
- •48. Модель дуополии по Курно.
- •49. Модель дуополии по Бертрану.
- •50. Модель «Проблема общего».
- •51. Оптимальность по Парето в неантагонистических (бескоалиционных) играх.
- •52. Позиционная форма игры.
- •53. Понятие о конечных играх с совершенной информацией.
- •54. Стратегическая форма позиционной игры с совершенной информацией.
- •55. Равновесие по Нэшу в позиционной игре с совершенной информацией.
- •56. Обратная индукция и позиционные игры с совершенной информацией.
- •57. Модель дуополии по Штакельбергу.
- •58. Модель последовательного торга.
- •59. Модель «инвесторы и банк».
Доминирование смешанных стратегий для игрока a.
Один из способов упрощения игр основывается на принципе доминирования, который позволяет в некоторых случаях игру с матрицей А свести к эквивалентной игре с матрицей меньшего размера.
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
А=
Между
множеством
 смешанных (в том числе и чистых) стратегий
смешанных (в том числе и чистых) стратегий игрока А и выпуклыми комбинациями
игрока А и выпуклыми комбинациями

строк ( матрицы А, представляющими собой строки
матрицы А, представляющими собой строки выигрышей
выигрышей ,j=1,2,…,n,
игрока А в ситуациях
,j=1,2,…,n,
игрока А в ситуациях
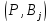 ,j=1,2,…,n,
устанавливается взаимно-однозначное
соответствие
,j=1,2,…,n,
устанавливается взаимно-однозначное
соответствие

из которого
ясно, что, в частности, каждой чистой
стратегии
 игрока А ставится во взаимно-однозначное
соответствиеk-я
строка
игрока А ставится во взаимно-однозначное
соответствиеk-я
строка
 матрицы А.
матрицы А.
Если для двух выпуклых комбинаций строк матрицы А

и

выполняются неравенства

то говорят, что строка (2) доминирует строку (1), а строка (1) доминирует строкой (2). Если каждое неравенство (3) является равенством, то строки (1) и (2) называют дублирующими. Если же каждое неравенство (3) является строгим, то говорят, что строка (2) строго доминирует строку (1), а строка (1) строго доминируется строкой (2).
Аналогичная
терминология используется и для
соответствующих стратегий игрока А. А
именно, если строка (2) доминирует,
соответственно дублирует, соответственно
строго доминирует строку (1), то говорят,
что стратегия
 доминирует, соответственно дублирует,
соответственно строго доминирует
стратегию
доминирует, соответственно дублирует,
соответственно строго доминирует
стратегию .
.
Таким образом, по данным определениям и для игрока А, предпочтительными оказываются доминирующие стратегии.
Доминирование смешанных стратегий для игрока b.
Один из способов упрощения игр основывается на принципе доминирования, который позволяет в некоторых случаях игру с матрицей А свести к эквивалентной игре с матрицей меньшего размера.
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
А=
Между
смешанными (в том числе и чистыми)
стратегиями
 игрока В и выпуклыми комбинациями
игрока В и выпуклыми комбинациями
 T,
T,

столбцов
 T
,
j=1,2,…,n,
матрицы А (Т- значок транспонирования),
представляющими собой столбцы
T
,
j=1,2,…,n,
матрицы А (Т- значок транспонирования),
представляющими собой столбцы
 T
T
проигрышей
Н( ,i=1,2,…,m,
игрока В в ситуациях (
,i=1,2,…,m,
игрока В в ситуациях ( ,i=1,2,…,m,
устанавливается взаимно-однозначное
соответствие
,i=1,2,…,m,
устанавливается взаимно-однозначное
соответствие
 T
,
T
,
из которого
видно, что, в частности, каждой чистой
стратегии
 ,l=1,2,…,n,
игрока В ставится во взаимно-однозначное
соответствие l-й
столбец
,l=1,2,…,n,
игрока В ставится во взаимно-однозначное
соответствие l-й
столбец
 T
матрицы А.
T
матрицы А.
Если для двух выпуклых комбинаций столбцов матрицы А
 T
T
и
 T
T
выполняются неравенства

то говорят,
что столбец (4) (стратегия
 доминирует столбец (5) (стратегию
доминирует столбец (5) (стратегию ,
а столбец (5) (стратегия
,
а столбец (5) (стратегия )
доминируется столбцом (4) (стратегией
)
доминируется столбцом (4) (стратегией ).
Если каждое неравенство (6) является
равенством, то столбцы (4) и (5) (стратегии
).
Если каждое неравенство (6) является
равенством, то столбцы (4) и (5) (стратегии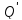 и
и )
называют дублирующими друг друга. Если
же каждое неравенство (6) является
строгим, то говорят, что столбец (4)
(стратегия
)
называют дублирующими друг друга. Если
же каждое неравенство (6) является
строгим, то говорят, что столбец (4)
(стратегия )
строго доминирует столбец (5) (стратегию
)
строго доминирует столбец (5) (стратегию ),
а столбец (5) (стратегия
),
а столбец (5) (стратегия )
строго доминируется столбцом (4)
(стратегией
)
строго доминируется столбцом (4)
(стратегией ).
).
Таким образом, по данным определениям для игрока В предпочтительными оказываются доминирующие стратегии.