11. Теорема о существовании показателей эффективности и неэффективности смешанных стратегий в антагонистической игре.

12. Теорема о существовании показателей эффективности и неэффективности смешанных стратегий в антагонистической игре.

Для каждой смешанной стратегии игрока существует ;(4.1)

Для каждой смешанной стратегии 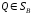игрока существует . (4.2)

Доказательство:

Для проведения доказательства введём понятие симплекса

Стандартным n-симплексом называется подмножество пространства действительных чисел, определяемое как

.

Его вершинами являются точки:

,

,

…

.

Сначала покажем, что симплекс является ограниченным замкнутым множеством, т.е. компактом.

Рассмотрим симплекс

в евклидовом пространстве . Так как норма векторав пространствеопределяется следующим образом:

,то для любой точки симплексасправедливо неравенство

,означающее ограниченность симплекса .

Пусть последовательность точек

, ,

сходится к точке при. Так как сходимость вявляется покоординатной, тоозначает, что,. Поскольку, то и.

Так как для каждогоk, то

.

Таким образом, предельная точка принадлежит симплексу, что доказывает его замкнутость.

Аналогично и симплекс – компакт в пространстве.

Если зафиксировать произвольную смешанную стратегию , то функция выигрышабудет функцией одного векторного аргумента, определённой на симплексе. Из аналитического выражения

,

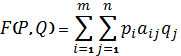
видно, что она непрерывна по аргументу Q на множестве , которое, как мы только что установили, является компактом, а непрерывная на компакте функция достигает своей нижней и верхней граней. Поэтому для любогосуществует (4.1), т.е. для любогонайдётся хотя бы одна точкатакая, что

.

Аналогично доказывается и существование (4.2).

Теорема доказана.

11. Теорема о существовании нижней и верхней цен игры в смешанных стратегиях.

Нижней ценой (или максимином) матричной игры в смешанных стратегиях называется величина

Верхней ценой (или минимаксом) матричной игры в смешанных стратегиях называется величина

Докажем существование нижней и верхней цен в смешанных стратегиях, т.е. достижимость максимума в (1) и минимума в (2). Необходимость этого доказательства возникает по причине бесконечности множеств S_A в (1) и S_B в (2).

Сначала докажем вспомогательные предложения.

Лемма 1. Соответствие, сопоставляющее каждой смешанной стратегии Р S_A игрока А показатель ее эффективности α(Р), является числовой функцией, определенной на симплексе S_A, аналитическое выражение которой задается равенством

Аналогично, соответствие β(Q), задаваемое формулой

является числовой функцией, определенной на симплексе S_B и ставящей в соответствие каждой смешанной стратегии Q S_B игрока В показатель ее неэффективности β(Q).

Доказательство. Для каждой смешанной стратегии PS_A в силу теоремы 1 - для каждой смешанной (в частности, чистой) стратегии Р S_A игрока А существует (достигается)

для каждой смешанной (в частности, чистой) стратегии QS_B игрока В существует (достигается)

существует число которое по определению минимума является единственным. Следовательно,α(Р) - числовая функция векторного аргумента Р, определенная на симплексе S_A.

Аналогичной аргументацией обосновывается, что

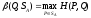является числовой функцией векторного аргумента Q, определенного на симплексе S_B.

Лемма 2. Функции α(Р) и β(Q) непрерывны в своих областях определения S_A и S_B.

Оставим без доказательства. Теперь докажем следующую теорему.

Теорема 2. Для любой конечной матричной игры существуют нижняя и верхняя цены игры в смешанных стратегиях. Доказательство. Так как функция α(Р) по лемме 2 непрерывна на компакте S_A, то она достигает на этом множестве своего максимума, т.е. существует нижняя цена игры в смешанных стратегиях:

Аналогичным образом обосновывается существование и верхней цены игры в смешанных стратегиях:

Смешанная стратегия P^ОS_A, максимизирующая показатель эффективности α(Р) (существование которой доказано в теореме 2), назовем максиминной смешанной стратегией игрока А. Таким образом, нижняя цена игрыесть (см. 1) показатель эффективности максиминной смешанной стратегииP^О:

В частном случае P^О =А_i0 является максиминной чистой стратегией игрока A.

Аналогично, смешанная стратегия Q^О S_B (существование которой доказано в теореме 2), минимизирующая показатель неэффективности β(Q), назовем минимаксной смешанной стратегией игрока В. Показатель неэффективности минимаксной смешанной стратегии Q^О равен верхней цене игры (см. 2)):

Если Q^О =B_j0, то B_j0является минимаксной чистой стратегией.