
- •4. Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий.
- •5. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Соотношение между ними.
- •Критерий решения игры в чистых стратегиях.
- •Доказательство утверждения .
- •Теорема об удовлетворительности игровой ситуации для игрока a.
- •Теорема об удовлетворительности игровой ситуации для игрока b
- •Равновесие в антагонистической игре.
- •Смешанные стратегии. Функция выигрыша и цена игры в смешанных стратегиях.
- •Теорема о существовании показателей эффективности и неэффективности смешанных стратегий в антагонистической игре.
- •Теорема о существовании нижней и верхней цен игры в смешанных стратегиях.
- •Теорема о соотношении нижней и верхней цен игры в чистых и смешанных стратегиях.
- •Основная теорема матричных игр Джона фон Неймана и седловая точка функции
- •Аналитическое решение игры 2×2 в смешанных стратегиях.
- •Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока a.
- •Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока b.
- •Геометрический метод нахождения цены игры 2×n и оптимальных стратегий игрока a.
- •Геометрический метод нахождения цены игры m×2 и оптимальных стратегий игрока b.
- •2)В общем случае схема решения игры 2xn или nx2 графическим методом состоит в следующем.
- •Доминирование смешанных стратегий для игрока a.
- •Доминирование смешанных стратегий для игрока b.
- •Решение матричной игры m×n сведением к задаче линейного программирования для игрока a.
- •Решение матричной игры m×n сведением к задаче линейного программирования для игрока b.
- •Основные понятия и определения теории игр с природой.
- •Игры с природой. Показатель благоприятности состояния природы. Риск игрока, принимающего решение. Матрица рисков. Принятие решений в условиях риска и неопределённости.
- •Критерий Байеса оптимальности чистых стратегий относительно выигрышей.
- •Критерий Байеса оптимальности чистых стратегий относительно рисков.
- •Критерий Лапласа оптимальности чистых стратегий относительно выигрышей.
- •Критерий Лапласа оптимальности чистых стратегий относительно рисков.
- •Критерий (крайнего пессимизма) Вальда оптимальности чистых стратегий.
- •Максимаксный критерий (крайнего оптимизма) оптимальности чистых стратегий.
- •Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей.
- •Определение показателей оптимизма и пессимизма игрока, принимающего решения по критерию Гурвица относительно выигрышей.
- •Учёт выигрышей по критерию Гурвица крайним пессимистом, крайним оптимистом и нейтралом.
- •Критерий Севиджа
- •Миниминный критерий.
- •Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно рисков.
- •Критерий Гермейера оптимальности чистых стратегий
- •Критерий Ходжа – Лемана оптимальности чистых стратегий относительно выигрышей.
- •Основные понятия и определения в теории неантагонистических (бескоалиционных) игр. Способы задания неантагонистической игры.
- •Стратегическая форма игры. Чистые и смешанные стратегии игроков в неантагонистических (бескоалиционных) играх. Доминирование стратегий.
- •Равновесие по Нэшу в чистых стратегиях.
- •Семейная пара принимает решение о месте куда они могут пойти в свободное время. Так он предлагает футбол, а она балет
- •Равновесие по Нэшу в смешанных стратегиях.
- •46. Аналитическое решение биматричных игр 2×2.
- •Аналогичный анализ можно провести для второго игрока.
- •47. Геометрическое решение биматричных игр 2×2
- •48. Модель дуополии по Курно.
- •49. Модель дуополии по Бертрану.
- •50. Модель «Проблема общего».
- •51. Оптимальность по Парето в неантагонистических (бескоалиционных) играх.
- •52. Позиционная форма игры.
- •53. Понятие о конечных играх с совершенной информацией.
- •54. Стратегическая форма позиционной игры с совершенной информацией.
- •55. Равновесие по Нэшу в позиционной игре с совершенной информацией.
- •56. Обратная индукция и позиционные игры с совершенной информацией.
- •57. Модель дуополии по Штакельбергу.
- •58. Модель последовательного торга.
- •59. Модель «инвесторы и банк».
56. Обратная индукция и позиционные игры с совершенной информацией.
Для того, чтобы внимательнее посмотреть на обратную индукцию в конечной игре с совершенной информацией, начнём с определения оптимального «действия» в последних вершинах дерева, где принимается решение (т.е. тех вершин, для которых «последователи» – это только терминальные вершины). Решение, принимаемое игроком в такой вершине, не зависит уже от стратегического взаимодействия и потому является простой задачей принятия решения. Затем мы может обратиться к «предпоследней» вершине и найти оптимальное решение там, предвидя, естественно, ход, который будет сделан в последней вершине. И так далее.
Рассмотрим следующий пример позиционной игры

Принимая оптимальные решения для третьего игрока в последних вершинах дерева, приходим к первой редуцированной игре следующего вида

Принимая оптимальное решение для второго игрока, получаем вторую редуцированную игру (

Игровая
ситуация
 является равновесной по Нэшу. Игрок
отклонившись в единоличном порядке от
своей оптимальной стратегии может лишь
ухудшить своё положение. Найденное
решение игры проведено в соответствии
с принципом последовательной
рациональности.
является равновесной по Нэшу. Игрок
отклонившись в единоличном порядке от
своей оптимальной стратегии может лишь
ухудшить своё положение. Найденное
решение игры проведено в соответствии
с принципом последовательной
рациональности.
57. Модель дуополии по Штакельбергу.
Дуополия по Штакельбергу – это модификация дуополии по Курно. Теперь мы считает, что есть лидер, который делает ход первым. Затем, зная этот выбор, другой игрок делает свой ход.
Итак, игра протекает следующим образом:
фирма 1 выбирает
 ;
;фирме 2 становится известна величина
 ,
и после этого она выбирает
,
и после этого она выбирает ;
;Выигрыш фирмы определяется формулой
 ,
, .
.
Для нахождения равновесия воспользуемся обратной индукцией. Определим сначала функцию реагирования фирмы 2, решая задачу
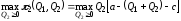 .
.
Привлекая
необходимое условие существования
экстремума получаем функцию реагирования
 .
То же самое было и в случае дуополии
Курно. Разница, однако, в том, чтодействительная,
а не гипотетическая функция реагирования
фирмы 2.
.
То же самое было и в случае дуополии
Курно. Разница, однако, в том, чтодействительная,
а не гипотетическая функция реагирования
фирмы 2.
Фирма 1, естественно, также может вычислить эту функцию реагирования, а, следовательно, задача фирмы 1 выглядит так:
 ,
,
что даёт
 и
и .
.
Прибыль в случае дуополии по Штакельбергу:
 ,
,
 .
.
Для сравнения в модели Курно:
 .
.
58. Модель последовательного торга.
Рассмотрим следующую игру. Игроки 1 и 2 торгуются о разделе 1 доллара: 1-й игрок предлагает некоторый способ деления, 2-й либо принимает это предложение, либо нет; если нет, то он предлагает способ деления, а 1-й принимает, либо нет и т.д.
Каждое предложение занимает один период, но при этом есть дисконтирующий множитель. Итак, формально рассмотрим следующую трёх-периодную игру.
1.а) В
начале первого периода игрок 1 предлагает
«свою долю»
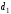 доллара, оставляя
доллара, оставляя игроку 2.
игроку 2.
1.b) Игрок 2 принимает предложение, тогда игра заканчивается, либо отклоняет его. В этом случае игра переходит ко 2-му периоду.
2.a)
В начале второго периода игрок 2 предлагает
долю
 ,
которую получает игрок 1, оставляя себе
,
которую получает игрок 1, оставляя себе .
.
2.b) Игрок 1 либо принимает предложение, либо нет. В последнем случае игра переходит к 3-му периоду.
3) Игроки
в третьем периоде получают доли
 ,
, ,
причёмd
задан экзогенно.
,
причёмd
задан экзогенно.
Решим
данную задачу с помощью обратной
индукции. Сначала вычислим, что происходит,
если дело доходит до 2-го периода. Игрок
1 может получить d,
если отклонит
 .
С учётом дисконтирования (мы сравниваем
стоимость в разных (соседних) периодах)
игрок 1 примет
.
С учётом дисконтирования (мы сравниваем
стоимость в разных (соседних) периодах)
игрок 1 примет тогда и только тогда, когда
тогда и только тогда, когда ,
, – коэффициент дисконтирования. Это
значит, что задача игрока 2 состоит в
выборе между получением
– коэффициент дисконтирования. Это
значит, что задача игрока 2 состоит в
выборе между получением и получением
и получением в следующем периоде. Дисконтированная
стоимость последнего действия есть
в следующем периоде. Дисконтированная
стоимость последнего действия есть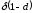 ,
что меньше, чем
,
что меньше, чем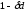 ,
а потому игрок 2 во втором периоде
предлагает
,
а потому игрок 2 во втором периоде
предлагает .
.
Таким
образом, если игра доходит до второго
периода, то 2-й игрок предложит
 ,
и игрок 1 примет это предложение.
,
и игрок 1 примет это предложение.
Однако
игрок 1 может предвидеть, что игрок 2
может получить
 во втором периоде, отклоняя предложение
во втором периоде, отклоняя предложение .
В первом периоде стоимость
.
В первом периоде стоимость с учётом дисконтирования составит
с учётом дисконтирования составит .
Значит, игрок 2 принимает
.
Значит, игрок 2 принимает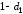 тогда и только тогда, когда
тогда и только тогда, когда ,
или
,
или .
.
Поэтому
задача игрока 1 в первом периоде состоит
в выборе между получением
 в этом периоде и получением
в этом периоде и получением в следующем периоде. Дисконтированная
величина
в следующем периоде. Дисконтированная
величина составляет
составляет ,
что меньше, чем
,
что меньше, чем .
Значит, оптимальное предложение в первом
периоде есть
.
Значит, оптимальное предложение в первом
периоде есть .
Следовательно, в первом периоде игрок
1 предлагает
.
Следовательно, в первом периоде игрок
1 предлагает ,
а игрок 2 принимает это предложение и
получает
,
а игрок 2 принимает это предложение и
получает .
Таким образом, выигрыш игроков есть
.
Таким образом, выигрыш игроков есть и
и соответственно.
соответственно.
