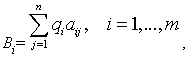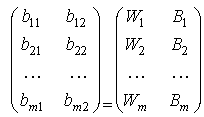- •4. Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий.
- •5. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Соотношение между ними.
- •Критерий решения игры в чистых стратегиях.
- •Доказательство утверждения .
- •Теорема об удовлетворительности игровой ситуации для игрока a.
- •Теорема об удовлетворительности игровой ситуации для игрока b
- •Равновесие в антагонистической игре.
- •Смешанные стратегии. Функция выигрыша и цена игры в смешанных стратегиях.
- •Теорема о существовании показателей эффективности и неэффективности смешанных стратегий в антагонистической игре.
- •Теорема о существовании нижней и верхней цен игры в смешанных стратегиях.
- •Теорема о соотношении нижней и верхней цен игры в чистых и смешанных стратегиях.
- •Основная теорема матричных игр Джона фон Неймана и седловая точка функции
- •Аналитическое решение игры 2×2 в смешанных стратегиях.
- •Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока a.
- •Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока b.
- •Геометрический метод нахождения цены игры 2×n и оптимальных стратегий игрока a.
- •Геометрический метод нахождения цены игры m×2 и оптимальных стратегий игрока b.
- •2)В общем случае схема решения игры 2xn или nx2 графическим методом состоит в следующем.
- •Доминирование смешанных стратегий для игрока a.
- •Доминирование смешанных стратегий для игрока b.
- •Решение матричной игры m×n сведением к задаче линейного программирования для игрока a.
- •Решение матричной игры m×n сведением к задаче линейного программирования для игрока b.
- •Основные понятия и определения теории игр с природой.
- •Игры с природой. Показатель благоприятности состояния природы. Риск игрока, принимающего решение. Матрица рисков. Принятие решений в условиях риска и неопределённости.
- •Критерий Байеса оптимальности чистых стратегий относительно выигрышей.
- •Критерий Байеса оптимальности чистых стратегий относительно рисков.
- •Критерий Лапласа оптимальности чистых стратегий относительно выигрышей.
- •Критерий Лапласа оптимальности чистых стратегий относительно рисков.
- •Критерий (крайнего пессимизма) Вальда оптимальности чистых стратегий.
- •Максимаксный критерий (крайнего оптимизма) оптимальности чистых стратегий.
- •Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей.
- •Определение показателей оптимизма и пессимизма игрока, принимающего решения по критерию Гурвица относительно выигрышей.
- •Учёт выигрышей по критерию Гурвица крайним пессимистом, крайним оптимистом и нейтралом.
- •Критерий Севиджа
- •Миниминный критерий.
- •Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно рисков.
- •Критерий Гермейера оптимальности чистых стратегий
- •Критерий Ходжа – Лемана оптимальности чистых стратегий относительно выигрышей.
- •Основные понятия и определения в теории неантагонистических (бескоалиционных) игр. Способы задания неантагонистической игры.
- •Стратегическая форма игры. Чистые и смешанные стратегии игроков в неантагонистических (бескоалиционных) играх. Доминирование стратегий.
- •Равновесие по Нэшу в чистых стратегиях.
- •Семейная пара принимает решение о месте куда они могут пойти в свободное время. Так он предлагает футбол, а она балет
- •Равновесие по Нэшу в смешанных стратегиях.
- •46. Аналитическое решение биматричных игр 2×2.
- •Аналогичный анализ можно провести для второго игрока.
- •47. Геометрическое решение биматричных игр 2×2
- •48. Модель дуополии по Курно.
- •49. Модель дуополии по Бертрану.
- •50. Модель «Проблема общего».
- •51. Оптимальность по Парето в неантагонистических (бескоалиционных) играх.
- •52. Позиционная форма игры.
- •53. Понятие о конечных играх с совершенной информацией.
- •54. Стратегическая форма позиционной игры с совершенной информацией.
- •55. Равновесие по Нэшу в позиционной игре с совершенной информацией.
- •56. Обратная индукция и позиционные игры с совершенной информацией.
- •57. Модель дуополии по Штакельбергу.
- •58. Модель последовательного торга.
- •59. Модель «инвесторы и банк».
Критерий Гермейера оптимальности чистых стратегий
При использовании этого критерия исходная платёжная матрица заменяется матрицей Гермейера. Каждый элемент матрицы мы домножаем на соответствующую вероятность j состояния природы.
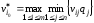 для матрицы
выигрышей,
для матрицы
выигрышей,
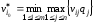 для матрицы
потерь.
для матрицы
потерь.
Критерий Гермейера применяют игроки не склонные к риску, т.к. каждая стратегия оценивается с точки зрения min по гарантиров. результата.
Состояние природы образует минимум а затем игрок выбирает стратегию которая принесёт ему максимальный результат. Т.е. он защищает себя.
Пример.
Исходная матрица
|
|
|
|
|
|
|
9 |
4 |
1 |
|
|
7 |
1 |
8 |
|
|
11 |
3 |
7 |
Далее умножаем каждый элемент в столбце на соответствующий коэффициент q. Получим следующую таблицу :
|
|
|
|
|
VGi в. |
VGi п. |
|
|
3,6 |
0,8 |
0,1 |
0,1 |
3,6 |
|
|
2,8 |
0,2 |
0,8 |
0,2 |
2,8 |
|
|
4,4 |
0,6 |
0,7 |
0,6 |
4,4 |
В столбце VGi в. Находим миним. Элементы по строкам , а в столбце VGi п. находим макс. Элементы.
Далее находим VGi в (maxmin) , и VGi п. (minmax)
Получаем следующий ответ : S*=S3 , V*=0,6 - выигрыш
S*=S2 , V*=2,8 - потеря
Критерий Ходжа – Лемана оптимальности чистых стратегий относительно выигрышей.
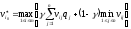 матрица
выигрышей
матрица
выигрышей
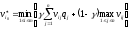 матрица
потерь
матрица
потерь
y- параметр отражающий степень доверия ЛПР к оценкам вероятностей состояния природы.
y
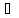 [0,1]
[0,1]
Чем выше у, тем выше доверие игрока А к оценкам вероятности. А следовательно от того как У зависит доминирует первое слагаемое или второе.
Критерий Ходжа-Лемана
1) Предположим, что матрицей выигрышей игрока А является матрица А.
2) Известны вероятности qi=p(Пj), j=1,…,n, состояний природы Пj, j=1,…,n, удовлетворяющие условию (1).
Таким образом, игроку А надлежит принимать решение в условиях риска.
3) Пусть l=2,
|
|
(11) |
показатель эффективности стратегии Аi по критерию Вальда,
|
|
(12) |
показатель эффективности стратегии Аi по критерию Байеса.
Матрица В примет вид
|
В= |
|
т.е. bi1=Wi, bi2=Bi, i=1,…,m.
4) Коэффициенты l1, l2 выбираются следующим образом:
|
l1=1-l, l2=l, где lÎ[0, 1]. |
(13) |
Очевидно, что эти коэффициенты удовлетворяют условию (2).
5) По формуле (3), с учетом (11), (12), и (13), показатель эффективности стратегии Аi по критерию Ходжа-Лемана равен:
|
Gi=libi1+l2bi2=(1-l)Wi+lBi=(1-l)aij+l qiaj i=1,…,m. |
(14) |
|
|
|
В правой части формулы (14) коэффициент lÎ[0, 1] есть количественный показатель степени доверия игрока А данному распределению вероятностей qi=p(Пj), j=1,…,n, состояний природы Пj, j=1,…,n, а коэффициент (1-l) характеризует количественно степень пессимизма игрока А. Чем больше доверия игрока А данному распределению вероятностей состояний природы, тем меньше пессимизма и наоборот.
6) Цену игры по критерию Ходжа-Лемана находим по формуле (4):
![]()
7) Оптимальной стратегией по критерию Ходжа-Лемана является стратегия Аk с наибольшим показателем эффективности:
Gk=G.
Отметим, что критерий Ходжа-Лемана является как-бы промежуточным критерием между критериями Байеса и Вальда. При l=1, из (14) имеем:Gi=Bi и потому критерий Ходжа-Лемана превращается в критерий Байеса. А при l=0, из (14): Gi=Wi и, следовательно, из критерия Ходжа-Лемана получаем критерий Вальда.
Пример.
Исходная матрица
|
|
q=0,4 П1 |
q=0,3 П2 |
q=0,1 П3 |
q=0,2 П4 |
|
S1 |
6 |
3 |
4 |
5 |
|
S2 |
4 |
3 |
6 |
5 |
Далее используя формулы –
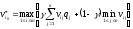 матрица
выигрышей
матрица
выигрышей
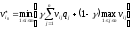 матрица
потерь
матрица
потерь
каждый элемент в столбце на соответствующий коэффициент q. Получим следующую таблицу :
|
Vi1*q1 |
Vi2*q2 |
Vi3*q3 |
Vi4*q4 |
| |
|
2,4 |
0,9 |
0,8 |
0,5 |
4,6 | |
|
1,6 |
0,9 |
1,2 |
0,5 |
4,2 |
Принимая
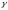 =0,6
=0,6
Получим итоговые данные, для выйгрыша выберем макс. Элемент, для потерь – мин.
|
HL(выйгрыш) |
HL (потеря) |
|
4,02 |
5,22 |
|
3,66 |
4,86 |
Получаем следующий ответ : S*=S1 , V*=4,02 - выигрыш
S*=S2 , V*=4,86 - потеря