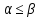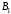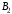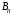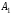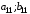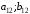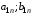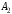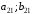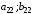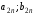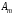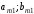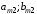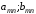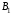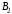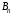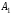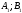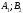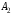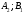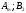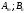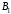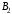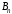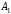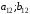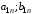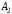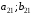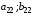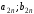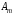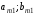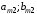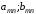1. Задачи теории игр в экономике, финансах и бизнесе.

Теория игр – раздел современной математики, изучающий математические модели принятия решений в т.н. конфликтных ситуациях.

Математическая модель – это математическое описание компонентов и функций, отображающих существенные свойства моделируемого объекта.

Игра – упрощенная, формализованная модель конфликта. Важным отличием игры от реального конфликта является наличие жёстко определённых правил поведения.

Игроки – заинтересованные в конфликте стороны.

Стратегия – любое возможное действие игрока.

Игровая ситуация – результат выбора каждым из игроков своей стратегии.

Выигрыш – то, что обуславливает интерес игроков. (похвала, порицание, приз, штраф).

Три вида игр:

1. Антагонистические

Страховщик и страхователь

На рынке есть страховщик и страхователь. Эта игра антагонистическая, так как выигрыш одного игрока равен проигрышу другого.

Взаимодействие этих сторон можно рассматривать, как игру, потому что есть конфликт интересов. У каждого игрока есть свои стратегии. И они нацелены на максимизацию своего выигрыша, либо минимизацию проигрыша.

2. Игры с природой

Предположим, что инвестор может купить акции одной из 3 компаний. Роль природы исполняет ситуация на фондовом рынке, которая в разные периоды складывается по-разному. Инвестору надлежит принять решение в условиях неопределенности, какой компании отдать предпочтение. На основе этих составляются матрицы выигрышей.

3. Неантагонистические

На рынке есть две фирмы А и В, производят аналогичные товары. Они выбирают объем производимых товаров Q₁ и Q₂.

Если Q=0, то P=A

При этом издержки у них одинаковы = C

Цена зависит от Q: P(Q)=A-Q

Чем больше Q, тем меньше P.

P_k=(A-Q-C)*Q_k

Задача этой модели, найти равновесные Q₁^* и Q₂^*, которые создают ситуацию, которая является равновесием Нэша.

Необходимо найти:

P₁(Q₁;Q₂^*) -> max

P₂(Q₁^*;Q₂) -> max

2. Основные понятия и определения антагонистических игр.

Стратегия – любое возможное действие игрока. Множество стратегий – все возможные стратегии игроков

Игровая ситуация – результат выбора каждым из игроков своей стратегии.

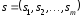
Множество игровых ситуаций – все возможные варианты игровых ситуаций. Образует ситуационное пространство игры.

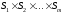
Игра – упрощенная, формализованная модель конфликта. Важным отличием игры от реального конфликта является наличие жёстко определённых правил поведения.

Игроки – заинтересованные в конфликте стороны.

Платежная матрица – матрица, элементами корой являются выигрыши (проигрыши) игрока.

Антагонистическая игра – игра с нулевой суммой, в которой выигрыш одного игрока равен проигрышу другого.

F_A=-F_B , где F – функция выигрыша.

Платежная матрица:

Стратегии игрока A	Стратегии игрока B
			…
			…
			…
…	…	…	…	…
			…

Матрица игровых ситуаций:

Стратегии игрока A	Стратегии игрока B
			…
			…
			…
…	…	…	…	…
			…

3. Взаимосвязь заключается в том, что при игровой ситуации (A₁;B₁) игроки соответственно достигают выигрышей(проигрышей) (a₁₁;b₁₁)

4. 3. Функция выигрыша и матрица выигрышей. Чистые стратегии игроков. Принцип доминирования стратегий. Соотношение между матрицами выигрышей игроков А и В в парной антагонистической игре с нулевой суммой.

Функция выигрыша: 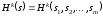_{, k – игроки, s – ситуации.}

Матрица выигрышей:

Стратегии игрока A	Стратегии игрока B
			…
			…
			…
…	…	…	…	…
			…

Чистая стратегия игрока– стратегия, которую выберет игрок с вероятностью = 1.

Доминирование- ситуация, при которой одна из стратегий некоторого игрока дает больший выигрыш, нежели другая, при любых действиях его оппонентов.

Цель принципа доминирования– уменьшить размер матрицы, путем выбрасывания из рассмотрения тех стратегий, которые являются очевидно невыгодными.

4. Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий.

Показатель эффективности: минимальный выигрыш игрока А.

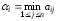
Показатель неэффективности:максимальный проигрыш игрока В.

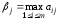
Максиминный принцип:принцип выбора эффективной стратегии, при котором максимизируется показатель эффективности.

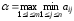
При этом выигрыш 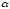– максимин, или нижняя цена игры.

Минимаксный принцип: принцип выбора эффективной стратегии, при котором минимизируется показатель неэффективности.

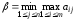
При этом проигрыш 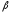- минимакс, или верхняя цена игры.

5. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Соотношение между ними.

Максиминный принцип:принцип выбора эффективной стратегии, при котором максимизируется показатель эффективности.

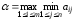
При этом выигрыш 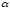– максимин, или нижняя цена игры.

Минимаксный принцип: принцип выбора эффективной стратегии, при котором минимизируется показатель неэффективности.

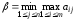
При этом проигрыш 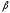- минимакс, или верхняя цена игры.

Соотношение для α и β

Для элементов матрицы A имеют место неравенства

, ,,

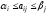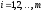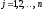и, следовательно, нижняя цена игры не больше её верхней цены в чистых стратегиях:

.

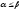6. Критерий решения игры в чистых стратегиях.

Критерий решения игры в чистых стратегиях упирается в критерий существования цены игры в чистых стратегиях.

Свойство: ни одному из игроков А и В, придерживающихся одной из своих оптимальных стратегий невыгодно от нее отклоняться, поскольку в этом случае он не увеличивает свой выигрыш.

Цена игры в чистых стратегиях представляет собой значение выигрыша игрока А, которое он не может увеличить, если игрок В придерживается своей оптимальной стратегии и значение проигрыша игрока В, которое последний не может уменьшить при условии, что игрок А действует по своей оптимальной стратегии.

Теорема: для того, чтобы существовала цена игры в чистых стратегиях, т.е. для того чтобы нижняя цена игры равнялась верхней цене игры, необходимо и достаточно существование у матрицы этой игры седловой точки.

В игре без седловых точек ни у одного из игроков оптимальных стратегий нет. Т.е. задача в чистых стратегияхи меет решение, если сущ. седловая точка.

6. Доказательство утверждения .

Теорема. Для элементов матрицы имеют неравенства 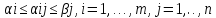и след-ноб нижняя цена игры не больше ее верхней цены в чистых стратегиях: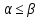

Д-во. По определению 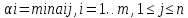показателей эффективности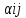стратегийAi и определению 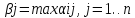показателей неэффективности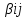стратегийBj игрока В имеем

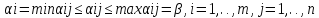, cлед-но 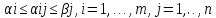доказано

так как доказанное неравенство 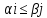справедливо для любыхi=1,..,m, j=1,..n, то оно будет справедливым в частности для номеров i=i₀ и j=j₀ соответственно максиминной и минимаксной стратегией A_i0 и B_j0:

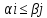
Тогда в силу 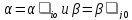получим требуемое неравенство