Прикладна економетрика - Комашко О. В

Комашко О.В.:учбові посібники

1.Черваньов Д.М. Комашко О.В. Економетрика: Курс лекцій, 1998

2.Комашко О.В. Практикум з прогнозування, 2000

3.Комашко О.В. Раєвнєва О.В. Румянцев Н.В. Прикладна економетрика, 2004

Комашко О.В.: переклади

1.Економічне прогнозування: вступ, 1996

2.Економетричний аналіз, 2005

3.Часові ряди для макроекономіки й фінансів, 2005

3

ЗМІСТ

Зміст

Вступ Розділ 1. ЛІНІЙНА РЕГРЕСІЯ

1.1.Проста лінійна регресія

1.2.Множинна лінійна регресія

1.3.Асимптотичні властивості МНК-оцінок.

1.4.Модель лінійної регресії з гетероскедастичними збуреннями

1.5.Модель лінійної регресії з автокорельованими збуреннями

1.6.Метод максимальної правдоподібності.

Розділ 2. МОДЕЛІ З ЛАГОВИМИ ЗМІННИМИ

2.1.Приклади з економічної теорії

2.2.Означення

2.3.Оцінювання моделей з розподіленними лагами 2.4.Обмежене оцінювання скінченних МРЛ 2.5.Моделі з нескінченною довжиною лагів

2.6.Моделі з нескінченою довжиною лагів і економічна теорія 2.7. Оцінювання моделей з нескінченною довжиною лагів.

Розділ 3. СИСТЕМИ СИМУЛЬТАТИВНИХ РЕГРЕСІЙНИХ РІВНЯНЬ Розділ 4. МОДЕЛІ З ОБМЕЖЕНИМИ ЗАЛЕЖНИМИ

ЗМІННИМИ І МОДЕЛІ З ПАНЕЛЬНИМИ ДАНИМИ

4.1.Моделі з обмеженими залежними змінними.

4.1.1.Моделі бінарного вибору. 4.1.2.Моделі з впорядкованим відгуком. 4.1.3.Моделі Тобіт.

4.2. Моделі з панельними даними.

4.2.1.Переваги панельних даних. 4.2.2.Модель з фіксованими ефектами. 4.2.3.Модель з випадковими ефектами. 4.2.4.Фіксовані ефекти чи випадкові ефекти?

Список літератури Додаток1 Статистичні таблиці

Додаток2 Керівництво користувача EViews

5

ВСТУП

Що таке економетрика

Економетрика1 – це галузь економічної теорії, яка вивчає моделі економічних систем у формі, що уможливлює перевірку цих моделей на адекватність засобами математичної статистики. Мета економетрики – здійснювати емпіричну перевірку положень економічної теорії, підтверджуючи чи відхиляючи останні. Цим економетрика відрізняється від математичної економіки, зміст якої полягає виключно у застосуванні математики, і теоретичні положення якої не обов’язково потребують емпіричного підтвердження. Економетрика є результатом синтезу економічної теорії, математичної статистики та економічної статистики. Застосування статистичних методів до аналізу економічних даних має давню історію. Стіглер2 зауважує, що перша «емпірична» крива попиту була опублікована Чарльзом Дейвенентом у 1699 році, а перше сучасне статистичне дослідження попиту було виконано італійським статистиком Родульфо Еніні у 1907 році. Важливим поштовхом до розвитку економетрики було заснування у 1930 році у США Економетричного Товариства і публікація часопису Econometrica (який, до речі, виходить і досі).

Економічні і економетричні моделі

Економічна модель являє собою набір припущень, які приблизно описують поведінку економіки (або сектора економіки). Економетрична модель складається з таких частин: 1). Набір рівнянь поведінки, які виводяться з економічної моделі. Ці рівняння включають деякі змінні, значення яких

1Існує альтернативний правопис – економетрія. Однак, на думку автора, використаний тут варіант є більш вдалим. По-перше, назва «економетрика», на відміну від таких термінів як «геометрія», англомовного походження (хоча і утворена з давньогрецьких коренів):economics – економіка, econometrics –.економетрика. По-друге, зішлемось на авторитет «Орфографічного словника української мови» за редакцією С.І. Головащука і В.М. Русанівського (Київ, «Наукова думка», 1975).

2G.J.Stigler, ’’The Early History of Empirical Studies of Consumer Behavior’’, The Journal of Political Economy, 1954.

6

спостерігаються, а також «збурення», які відтворюють ефект від змінних, не включених до моделі у явному вигляді, та ефект від непередбачуваних подій. 2). Опис імовірнісного розподілу «збурень».

Економетричні моделі мають стохастичний характер. Розглянемо співвідношення між споживанням С та доходом Y у такому вигляді:

С = α + βY + ε, (В.1)

де ε – збурення, або стохастична складова моделі, α і β – невідомі параметри, які можна оцінити за допомогою методів математичної статистики.

Стохастичний характер економетричних моделей дозволяє використовувати теорію статистичних висновків для перевірки цих моделей на адекватність. Перевірка складається з двох етапів: статистичного і економічного. На статистичному етапі ми перевіряємо, чи виконуються вимоги, які накладено на стохастичну складову ε при формулюванні моделі. На економічному етапі ми перевіряємо, чи узгоджуються знайдені оцінки параметрів з положеннями економічної теорії. Наприклад, теорія споживання стерджує, що зі зростанням доходу споживання зростає, але не в такій мірі як доход. Звідси випливає, що модель (В.1) коректна, коли в ній 0 < β < 1.

Таким чином, економетричні методи дозволяють не тільки встановлювати кількісні зв’язки між економічними змінними, але й робити висновки про коректність одержаних моделей.

В першому розділі книзі подано огляд результатів стосовно базової економетричної моделі – моделі лінійної регресії, в тому числі теми, які традиційно не включаються до елементарних курсів економетрики: асимптотична теорія, автокореляція внаслідок неправильної специфікації моделі, спатіальна автокореляція, консистентні в умовах гетероскедастичності оцінки коваріаційної матриці для МНК, метод максимальної правдоподібності включаючи оцінювання коваріаційної матриці і три основні принципи перевірки гіпотез.

7

Розділ 2 присвячений моделям з лаговим змінним. В Розділі розглядаються (більш грунтовно, ніж в елементарних курсах) системи одночасних рівнянь, а в Розділі 4 – моделі з обмеженою залежною змінною і моделі з панельними даними. В Додатку 2. Приведено коротке керівництво користувача програми

Eviews.

7

РОЗДІЛ 1. ЛІНІЙНА РЕГРЕСІЯ

1.1 Проста лінійна регресія

1.1.1. Опис Моделі

Припустимо, що існують дві змінні x i y, де x - незалежна змінна (регресор), y - залежна змінна. Співвідношення між цими змінними позначимо: y = f (x). Будемо розрізняти детерміновані і статистичні співвідношення. При статистичному співвідношенні кожному значенню x відповідає не єдине значення y, але залежну змінну y можливо точно описати у імовірнісних термінах. Припустимо, що функція f(x) лінійна за x, тобто f(x) = α + βx, а співвідношення між x та y є статистичним, а саме

де доданок ε називається збуренням або похибкою і має відомий імовірносний розподіл (тобто є випадковою величиною). В рівнянні (1.1) α + βx є

детермінованим компонентом, збурення ε є випадковим або стохастичним компонентом; α і β називаються регресійними коефіцієнтами або параметрами регресії, які потрібно оцінити на основі даних про x та y.

Нехай ми маємо n пар значень (xi , yi ), i =1, n . Кожну пару будемо називати

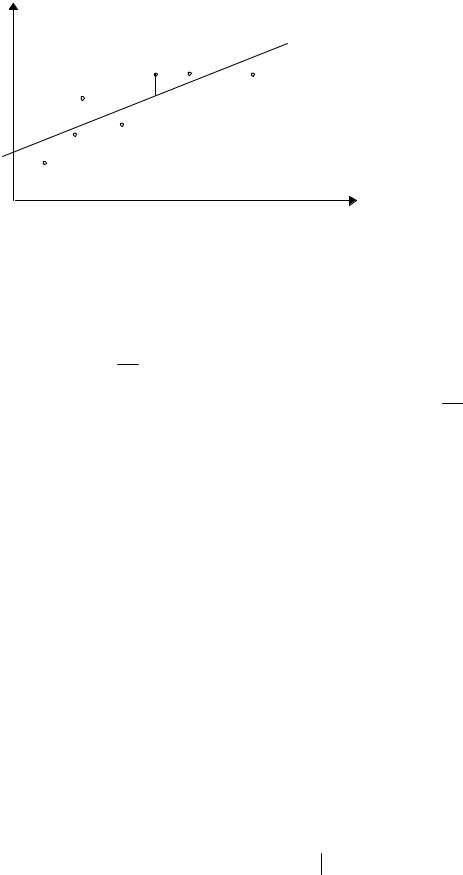
8

y

(xi,yi)

εi

x

Рис.1.1

Наша мета - знайти оцінки невідомих параметрів α та β в рівнянні (1.2) на основі n спостережень x та y. Щоб це зробити ми повинні накласти деякі умови щодо збурень εi.

1.Нульове середнє: Eεi = 0, i =1, n .

2.Рівність дисперсій (гомоскедастичність): Dεi = E ε2i = σ2 = const, i =1, n .

3.Незалежність збурень: εі та εj незалежні при i ≠ j . Зокрема, cov(εi, εj ) = Eεiεj = 0 при i ≠ j .

4.Незалежність збурень та регресора: xi та εj незалежні для всіх i та j. Якщо xi вважаються невипадковими, то дане припущення виконано автоматично.

Вдеяких випадках будемо накладати додаткове припущення (ми будемо вказувати в тексті, для виконнання яких результатів воно необхідно):

5.Нормальність. Збурення εi нормально розподілені для всіх i. Взявши до уваги припущення 1-3, ми можемо сказати, що εi – незалежні нормально розподілені випадкові величини з нульовим математичним сподіванням і однаковими дисперсіями σ2, або εi ~ N (0,σ2 ) .

Отже, модель простої лінійної регресії описується за допомогою рівнянь (1.2), збурення в яких задовольняють припущенням 1 – 5.

Оскільки Eεi = 0, то з рівняння (1.2) маємо E(yi) = E( y xi )α + βxi . Останній

вираз називається популяційною функцією регресії. Таким чином, популяційна функція регресії – функція умовного математичного сподівання. Якщо замінити

9

значення параметрів їх оцінками, одержимо вибіркову функцію регресії. Популяційна регресійна функція дає усереднене, або закономірне значення незалежної змінної, яке відповідає даному значенню незалежної змінної. Збурення можна інтерпретувати як відмінність поведінки залежної змінної від усередненої в кожній конкретній ситуації.

Друге припущення означає,що для кожного спостереження дія випадкових факторів в середньому однакова .

Третє припущення означає, що для кожного спостереження випадкові фактори діють незалежно.

1.1.1. Знаходження оцінок параметрів регресії методом найменших квадратів

Нехай α$ та β$ –деякі оцінки параметрів α та β. Запишемо рівняння вибіркової

регресії y$ = α$ +β$x . Тоді y$i = α$ +β$xi є оцінкою Eyi, побудованою на основі вибіркової регресії. Позначимо через ε$i = yi − y$i різницю між значенням y, яке спостерігалось, і обчисленим з регресії. Оцінки методу найменших квадратів (скорочено – МНК-оцінки) знаходяться з умови мінімізаціїї за всіма можливими значеннями α$ та β$ виразу

Позначимо на координатній площині точки (xi , yi ), i = 1, n і побудуємо графіки

найменших квадрвтів означає пошук прямої, яка знаходиться найближче до даних точок у тому розумінні, що сума квадратів відстаней по вертикалі від даних точок до прямої буде найменшою. Обгрунтування такого вибору методу побудови оцінок полягає в їх оптимальних статистичних властивостях, які сформульовано вище.