Добавил:

Teana Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Таврический Национальный Университет им. В.И. Вернадского

Предмет:

Экономика

Файл:

Прикладна економетрика - Комашко О. В

.pdf

Скачиваний:

Добавлен:

24.05.2014

Размер:

2.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1612 13 14 15 16 > Следующая >>>

Двохетапний метод найменших квадратів, який застосовується для оцінювання систем одночасних рівнянь, є варіантом методу інструментальних змінних, зумовленим конкретним вибором інструментів. Тому зараз немає потреби розглядати коваріаційну матрицю для цих оцінок, оскільки її наведено в розділі, присвяченому системам одночсних рівнянь. Вивір належного набору інструментів в деяких випадках становить складну практичну проблему, але у випадку моделей з автогегресійними лагами завжди можна запропонувати один очевидний розв’язок: в моделі (2.62) використати як інструменти лагові значення X з лагом, більшим, ніж k. Наприклад, в моделі (2.63) інструментами можуть слугувати Xt-1, Xt-2, … .

Для коваріаційної матриці оцінок методу інструментальних змінних також існують аналоги оцінки Неві–Веста на випадок автокорельованих збурень. При виконанні стандартних умов регулярності оцінки методу інструментальних змінних будуть консистентними і асимптотично нормально розподіленими, хоча і не будуть асимптотично ефективними. Однак, їх коректність не потребує припущень про структуру автокореляції збурень (а, отже не залежить від помилок при її визначенні). Цим пояснюється надійність методу.

Крім того, при відомій структурі автокореляції збурень на другому етапі можна застосувати варіант узагальненого методу найменших квадратів, пристосований до наявного типу автокореляції збурень.

На практиці нас частіше цікавлять оцінки параметрів вихідної форми моделі. Отже їх необхідно виразити через параметри авторегресійної форми моделі, а потім в одержані формули підставити знайдені оцінки. Дисперсії можна знайти з використанням формули асимптотичної дисперсії нелінійних функцій від параметрів.

Знаючи конкретну структуру збурень (наприклад ARMA(p,q)), можна застосувати метод максимальної правдоподібності. Вигляд функції правдоподібності у випадку MA-збурень є складним і на практиці можуть виникати проблеми зі збіжністю.

У випадку авторегресійних збурень існує інша дуже проста можливість. Припустимо, що в моделі (2.63) збурення генеруються процесом AR(1). Якщо записати (2.63) для моменту t–1 і з одержаного рівняння виразити εt −1 і

підставити в рівняння (2.63), в якому збурення записано з використанням означення процесу AR(1), то після перепозначення параметрів одержимо рівняння (2.64) з нелінійним обмеженням на параметри. Це обмеження нескладно перевірити. Якщо воно хибне, то це означає що потрібно вибрати модель (2.64). Іншими словами, у вихідній моделі замість геометричного слід використати розподіл лагів Паскаля. Таким чином, у випадку авторегресійних збурень буває можливим звільнитись від автокореляції шляхом включення в авторегресійну форму моделі додаткових лагів, а отже, врешті решт скористатись звичайним методом найменших квадратів в модифікованій моделі.

7.2 Оцінювання у формі рухомого середнього.

Оцінювання здійснюється методом максимальної правдоподібності або нелінійним методом найменших квадратів, а отже ми завжди маємо спиратись на припущення про конкретну структуру автокореляції збурень. Як завжди, три найбільш розповсюджені ситуації: класичні збурення, AR(1)–збурення і МА(1)- збурення. Ми обмежимось розглядом моделі з геометричним розподілом лагів з класичними і AR(1)–збуреннями.

Класичні збурення

Нам буде зручно скористатись записом моделі у вигляді (2.44):

∞
Yt =α + β( 1 − λ )∑λi X t −i	+εt	(2.65).

i=0

Перетворимо (2.65) до такого вигляду:

∞

Yt =α + β( 1 − λ )∑λi X t −i +εt

i=0

=α + β( 1 − λ )( X t + λX t −1 + + λt −1 X 1 ) + β( 1 − λ )λt ( X 0 + λX −1 + ) +εt .

Нехай µ0 = E[Y0 −α ] . Неважко бачити, що третій доданок дорівнює λt µ0 .

Логічно інтерпретувати µ0 як невідомий параметр. Дійсно ми не маємо вибіркової інформації про момент часу 0. Такм чином, модель набуває вигляду

Y =α + β( 1 − λ )X * + λt µ		0	+ε	,
t	t	0	t
де X t* = X t + λX t −1 + + λt −1 X 1				(2.66)

В умовах нормально розподілених збурень логарифмічна функція

правдоподібності для цієї моделі нелінійної регресії має такий вигляд									(2.67)
			LnL(α,β,λ,µ0 ,σε2 ) = −T [ln( 2π ) + lnσε2 ] −			1	2	∑εt2	(2.67)
								T
					2	2σε		t =1
де ε	t	=Y −α − β( 1 − λ )X * − λt µ		0	.
	t	t	t	0

Аналізуючи вигляд функції (2.67), легко зрозуміти, що оцінки максимальної правдоподібності співпадають з оцінками нелінійного методу найменших квадратів. Оцінка дисперсії збурень знаходиться за звичною формулою

σˆ ε2 = 1 ∑T εˆt2 . T t =1

Без припущення про нормальність збурень оцінки нелінійного методу найменших квадратів лишаються консистентними, хоча і можуть виявитись неефективними.

Для фіксованого значення λ оцінки решти параметрів, тобто α, θ=β(1-λ),

та µ0 можна знайти з лінійної регресії Yt відносно константи, X t* і λt . Оскільки

λ лежить між нулем і одиницею, на практиці можна застосувати решітковий пошук. Стандартно спочатку для кожного λ =0,1; 0,2; …;0,9 оцінюють лінійні регресії і в результаті вибирають значення λˆ , яке дає найменшу суму квадратів

залишків. На другому етапі процедура повторюється	в діапазоні [λˆ –0,09;
λˆ +0,09] з кроком 0,01. При необхідності ітерації	можна продовжувати.

Правилом зупинки може бути умова, щоб різниці між двома послідовними

оцінками не перевищували заданий рівень точності. На практиці X t* можна обчислювати з використанням рекурентної формули:

					X 1* = X 1
					X t* = X t	+ λX t*−1	t = 2,...,T .	(2.68)
		Оцінки стандартних похибок можна знайти за допомогою оберненої до
інформаційної матриці. Остання має такий вигляд
I(α,θ,µ0 ,λ,σε2 ) =
			T
			*	*	2
	1		∑t X t	∑t ( X t )
=	1		∑t λt	∑t λt X t*	∑t ( λt )2			(2.69)
=	2		∑t λt	∑t λt X t*	∑t ( λt )2			(2.69)
σε			∑t ∆t	∑t ∆t X t*	∑t ∆t λt	∑t ( ∆t )2
			∑t ∆t	∑t ∆t X t*	∑t ∆t λt	∑t ( ∆t )2
			0	0	0	0	2
			0	0	0	0	T /(σε )
де ∆t		=	∂(θX t* + µ0 λt )
де ∆t		=	∂λ
			∂λ

=θ ∂X t* + µ0 tλt −1 .

∂λ

Вибіркові значення ∂X t* 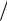∂λ також можна знайти за допомогою рекурентної формули. Використовуючи (2.68), можна показати, що

			∂X 1*	=0 ,
			∂λ
								(2.70)
			∂X 2*	= X 1
			∂λ
і
∂X t*	= λ	∂X t*−1	+ ∂X t*−1 , t = 3,...,T .					(2.71)
∂X t*	= λ	∂λ	+ ∂X t*−1 , t = 3,...,T .					(2.71)
∂λ		∂λ
Нарешті,
			βˆ	=		θˆ	.	(2.72)
			βˆ	=	1	ˆ	.	(2.72)
					1	− λ

Асимтотичну дисперсію останньої оцінки можна оцінити, використовуючи формулу асимтотичної дисперсії нелінійної функції від параметрів:

ˆ ˆ

∂β

D[ β ] ≈

D[θ

] +

D[ λ ] + 2

ˆ Cov[θ ,λ ].

∂θ

∂λ

∂θ

∂λ

Автокорельовані (AR(1)) збурення.

Якщо збурення в (2.66) генеруються процесом AR(1):

εt = ρεt −1 + ut ,

то описаний вище алгоритм можна застосувати до перетвореної моделі:

Yt − ρYt −1 =α( 1 − ρ ) + β( 1 − λ )[ X t* − ρX t* ] + µ0 [ λt − ρλt−1 ] + [ εt − ρεt−1 =ut ]

При заданому значенні ρ в точності повторюєть дії у випадку некорельованих збурень. Для пошуку всього набору параметрів можна організувати двовимірний решітковий пошук λ і ρ.

РОЗДІЛ 3. СИСТЕМИ СИМУЛЬТАТИВНИХ РЕГРЕСІЙНИХ РІВНЯНЬ

3.1.Вступ

Розглянемо наступну функцію попиту на деякий товар:

qid = α0 + α1 pi + εi ,

(3.1)

де qd – обсяг попиту, p – ціна товару, ε – збурення, яке відтворює випадковий зсув функції попиту. З рисунку 5.1 ми бачимо, що зсув функції попиту спричиняє зміни як рівня продаж, так і ціни. Таким чином, в рівнянні (5.1) збурення ε корельоване з регресором p (якщо крива пропозиції не є вертикальною).Має місце наступне твердження: якщо регресори корельовані зі збуреннями, то оцінки методу найменших квадратів будуть не тільки зміщеними, а й неконсистентними1). Отже, потрібно шукати інші методи оцінювання. Економічна теорія підказує, що коли нас цікавить співвідношення між ціною та кількістю, функцію попиту неможливо розглядати ізольовано. До аналізу потрібно включити функцію пропозиції. Розв’язок полягає у сумісному

оцінюванні функцій попиту і пропозиції. Такі моделі відомі як системи симультативних (одночасних) рівнянь.

q	D2	S

	D1

Рис.3.1 Вплив зсуву функції попитуна ціну.

3.2. Класифікація рівнянь і змінних

Проаналізуємо систему рівнянь попиту та пропозиції:

1) Неформально кажучи, це означає, що знайти точні оцінки регресійних коефіціентів неможливо навіть при наявності масиву даних нескінченої довжини. У вітчизняній літературі також вживається «спроможні оцінки». Строге означення див. [ ]

qid =α0		+α1 pi +α2 yi + εi(1)	(3.2)
		+ β1 pi + β2 zi + εi(2)	(3.3)
qis = β0
		,	(3.4)
qd = qs
i	i

i =1,n,

де qd – обсяг попиту, p – ціна товару y – особистий доход, qs – обсяг пропозиції, z – неціновий фактор, який впливає на пропозицію (наприклад, у моделі, яка вивчає попит на сільськогосподарський товар змінна z може бути кількістю опадів). Співвідношення (3.2) – це функція попиту (3.3) – функція пропозиції, (3.4) – тотожність локальної ринкової рівноваги. Системи симультативних рівнянь складаються з рівнянь поведінки та тотожностей. Рівняння (3.2) та (3.3) є рівняннями поведінки, а (3.4) – це тотожність.

Серед змінних, які входять до систем симультативних рівнянь, розрізняють ендогенні і екзогенні. Значення ендогенних змінних визначаються в моделі, а значення екзогенних змінних – за рамками моделі. Ендогенні змінні також називають сумісно визначеними, а екзогенні змінні – предетермінованими (наперед визначеними). В групу предетермінованих змінних також включають лагові значення ендогенних змінних (значення ендогенних змінних в попередні моменти часу). Ендогенні змінні корельовані зі збуреннями в рівняннях, а екзогенні – некорельовані. В цьому останні подібні до незалежних змінних в звичайних регресійних моделях.

В системі (3.2) – (3.4) змінні p, qd та qs є ендогенними, а y і z – екзогенними. Систетеми симультативних рівнянь повинні задовольняти наступній умові повноти: кількість рівнянь має співпадати з кількістю ендогенних змінних в системі.

3.3. Структурний і зведений вигляд систем симультативних рівнянь

Внаслідок тотожності локальної ринкової рівноваги систему (3.2) – (3.4) можна переписати у такому вигляді:

qi =α0qi = β0

i =1,n,

+α1 pi +α2 yi + εi(1)

+β1 pi + β2 zi + εi(2) ,

(3.5)

(3.6)

де q – рівноважна кількість (об’єм продаж або рівень споживання). Змінні p та q є ендогенними, а y і z – екзогенними. Системи (5.2) – (5.4) та (5.5), (5.6) записано у структурному вигляді. У структурному вигляді системи симультативних рівняь кожне рівняння відображає певний елемент структури економічної системи, що роглядається, і має економічну інтерпретацію. Крім стрктурного нам знадобиться зведений вигляд систем симультативних рівнянь.

У зведеному вигляді в кожному рівнянні зліва стоїть ендогенна змінна, а справа

– лише екзогенні змінні.

Трансформуємо систему (3.5), (3.6) до зведеного вигляду. Для простоти опустимо індекс i. Віднімемо почленно рівняння (3.5) від рівняння (3.6):

0 = α0 – β0+(α1 – β1)p + α2y – β2z + ε(1) – ε(2),

звідки

p =

− β

ε(1) − ε(2)

(3.7)

β1 − α1

α1 − β1

β1 − α1

Від рівняння (3.5), помноженого на β1, віднімемо (5.6), помноженене на α1:

q(β1–α1) = α0β1 – α1β0 + α2β0y – α0β2z + β1ε(1) – α1ε(2),

звідки

	α	0	β	1	− α	β	0		α	2	β	1	y		β	2	α	z		β	ε(1) − α	ε(2)
q =		0		1	1		0	+		2		1		+		2	1		+	1	1		.	(3.8)
q =		β1 − α1						+	β1 − α1					+	α1 − β1				+				.	(3.8)
		β1 − α1							β1 − α1						α1 − β1						β1 − α1

Формули (3.7) і (3.8) коректні за умови β1 ≠ α1. Останнє співвідношення є гарантованим з економічних міркувань, оскільки α1 і β1 повинні мати різни знаки як коефіціенти при ціні у функціях попиту та пропозиції. Зробимо наступні позначення:

π11

α0

− β0

− α

π12

α2

− α

π13

β2

α1

− β1

π21 =

α0β1 − α1β0

β1 − α1

α2β1

− α

π23

β2α1

− β

υ(1) =

ε(1)

− ε(2)

β1

− α1

υ(2) = β1ε(1) − α1ε(2) .

β1 − α1

Враховуючи введені позначення, маємо:

	+π12 y +π13 z +υ	(1)		(3.9)
p =π11	+π12 y +π13 z +υ			(3.9)
			(1)

p =π21 +π22 y +π23 z +υ				(3.10)
p =π21 +π22 y +π23 z +υ				(3.10)

Рівняння (3.9) та (3.10) є рівняннями зведеного вигляду.

Зауважимо, що оскільки у рівняннях зведеного вигляду справа стоять лише екзогенні змінні, некорельовані зі збуреннями, то ці рівняння коректно оцінювати за допомогою звичайного методу найменших квадратів.

3.4. Проблема ідентифікації

3.4.1.Ідентифікація через зведений вигляд

Наша остаточна мета в цьому розділі – навчитись знаходити консистентні оцінки коефіціентів рівнянь структурного вигляду. Виявляється, що такі оцінки не завжди існують. Концепція ідентифікованості пов’язана, грубо кажучи, з

можливістю консистентного оцінювання. В основу класифікації систем рівнянь з точки зору ідентифікованості покладено можливість виразити коефіціенти рівнянь структурного вигляду через коефіціенти рівнянь зведеного вигляду. Попередньо зауважимо, що в тій самій системі деякі рівняння можуть бути ідентифікованими, а деякі – ні. Рівняння називається строго ідентифікованим, якщо його коефіціенти можна однозначно виразити через коефіціенти рівнянь зведеного вигляду. Якщо існує більш ніж один розв’язок, то рівняння є

надідентифікованим. Рівняння є неідентифікованим, якщо його коефіцієнти неможливо виразити через коефіціенти рівнянь зведеного вигляду.

Дослідимо на ідентифікованість систему (3.5), (3.6). Виразимо α0, α1, α2, β0,

β1, β2 через π11, π12, π13, π21, π22, π23. Маємо:

					β	=		π22	,
					β	=		π	,
					1			π
								12
					α		=	π23		,
					α		=	π		,
					1			π
								13
α		= π (β − α					) = π				π	22	−	π		23
α	2	= π (β − α				1	) = π					22	−	π		23	,
	2	12	1			1		12			π			π		13
												12				13
β		= π (α			− β ) = π						π	23	−	π	22
β	2	= π (α		1	− β ) = π						π	23	−		22		,
	2	13		1	1			13			π	13		π
												13			12

α0 = π11 − α1π21 = π11 − π21 π23 , π13

β0 = π11 − β1π21 = π11 − π21 π22 . π12

Ми бачимо, що обидва рівняння є строго ідентифікованими.

3.4.2. Порядкова та рангова умова ідентифікованості

Перевірка рівнянь системи на ідентифікованість здійснюється за допомогою порядкової та рангової умов. Сформулюємо лише порядкову умову. Спочатку нам потрібно підрахувати кількість ендогених та екзогенних змінних системи в цілому і кількість ендогенних і екзогенних змінних, що входять в дане рівняння. Позначимо через kj кількість ендогенних змін, які входять до j-го

рівняння системи, m*j – кількість екзогенних змін, які не входять до j-того рівняння. Рівняння строго ідентифіковане, якщо kj = m*j . Рівняння надідентифіковане, якщо kj < m*j . Рівняння неідентифіковане, якщо kj > m*j .

Наведемо наступний простий наслідок з рангової умови ідентифікації. Якщо в кожному рівнянні системи є екзогенна змінна, яка не входить до жодного з решти рівнянь, то кожне з рівнянь системи є ідентифікованим.

3.5. Методи оцінювання систем симультативних рівнянь

3.5.1. Непрямий метод найменших квадратів

Розберемо цей метод на прикладі системи (5.5), (5.6). Як ми зазначали в кінці параграфа 5.2, коефіціенти рівняннь зведеного вигляду можна оцінювати за допомогою звичайного МНК. Позначимо через π$ij оцінку методу найменших

квадратів коефіціента πij, i = 1, 2; j = 1, 2, 3. Щоб знайти оцінки непрямого методу найменших квадратів коефіціентів рівнянь структурного вигляду достатньо в формулах, які виражають коефіціенти рівнянь структурного вигляду через коефіціенти рівнянь зведеного вигляду, замінити останні іх оцінками:

β$1 = π$22 , π$12

α$1 = π$23 π$13

і так далі.

Зауважимо, що за допомогою непрямого методу найменших квадратів можна оцінювати лише строго ідентифіковані рівняння.

3.5.2 Двоетапний метод найменших квадратів

Цей метод можна застосовувати для оцінки строго та надідентифікованих рівнянь. На першому етапі за допомогою звичайного методу найменших квадратів оцінюємо регресії кожної ендогенної змінної відносно набору всіх

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1612 13 14 15 16 > Следующая >>>

Соседние файлы в предмете Экономика