Прикладна економетрика - Комашко О. В
.pdf11
Нехай Sxx> 0. Запишемо розв’язок системи нормальних рівнянь відносно β$ за правилом Крамера:
|
n |
n |
n |
|
|
n∑xi yi − ∑xi ∑ yi |
|
||
β$ = |
i=1 |
i=1 |
i=1 |
(1.6). |
n |
n |
|
||
|
n∑xi2 |
− (∑xi )2 |
|
|
|
i=1 |
i=1 |
|
|
Розділимо чисельник і знаменник виразу (1.6) на n. Враховуючи уведені
позначення, остаточно одержимо: β$ = |
Sxy |
. Розділимо перше нормальне |
Sxx |
рівняння (1.4) почленно на n. Маємо: y = α$ +β$x . Надалі будемо позначати МНК-оцінки параметрів α та β латинськими літерами a та b. Отже, МНКоцінки параметрів моделі простої лінійної регресії знаходяться за фомулами:
b = |
Sxy |
|
(1.7) |
Sxx |
|||
a = y − bx |
|
||
|
|
|
|
Якщо обчислити матрицю других похідних для Q, то можна побачити, що ця матриця додатньо визначена, отже значення (1.7) дійсно мінімізують (1.3).
Рівняння вибіркої регресії приймає вигляд
y$ = a + bx . |
(1.8) |
З першого нормального рівняння випливає, що графік вибіркової регресійної прямої (1.8) проходить через точку середеніх значень залежної та незалежної змінних. Рівняння (1.8) дає нам уявлення про характер залежності (точніше детермінованої її частини) між змінними x та y.
12
1.1.3.Властивості залишків методу найменших квадратів
Позначимо через ei , i =1, n різниці між фактичними та теретичними, тобто обчисленими з рівняння вибіркої регресії (1.8) значеннями залежної змінної:
ei = yi − y$i = yi −(a + bxi ) |
(1.9) |
– залишки методу найменших квадратів (аналогічно тому, як ми домовились щодо позначень оцінок методом найменших квадратів, замість загального позначення залишків ε$i , для залишків методу найменших квадратів будемо використовувати літеру e). Залишки можна вважати вибірковими, або емпіричними аналогами збурень. З урахуванням уведених позначень перше нормальне рівняння запишеться у вигляді
n |
|
∑ei = 0 |
(1.10). |
i=1
Отже, сума залишків методу найменших квадратів дорівнює нулю. Друге нормальне рівняння прийме вигляд
∑n |
x i e i = 0 |
(1.11). |
i =1 |
|
|
Або, якщо позначити через x вектор значень незажної змінної, а через e вектор залишків:
x1 |
|
|
e1 |
|
|
|||
x |
|
|
, |
e |
|
, |
||
x = |
|
2 |
|
e = |
2 |
|
||
|
... |
|
|
... |
|
|||
x3 |
|
|
en |
|
||||
то (x,e) = 0 . Тобто, залишки методу найменших квадратів ортогональні до
регресора.
|
|
|
|
|
|
|
|
|
13 |
1.1.4.Розклад дисперсії залежної змінної. Коефіціент |
|||||||||
|
детермінації |
|
|
|
|
|
|
||
З рівнянь (1.8) та (1.9) випливає, що |
|
|
|
|
|
|
|
|
|
|
yi = a + bxi + ei ,i = |
|
|
|
|
(1.12) |
|||
|
1, n |
||||||||
Запишемо другу з формул (1.7) у вигляді |
|
|
|
|
|
|
|
|
|
|
y = a + bx |
|
|
|
|
|
(1.13) |
||
Від кожного з рівняннь (1.12) віднімемо рівняння (1.13): |
|
||||||||
yi |
− y = b(xi − x ) +ei ,i = |
|
|
(1.14) |
|||||
1, n |
|||||||||
Кожне з рівнянь (1.14) піднесемо до квадрату і додамо почленно. Маємо |
|||||||||
n |
n |
n |
|
|
|
n |
n |
||
∑( yi − y)2 = S yy = b2 |
∑(xi − x )2 |
+ ∑ei2 |
+ 2b∑xiei − 2bx ∑ei = |
||||||
i =1 |
i=1 |
i =1 |
|
|
|
i =1 |
i =1 |
||
|
|
n |
|
|
|
|
|
|
|
|
= b2Sxx + ∑ei2 , |
(1.15) |
|||||||
|
|
i =1 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
∑ y$i |
|
|
|
|
|
|
|
внаслідок (1.10) та (1.11). Позначимо y$ = |
i=1 |
. З (1.10) випливає, що y = y$ . |
|||||||
n
Тому
yi − y = ( yi − y$i ) +( y$i − y) = ei + y$i − y$ .
Порівнюючи останнє рівняння з (1.14), бачимо, що
14
b(xi − x ) = y$i − y$ ,
отже
n
b2 Sxx = ∑( y$i − y$)2 .
i=1
Уведемо такі позначення:
n
TSS = S yy = ∑( yi − y)2 – загальна сума квадратів,
i=1
n
ESS = b2Sxx = ∑( y$i − y$)2 – пояснена сума квадратів, або сума квадратів
i =1
регресії
n
RSS = ∑ei2 –сума квадратів залишків.
i=1
Загальна сума квадратів пропорційна до вибіркової дисперсії залежної змінної. Пояснена сума квадратів пропорційна до вибіркової дисперсії незалежної змінної. Отже, дисперсія залежної змінної складається з двох частин. Перша виникає завдяки розкиду значень незалежної змінної. Тобто, ця частина пояснюється за рахунок моделі (звідси і назва – пояснена сума квадратів). Друга частина – сума квадратів залишків – виникає внаслідок збурень і не пояснюється за рахунок моделі. Записавши співвідношення (1.15) з урахуванням уведених позначень, одержимо формулу розкладу дисперсії:
TSS = ESS + RSS |
(1.16). |
Коефіціент детермінаціїї R2 визначається як частка поясненої і загальної сум квадратів
|
|
|
|
15 |
|
|
|
|
|
|
|
R2 = |
ESS |
=1− |
RSS |
(1.17). |
|
TSS |
TSS |
||||
|
|
|
|||
|
|
|
|
|
Для обчислення коефіціента детермінації можна користуватись такими формулами
R |
2 |
|
b2 S |
xx |
|
bSxy |
|
Sxy2 |
|
|
|
= |
|
= |
|
= |
|
. |
(1.17а) |
||
|
S yy |
S yy |
|
|||||||
|
|
|
|
|
Sxx S yy |
|
||||
Коефіціент детермінації є частиною дисперсії залежної змінної , яка пояснюється за рахунок моделі, або, іншими словами, завдяки мінливості незалежної змінної. Коефіціент детермінації є мірою тісноти саме лінійного
зв′язку між x та y. Коефіціент детермінації завжди знаходиться в межах від нуля до одиниці. Чим ближче R2 до 1, тим точніше x пояснює y. Якщо R2 = 1, це означає, що всі значення x та y лежать на одній прямій. Якщо R2 = 0 ,то лінія регресії – горизонтальна пряма; це означає відсутність (лінійного) зв′язку між змінними. Коефіціент детермінації є мірою згоди регресії. Проілюструємо сказане графічно. На Рис. 1.2 зображено три набори даних по 100 спостережень в кожному, утворені за допомогою датчика випадкових чисел, разом з вибірковими регресійними прямими, знайденими за домогою методу найменших квадратів. В кожному випадку розраховано коефіцієнт детермінації.
6 |
|
|
|
10 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.5 |
|
|
|
8 |
|
|
|
3.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
6 |
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
4.5 |
|
|
|
2 |
|
|
|
2.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5 |
3 |
3.5 |
4 |
2.5 |
3 |
3.5 |
4 |
2.5 |
3 |
3.5 |
4 |
а) тісний зв’язок : |
б) відсутність зв’язку: |
в) відсутність зв’язку: |
R2 = 0.970261 |
R2 = 0.000771756 |
R2 = 0.0000665667 |
Рис 1.2. |
|
|
16
У випадку, зображеному на Рис. 1.2.а) має місце досить тісний лінійний зв’язок між змінними. У випадках б) та в) лінійний зв’язок практично відсутній. Однак між цими двома ситуаціями існує істотна різниця. На Рис. 1.2 б),
очевидно, відсутній будь-який зв’язок між змінними, тоді як точки на Рис. 1.2.в) розташовані навколо деякої параболи.
1.1.5.Статистичні властивості оцінок методу найменших квадратів
Оцінки методу найменших квадратів є незміщеними1) :
Eb = β, Ea = α .
Дисперсії та коваріація оцінок методу найменших квадратів обчислюються за наступними формулами:
Da = σ |
2 |
|
1 |
+ |
|
x 2 |
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
||||||||
|
σ2 |
n |
|
|
|
S xx |
|
||||
Db = |
|
|
|
|
|
|
|
|
(1.18) |
||
S xx |
|
|
|
|
|
|
|||||
|
|
|
|
− x |
|
||||||
cov(a, b) = σ |
2 |
||||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
S xx |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Наведені формули не можна використовувати для перевірки гіпотез та інтервального оцінювання, оскільки до них входить невідомий параметр – дисперсія збурень σ2 . Отже, нам потрібно вміти знаходити її оцінку. Має місце наступний результат: статистика
1) Оцінка θ$ параметра θ називається незміщеною, якщо Eθθ$ = θ .
17
σ$2 = RSS n − 2
є незміщеною оцінкою σ2. Якщо збурення нормально розподілені, то a та b також нормально розподілені. Величина
n
RSS = (n − 2)∑i =1 ei2
σ2 σ2
має χ2 - розподіл з n - 2 ступенями свободи. Більше того, випадкова величина RSS не залежить від a та b.
Далі ми будемо припускати, що збурення нормально розподілені. Як відомо,
якщо випадкові величини ξ1~N(0,1), ξ2~ χ2p незалежні2) , то
t = |
ξ1 |
p |
= |
|
ξ2 |
|
|
|
стандарний нормальний розподіл |
|
|||||||
= незалежний χ2 −розподіл, що ділиться на свою кількість ступенів свободи |
||||||||||
має розподіл Стьюдента з p ступенями свободи. |
|
|||||||||
Оскільки |
b ~ N(β,σ2 |
|
) , то |
b −β |
має |
стандартний нормальний |
||||
|
|
|
Sxx |
σ |
2 |
Sxx |
|
|
||
|
|
|
|
|
|
|
|
|
||
розподіл. Крім того, |
|
RSS |
|
~ χ2n−2 і |
ці |
випадкові |
величини незалежні. Отже, |
|||
|
σ2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
частка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b −β |
|
|
RSS |
= |
b −β |
|
|
|
|
σ2 Sxx |
(n − 2)σ2 |
|
σ$2 Sxx |
|||
2) Знак «~» читається: (випадкова величина) «має розподіл».
18
має розподіл Стьюдента з n - 2 ступенями свободи. Величина σ$2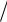
Sxx є оцінкою
дисперсії b, а σ$2 Sxx – оцінкою середньоквадратичного відхилення, або,
коротко, стандартною похибкою оцінки b. Уведемо позначення SE(b) =
σ$2 Sxx (від англійського standard error - стандартна похибка). Маємо
|
b − β |
~ tn−2 |
(1.19) |
|
SE(b) |
||
|
|
|
|
|
|
|
|
1.1.6.Статистичні висновки в моделі простої лінійної регресії
Перевірка гіпотез про коефіцієнт нахилу регресії
Стандартною процедурою є перевірка гіпотези про те, що коефіцієнт нахилу регресійної прямої β дорівнює нулю. Прийняття цієї гіпотези означає, що незалежна змінна не має впливу на залежну в рамках лінійної моделі. Не виключено, що насправді між змінними існує залежність, але виражена іншою функціональною формою. Статистика для перевірки гіпотези має вигляд
t = |
b |
(1.20) |
|
SE(b) |
|||
|
|
Значення цієї t-статистики, як правило, автоматично підрахо-вуються в комп’ютерних програмах з регресійного аналізу. Для перевірки гіпотези H0: β = β0 використовують наступну статистику
t = |
b − β0 |
(1.21) |
SE(b) |
За вибраним рівнем значущості α в таблиці розподілу Стьюдента з n-2
ступенями свободи знаходимо критичне значення tкр. Якщо |t| < tкр, то гіпотеза
H0 приймається. Якщо |t| ≥ tкр, то гіпотеза H0 відхиляється.
19
Інтервальне оцінювання
Інтервальна оцінка параметра β з рівнем довіри 1-α (не плутати з постійним доданком у регресії) знаходиться за наступною формулою:
(b − SE(b) tкр;b + SE(b) tкр ) , |
(1.22) |
де значення tкр знаходиться за вибраним α в таблиці розподілу Стьюдента з n-2 ступенями свободи.
Перевірка значущості регресії
Значущість регресії означає, що незалежні змінні впливають на залежну змінну. Для простої лінійної регресіі це еквівалентно тому, що коефіцієнт нахилу не дорівнює нулю (тобто коли гіпотеза про рівність β нулю
відхиляється) . Якщо b = 0, то R2 = 0. Тому логічно будувати критерій, який грунтується на значенні коефіцієнта детермінації. Дійсно, можна показати, що
R2
F = |
1 |
~ F |
(1.23) |
|
|||
|
1 − R2 |
1,n−2 |
|
|
|
|
n − 2
коли β = 0, де через F1,n–2 позначено розподіл Фішера з 1, n–2 ступенями свободи. За вибраним рівнем значущості α в таблиці розподілу Фішера з 1, n-2
ступенями свободи знаходимо критичне значення F кр. Якщо |F|<Fкр, то гіпотеза приймається. Якщо |F|≥Fкр, то гіпотеза відхиляється. У випадку простої регресії застосування F-критерія (1.23) не дає нової інформації порівняно з t-критерієм
(1.20), оскільки t 2 = F 2 і t 2 |
= F 2 |
. Але це не так у випадку множинної регресії, |
кр |
кр |
|
що ми побачимо пізніше. |
|
|
20
1.1.7. Прогнозування за допомогою простої лінійної регресії
Припустимо, ми хочемо одержати інформацію про можливі значення залежної змінної y0 за умови, що незалежна змінна x приймає деяке значення x0. Внаслідок (1.1) y0 = α + βx0 + ε0 . Точковий прогноз знаходиться за формулою
y$0 = a + bx0 |
(1.24). |
Оскільки Ea = α і Eb = β, то Ey$0 = E(a + bx0 ) = α + βx0 = Ey0 . Отже, прогноз
(1.24) є незміщеним. Дисперсія Dy$0 прогнозу (1.24) дорівнює |
|
||||||||
Dy$ |
|
= σ2 |
1 + |
1 |
+ |
(x0 |
− x )2 |
(1.25). |
|
0 |
|
|
|
|
|||||
|
|
|
n |
|
|
|
|
||
|
|
|
|
|
|
Sxx |
|
||
Для того, щоб (1.25) можна було б використовувати для інтервального оцінювання залишилось замінити дисперсію збурень на її оцінку. Позначимо
SE( y$ |
0 |
) = |
σ$ |
2 |
1 + 1 |
+ (x0 |
− x )2 |
– |
(1.26) |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
Sxx |
|
|
|
стандартна похибка прогнозу. Інтервальний прогноз з рівнем довіри
1-α знаходиться за наступною формулою:
( y$0 − s.e.( y$0 ) tкр; y$0 + s.e.( y$0 ) tкр ) ,
де y$0 – точковий прогноз (1.24), а значення tкр знаходиться за вибраним α в
таблиці розподілу Стьюдента з n-2 ступенями свободи.
1.1.8.Приклад