
Прикладна економетрика - Комашко О. В
.pdfВ результаті підстановки (2.36) до (2.35) одержуємо
∞ |
|
|
|
Yt =α + β0 ∑λi X t−i |
+εt |
(2.37) |
|
i−0 |
|
|
|
Запишемо (2.37) для моменту t −1: |
|
|
|
∞ |
|
|
|
Yt−1 =α + β0 ∑λi X t−1−i |
+ εt−1 |
(2.38) |
|
i−0 |
|
|
|
Помножимо (2.38) на λ і віднімемо від (2.37) |
|
||
Yt − λYt =α( 1 − λ ) + β0 X t + εt |
− λεt −1 |
(2.39) |
|
Перенесемо λYt в праву частину рівняння: |
|
||
Yt =α0 + β0 X t |
+ λYt −1 +υt , |
(2.40) |
|
де α0 =α( 1 − λ ); υt = εt − λεt −1
Оскльки модель (2.40) містить лагове значення Yt −1 залежної змінної, вона
відноситься до класу |
авторегресійних |
або |
динамічних моделей. |
Збурення |
||||||||||||||||||
υt =εt − λεt −1 є процесом рухомого середнього першого порядку (МА(1)). |
||||||||||||||||||||||
Обчислимо характеристики впливу, введені в параграфі 2.3. |
|
|||||||||||||||||||||
Середній лаг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
∞ |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑iβi |
|
β0 ∑iλi |
|
λ /( 1 − λ ) |
2 |
|
|
λ |
|
|
|||||||||
|
w = |
i=0 |
|
= |
|
i=0 |
= |
|
= |
(2.41) |
||||||||||||
|
∞ |
|
|
∞ |
1 /( 1 − λ ) |
1 − λ |
||||||||||||||||
|
|
|
∑βi |
|
|
β0 ∑λi |
|
|
|
|
||||||||||||
|
|
|
i=0 |
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Медіаний лаг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
w−1 |
|
w−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
medialag = min w : = min w := |
|
β0 ∑λi |
= |
∑βi |
|
= |
( 1 |
− λ |
w |
) /( 1 − λ ) |
=1 − λw =0,5 |
|||||||||||
|
i=o |
|
i=0 |
|
|
|||||||||||||||||
∞1 |
∞ |
|
|
|
|
|
|
|
|
|||||||||||||
w−1 |
|
|
|
|
|
|
|
|
|
1 /( 1 − λ ) |
|
|||||||||||
∑wi |
|
|
|
|
β0 ∑λ |
|
∑βi |
|
|
|
|
|
||||||||||
i =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=o |
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Тобто середній лаг визначається з рівняння |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 − λw =0,5 , |
|
|
|
|
|
|
|
|
|
||||||
|
або α w |
= 0,5, звідки median lag = |
ln0,5 |
|
(2.42) |
|||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lnλ |
|
|||
Миттєвий мультіплікатор дорівнює β0 .
Рівноважний мультіплікатор:
∞ |
|
∞ |
|
1 |
|
|
|
β = ∑βi |
= β |
0 ∑λi |
= β0 ( |
) |
(2.43) |
||
1 − λ |
|||||||
i=0 |
|
i=0 |
|
|
|
Якщо записати замість (2.36)
|
∞ |
|
|
|
Yt =α |
0 + ∑βi X t−i |
+ εt |
, |
|
|
i=0 |
|
|
|
|
|
|
де βi = β( 1 − λ )λi |
(2.44) |
то β інтерпретується як рівноважний мультіплікатор. Тому деякі автори
віддають перевагу останньому формулюванню моделі.
2.5.2.Розподіл лагів Паскаля |
|
|
|
|
||||
Дана модель запропонована Солоу. |
|
|
|
|
||||
Коефіцієнти βi в основному рівнявнні (2.35) визначаються так |
|
|||||||
|
|
|
|
βi = βwi для i = |
|
, |
(2.45) |
|
|
|
|
0,∞ |
|||||
де |
|
|
|
|
|
|
|
|
w |
= ci |
|
( 1 − λ )r λi = |
( i + r −1 )! |
( 1 − λ )r λi |
(2.46) |
||
+r −1 |
|
|||||||
i |
i |
|
i!( r −1 )! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Де r - натуральне число, 0 < λ <1.
На відміну від моделі з геометричним розподілом лагів, в якій
коефіцієнти |
βi монотоно |
|
спадають, |
|
тепер коефіцієнти |
наслідують схемі |
||||||||||||||||||||||||||||||||
«оберненого V». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для того, щоб записати модель з розподілом лагів Паскаля підставимо |
||||||||||||||||||||||||||||||||||||||
(2.45) до (2.35) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Y =α + β( 1 − λ )r [ X |
|
+ rλX |
|
|
|
+ |
r( r + 1 ) |
λ2 X |
|
|
|
+ ...] + ε |
|
(2.47) |
||||||||||||||||||||||||
t |
t −1 |
|
|
|
|
|
|
|
t −2 |
t |
||||||||||||||||||||||||||||
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В моделі (2.47) невідомі параментри α,β,λ,r . Зауважимо, що модель з |
||||||||||||||||||||||||||||||||||||||
геометрично розподіленими лагами є частковим випадком (2.47) при r = 1. |
||||||||||||||||||||||||||||||||||||||
Вплив |
параметра |
r |
|
|
на |
характер розподілу лагів проілюстровано на |
||||||||||||||||||||||||||||||||
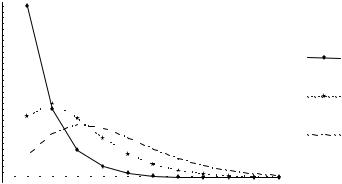
рисунку 2.2, на якому зображено графік вагів для λ = 0,4 і r |
= 1,3,5 відповідно. |
|||||||||||||||||||||||||||||||||||||
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 1 |
|
||||
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 3 |
|
|||
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 5 |
|
|||
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
6 |
|
|
|
|
8 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рисунок 2.1
Модель з розподілом лагів Паскаля також можна записати у вигляді авторегресійної моделі.
Згадаймо, що однію з основних переваг моделей з розподіленими лагами є можливість досліджувати розподіл в часі реакції залежної змінної на зміну визначальних факторів. Причиною уведення структур розподілів лагів, розглянутих нами, були такі недоліки моделей з необмеженими лагами як мультиколінеарність і необхідність визначення максимальної довжини лагу (надійність статистичних методів визначення максимальної довжини лагу також зменшується внаслідок мультиколінеарності). Проблема максимальної довжини лагу стосується і моделей з поліномільно розподіленими лагами. Моделі з геометричним розподілом лагів спираються на припущення, що величина реакції з самого початку монотонно спадає в часі. На практиці таке припущення виконується далеко не завжди. Наведемо такий тривіальний приклад. Припустимо, що ми використовуємо щомісячні дані, а максимальна реакція проявляє себе через 4 місяці. Зрозуміло, що в такому випадку найбільший коефіцієнт має бути при Yt-4. Таким чином, на нашу думку розподіл лагів Паскаля є найбільш гнучким засобом моделювання серед розглянутих нами, хоча, як ми побачимо у параграфі 6, в деяких випадках вигляд розподілу лагів можна вивести з економічних міркувань. У наступному підпараграфі ми розглянемо подальше узагальнення розподілу лагів Паскаля.
2.5.3.Оператор лагу і моделі з раціонально розподіленими лагами
Оператор лагу L вводиться для спрощення викладок. Він визначається за допомогою співвідношення
LX t = X t −1
Наведемо деякі корисні алгебраїчні властивості оператора лагу
L( LX t ) = L2 X t = X t −2 , Lp X t = X t − p , Lp ( Lp X t ) = Lp +q X t = X t − p −q , Lo X t = X t , Lp ( aX t ) = aLp X t = aX t −2
де a - костанта.
З використанням оператора лагу основна модель (2.35) набуде вигдяду
∞ |
|
∞ |
|
|
|
Yt =α + ∑βi X t −i |
+ ε |
=α + ∑βi Li X t |
+εt =α + β( L )X t |
+ εt |
(2.48) |
i =0 |
|
i =0 |
|
|
|
∞ |
|
|
|
|
|
де β( L ) = ∑βi Li |
= β0 + β1 L + β2 L2 + β3 L3 + ... |
|
(2.49) |
||
i =0
поліном відносно L .
∞
Вираз ∑βi Li як збіжний степеневий ряд можна проінтерпретувати як
i=0
розклад в ряд Тейлора функції β( L ) . Йоргенсон в запропонував розглянути моделі, в яких функція β( L ) є раціональною, тобто
|
|
|
|
β( L ) = |
γ( L ) |
= |
γ0 |
+γ1 L + γ 2 L2 |
+ ... +γ p Lp |
|
(2.50) |
||
|
|
|
|
δ( L ) |
δ0 |
+δ1 L +δ2 L2 |
+ ... + δq Lq |
||||||
|
|
|
|
|
|
|
|
|
|||||
|
Підставимо (2.50)до (2.48), поклавши δ0 |
= 1 : |
|
|
|||||||||
Y =α + |
γ( L ) |
X |
|
+ ε |
|
|
|
|
|
|
|
|
|
|
t |
t |
|
|
|
|
|
|
|
||||
t |
δ( L ) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
Помножимо обидві частини останньої рівності на δ( L ): |
|
|||||||||||
δ( L )Yt =αδ( L ) +γ( L )X t +δ( L )εt , |
|
|
|
||||||||||
звідки |
|
|
|
|
|
|
|
|
|
|
|||
|
|
Yt =α0 |
+γ0 X t |
+γ1 X t −1 |
+ ...+γ p X t − p −δ1Yt −1 ... −δqYt −q +υt |
(2.51) |
|||||||
де α0 |
=αδ( L ) =α( 1 +δ1 + ... +δq ) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
і υt =δ( L )εt =εt +δ1εt −1 + ... +δqεt −q |
(2.52) |
|||||
Рівняння (2.51) задає модель з раціонально розподіленними лагами в авторегресійній формі. Ця модель узагальнює дві розглянуті раніше моделі. Поклавши в (2.51) γ( L ) =γ 0 і δ( L ) = 1 −λL одержуємо модель з геометрично розподіленими лагами. Модель з розподілом лагів Паскаля одержуємо, якщо
γ( L ) =γ( 1 − λL )r−1 і δ( L ) = ( 1 −λL )r .
2.6.Моделі з нескінченою довжиною лагів і економічна теорія
Всі моделі з нескінченою довжиною лагів розглягуті вище, вдалось привести до авторегресіної форми.
Відповідні перетворення мали технічний характер, оскільки здійснювались з метою позбутися від нескінченної кількості невідомих параменрів в моделях. В цьому розділі ми розглянемо приклади з економічної теорії, які безпосередньо призводять до авторегресійної форми моделей з розподіленними лагами.
2.6.1.Модель часткового пристосування
Цю модель запропонував Марк Нерль. Він припустив, що поточний
рівень пояснюючої змінної X |
t |
визначає «бажаний» рівень залежної зміної Y * : |
||
|
|
|
t |
|
|
|
Y * =α + βX |
t |
(2.53). |
|
|
t |
|
|
Наприклад, бажаний рівень запасів фірми є функцією від рівня продаж, бажаний рівень капіталу в економіці є функцією випуску.
Однак, бажаний рівень не можна спостерігати і, отже, використовувати для оцінювання. Завдяки різним причинам існує різниця між бажаним і фактичним рівнями залежної зміної:
|
Y −Y |
=γ(Y |
−Y |
|
) +ε |
t |
(2.54) |
||
|
t |
t −1 |
|
|
t −1 |
|
|
||
Тобто, з |
точністю до |
збурення |
фактичний приріст залежної |
зміної |
|||||
Yt −Yt −1 є меньшим від бажаного в γ |
разів. |
|
|
|
|
||||
Рівняння |
(2.55) відоме |
як |
|
рівняння |
часткового пристосування, |
а γ |
|||
називається коефіцієнтом пристосування.
Чим γ ближче до одиниці, тим швидше фактичний рівень наближається
до бажаного. |
|
|
|
|
|
Запишемо (2.54) у такому вигляді |
|
|
|
||
Y |
= γY |
+( 1 −γ )Y |
+ε |
t |
(2.55) |
t |
t |
t −1 |
|
|
|
З (2.55) видно, |
що фактичне |
значення залежної змінної |
в момент |
||
t дорівнює зваженому |
середньому |
її |
бажаного |
значення в |
момент t і |
фактичному значенню в момент t −1. |
|
|
|
|
|
Підставимо (2.53) до (2.55): |
|
|
|
|
|
Yt =γ(α + βX t ) + ( 1 −γ )Yt −1 + εt |
|
|
|
|
|
Звідси |
|
|
|
|
|
|
Yt =αγ + βγX t |
+( 1 −γ )Yy−1 |
+ εt |
(2.56) |
|
Якщо не брати до уваги властивості збурень, то (2.56)є авторегресійною формою моделі з геометричним розподілом лагів.
2.6.2.Модель адаптивних очікувань
В моделі адаптивних очікувань, запропонованій Кейганом, «очікуваний»
рівень пояснюючої змінної X |
визначає поточний рівень залежної змінної Y : |
||||
|
t |
|
|
|
t |
|
Y =α + βX |
+ε |
t |
(2.57) |
|
|
t |
t |
|
|
|
Наприклад, сукупний |
попит на |
|
гроші є функцією |
очікуваної |
|
довгостркової відсоткової ставки, обсяг попиту є функцією очікуваної ціни, рівень споживання є функцією очікуваного або перманентного доходу.
Кейган припустив, що очікувані значення коректуються з урахуванням
нової інформації: |
|
|
|
|
|
|
|
|
|
X t − X t −1 |
= δ( X t |
− X t −1 |
), |
0 < δ ≤1 |
|
(2.58) |
|
Оскільки |
0 < δ ≤1 , |
то |
зміна |
очікуваного рівня |
X t − X t −1 |
є завжди |
||
меньшою ніж |
різниця |
між |
фпктичним |
значенням X t |
і його |
очікуваним |
||
значеням X t −1 .
Рівняння (2.58) відоме як «рівняння адаптивних очікувань» або «рівняння навчання на похибках».
Коефіцієнт δ називається «коефіцієнтом очікувань» . Чим більше δ , тим в більшій мірі реалізуються очікування в період t .
У крайньому випадку δ = 1 всі очікування реалізуються протягом поточного періоду.
Запишемо (2.58)у такому вигляді |
|
X t = δX t +( 1 −δ )X t −1 |
(2.59) |
звідки видно, що очікуване значення є зваженим середнім фактичного і
попереднього очікуваного значення. |
|
|
|
|
||
Підставимо (2.59) до (2.57): |
|
|
|
|
|
|
Y =α + βδX |
t |
+ β( 1 −δ )X |
+ε |
t |
(2.60) |
|
t |
|
t −1 |
|
|
||
Запишемо (2.60)для моменту |
t −1, результат помножимо |
на (1-δ ) і |
||||
віднімемо від (2.59): |
|
|
|
|
|
|
Yt =αδ + βδX t +( 1 −δ )Yt −1 + εt −( 1 −δ )εt −1 |
(2.61) |
|||||
Таким чином, ми одержали модель з геометрично розподіленими лагами, записану а авторегресійній формі. Якщо збурення у вихідній моделі (2.62) є класичними (тобто гомоскедастичними і некорельованими), то збурення в моделі, записаній у вигляді (2.61) генеруються процесом MA(1). Однак не слід думати, що модель адаптивних очікувань з необхідністю веде до появи автокорельованих збурень в авторегресійній формі моделі. Наприклад, якщо в
(2.57)
εt= (1-δ) εt-1+ut,
то ut являють собою збурення в моделі (2.61). Зрозуміло, що ut можуть бути некорельованими і гомоскедастичними. Оскільки апріорі невідомо, якими є властивості збурень вихідної моделі в конкретних ситуаціях, то зі сказаного можна зробити висновок, що та чи інша економічна модель, яка призводить до моделі з геометричними лагами, взята сама по собі, не визначає властивості збурень в авторегресійному вигляді останньої. Отже, на нашу думку, правильним підходом буде статистичне визначення властивостей збурень в кожній конкретній ситуації.
2.7. Оцінювання моделей з нескінченною довжиною лагів.
В цьому параграфі ми коротко і досить неформально розглянемо методи оцінювання моделей з раціональними лагами, приділяючи основну увагу найпростішому випадку – моделям з геометричним розподілом лагів. Відразу наголосимо, що необхідною умовою консистентності оцінок методу найменших квадратів і оцінок інших методів є стаціонарність змінних моделі. Отже, важливо пам’ятати, що моделі з розподіленими лагами є засобом дослідження зв’язків між стаціонарними змінними. В протилежному випадку в деяких випадках вдається відшукати “стабілізуючі” перетворення, такі як перехід до різниць (як це робиться при моделюванні Бокса–Дженкінса), або до відносних приростів. Звернімо увагу на те, що в прикладах, розглянутих на початку розділу, деякі змінні відразу розглядались у вигляді приростів, що диктувалось теорією, покладеною в основу відповідних моделей. Якщо змінні стають стаціонарними в результаті виділення детермінистичного тренду, наприклад, лінійного, то проблема вирішується шляхом включення в модель відповідного тренда. Найбільш уживаним способом дослідження залежностей між нестаціонарними змінними є модель корекції похибок.
Як зазначалось вище, моделі з (раціонально)розподіленими лагами можна записувати у двох формах: авторегресійній і рухомого середнього. Тому оцінювати модель можна в будь-якій з цих форм.
7.1. Оцінювання у авторегресійній формі.
Авторегресійна форма моделі з раціонально розподіленими лагами у випадку єдиної пояснюючої змінної має вигляд
k |
l |
|
|
Yt =α + ∑βi X t −i |
+ ∑γiYt −i |
+εt , |
(2.62) |
i=0 |
i=1 |
|
|
де εt – збурення, а кількості k–1 i l лагових значень визначаються на відміну від випадку необмежених лагів вихідним виглядом моделі (у формі рухомого середнього). Наприклад, як ми побачили в параграфі 6, авторегресійна форма моделі з геометричним розподілом лагів є такою
Yt =α + βX t + γYt −1 + εt , |
(2.63) |
а для лагів Паскаля з r=2 маємо:
Yt =α + β0 X t + β1 X t −1 + γ1Yt −1 + γ 2Yt −2 + εt . |
(2.64) |
Методи оцінювання залежать від стохастичної специфікації збурень. При виконанні класичних умов оцінки методу найменших квадратів будуть консистентними, хоча і зміщеними.
Складнішою буде ситуація у випаку автокорельованих збурень. В цьому місці буде доречним нагадати про некоректність використання критерія Дурбіна–Ватсона для перевірки автокорельованості збурень у випадку наявності лагових значень залежної змінної (див. параграф. 1.5.9)
У численних джерелах можна зустріти твердження про неконсистентність оцінок методу найменших квадратів за умов наявності лагових значень залежної змінної і автокорельованих збурень. Однак, без подальших уточнень, це твердження може виявитись хибним. Так, можна навести приклад структури автокореляції збурень в моделі (2.63), при якій Yt −1 виявляється некорельованим з εt . У такому випадку коректно застосувати звичайний метод найменших квадратів з використанням оцінки Неві–Веста для коваріаційної матриці оцінок параметрів. В інших випадках, наприклад для AR(1) - або для MA(1) – збурень в моделі (2.63), Yt −1 є корельованим з εt . В цій ситуації водночас найбільш простим у практичній реалізації і надійним з теоретичної точки зору є метод інструментальних змінних.
Інструментами для регресора X називаються змінні Z, які корельовані з X, але не корельовані з поточними збуреннями. Для знаходження оцінок потрібно відшукати принаймі не менше інструментів (які відсутні в моделі), ніж кількість ендогенних регресорів, тобто тих, які корельовані з поточними збуреннями. Техніку обчислень простіше за все описати так. Оцінювання здійснюється в два етапи. На першому етапі звичайним методом найменших квадратів оцінюються регресії ендогенних регресорів відносно інструментів, в число яких включають регресори моделі, некореьовані з поточними регресорами (екзогенні регресори). На другому етапі також звичайним методом найменших квадратів оцінюється вихідна модель, в якій значення ендогенних регресорів, замінюються на свої оцінки, знайдені на першому етапі.
