
Прикладна економетрика - Комашко О. В
.pdfутворюється незалежна виборка, а потім застосувати формулу щільності для
функції випадкових |
|
величин. Нехай |
yi = yi (x1 ,...,xn )i =1,n. |
|
Якщо існують |
|||||||||||||||||||
обернені функції xi = xi (y1 ,..., yn ),то |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
f y (y1 ,...yn )= |
|
J |
|
|
f x (x1 (y1 ,...yn ),...xn (y1 ,...yn ), |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
∂x |
(y |
|
,...y |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
де |
|
|
– Якобіан перетворення |
x |
|
= x |
|
(y |
|
,...,y |
|
),i =1,n . |
||||||||||||
J = det |
|
|
|
|
i |
|
1 |
|
n |
|
i |
i |
1 |
n |
||||||||||
|
|
|
|
|
|
|
∂y j |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Проілюструємо цей підхід на прикладах.
Проста лінійна регресія.
Нехай в моделі
|
|
|
|
yi = β0 |
+ β1 xi +εi ,i = |
|
|
|
|
|||||
|
|
|
|
1,n |
|
|
||||||||
збурення εi |
|
незалежні і однаково розподілені (i.i.d) з розподілом N (0,σ 2 ). Тоді |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
(ε |
|
|
|
)= |
1 |
|
∑εi |
|
||||
f |
|
|
,...ε |
|
exp− |
i=1 |
|
. |
||||||
ε |
1 |
n |
|
(2πσ 2 )n / 2 |
2σ 2 |
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перепишемо рівняння моделі в такому вигляді:
εi = yi |
− (β0 + β1 x1 ), |
i =1,n , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∂ε |
i |
= |
1, i = j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∂y j |
|
|
0, i ≠ j. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Таким чином, матриця перетворення є одиничною. Отже, |
|
J |
|
=1, а |
|
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
f y (y1 ,...y n |
|
β0 ,β1 ,σ 2 )= fε (ε1 ( y1 ,...yn ),...,εn ( y1 ,...yn ) |
|
β0 ,β1 ,σ 2 ) |
|
|
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
∑n (yi − (β0 + β1 xi ))2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
|
|
|
|
|
|
|
exp |
i=1 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||
(2πσ |
2 )n / 2 |
|
|
|
2σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ми |
|
|
|
|
показали, |
що |
функція |
правдоподібності |
має |
вигляд |
|||||||||||||||||||
L(β |
|
|
|
|
|
|
|
)= |
1 |
|
∑n (yi − (β0 |
+ β1 xi |
))2 |
|
|
||||||||||||||
|
,β |
|
,σ 2 |
|
exp |
i=1 |
|
|
|
|
., |
|
|
||||||||||||||||
0 |
1 |
(2πσ 2 )n / 2 |
|
|
2σ |
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
а її логарифм |
|
|
||||
l( β0 |
,β1 |
,σ 2 )= − |
n |
ln 2πσ 2 |
− |
Σ( yi − ( β0 ,β1 ,xi ) )2 . |
|
||||||
|
|
2 |
|
|
2σ 2 |
|
Запишемо необхідну умову існування екстремуму:
∂ln L |
=0, |
∂ln L |
=0, |
∂ln L |
=0. |
||
∂β |
0 |
|
∂β |
1 |
|
∂σ 2 |
|
|
|
|
|
|
|
||
Одержані рівняння називаються рівняннями максимальної правдоподібності. Якщо розписати ці рівняння, неважко побачити, що спочатку знаходяться розв’язки відносноβ0 і β1 , а потім відносно σ 2 . Причому, знаходження розв’язку еквівалентно мінімізації виразу
Σ ( yi − ( β0 + β1 xi ) )2 ,
який є знайомою сумою квадратів залишків. Тобто ММП –оцінки параметрів регресії - β0 і β1 у випадку нормально розподілених збурень співпадають з оцінками найменших квадратів. В даному випадку функцію спільної щільності
можна було |
записати |
безпосередньо, враховуючи |
той факт, |
що |
||||||||||
yi |
~ N( α + βxi ,σ 2 ) і yi незалежні. Другий підхід зручніше використовувати, |
|||||||||||||
якщо спостереження залежної змінної незалежні, а перший – якщо залежні. |
|
|||||||||||||
|
|
|
Процес АR(1). |
|
|
|
|
|
|
|
||||
|
|
|
Нагадаємо, що модель має вигляд |
|
|
|
|
|
|
|||||
|
|
|
yi = ρyi−1 + εi , |
|
|
|
|
|
|
|
||||
де |
|
|
ρ |
|
<1 , а εi |
− i.i.d і мають розподіл |
N( 0,σ 2 |
). Від |
y1 ,...yn перейдемо до |
|||||
|
|
|||||||||||||
y1 |
,ε2 ,...,εn . |
Зауважимо, |
що |
y1 ~ N ( 0 |
σ 2 |
|
),εi |
~ N ( 0,σ 2 ) |
і |
|||||
1 − ρ2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
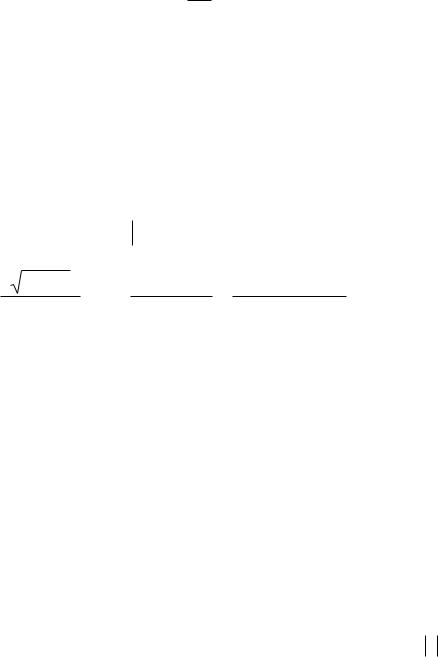
y1 ,ε2 ,...,εn .незалежні. Для i = 2,n εi = yi − ρyi−1 , тому Якобіан перетворення має
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ρ1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
вигляд J = |
|
|
... |
|
|
=1 . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
1 |
|
|
|
|
|
|
|
|
|
Отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
L( ρ,σ 2 ) = L( ρ,σ 2 |
y1 ,...yn ) = f y ( y1 ,...yn |
) = |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
1 − |
ρ |
2 |
|
|
y |
( 1 − ρ |
2 |
) |
∑( yi − |
ρyi−1 )2 |
|
|
|||
= |
|
|
exp( − |
|
− i=2 |
|
|
). |
|
|
|||||||||
|
( 2πσ 2 |
)n / 2 |
1 |
2σ 2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2σ |
2 |
|
|
|
||||||
Процес МА (1). |
|
|
|
|
|
|
|
|
|
|
|||||||||
Модель має вигляд |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
yi =εi −θεi−1 , |
|
|
|
|
|
|
|
|
|
|
|||||
де |
|
θ |
|
<1,εt |
− i.i.d |
і |
|
мають |
розподіл |
|
N( 0,σ 2 ). В |
цьому |
випадку |
||||||
|
|
|
|
||||||||||||||||
t −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
εt = ∑θ j yt − j |
+θ t ε0 . |
|
|
|
|
|
|
|
|
|
|
||||||||
j=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Однак |
ε0 |
|
не |
спостерігається і |
|
не виражається |
через |
значення |
|||||||||||
спостережень. Тому в цьому і подібних випадках використовують умовну функцію правдоподібності покладаючи ε0 =0 . Оскільки θ <1,то θt →0 при t → ∞, а отже, умовна функція правдоподібності практично не відрізняється від точної функції правдоподібності. Якобіан перетворення також дорівнює 1, тому
L(θ,σ 2 ) = |
1 |
|
exp(− |
1 |
∑n |
εi2 |
). |
|
|
n−1 |
|
2 |
|||||
|
( 2πσ 2 ) |
|
|
|
2 i=2 σ |
|||
|
2 |
|
||||||
1.6.3. Асимптотичні властивості ММП-оцінок.
Широкому використанню в економетриці ММП завдячує саме cвоїм асимптотичним властивостям. Позначимо черезθˆML ММП-оцінку θ .
1.Консистентність: plimθˆML =θ . Через plim позначено границю за
ймовірністю.
2.Асимптотична нормальність θˆ N(θ,{ I(θ )}−1 ) , де символ “ ”
означає збіжність за розподілом, N(m, Σ) – багатовимірний нормальний розподіл з вектором математичних сподівань m і коваріаційною матрицею Σ.
Через I(θ) позначено інформаційну матрицю:
−1 |
∂2 ln L(θ ) −1 |
|
∂ln L(θ ) |
|
∂ln L(θ ) |
|
−1 |
||||
[I(θ )] |
={ −E |
|
|
|
} ={ E |
|
( |
|
|
) . |
|
∂θ∂θ |
' |
∂θ |
∂θ′ |
||||||||
|
|
|
|
|
|
|
|
||||
3. Асимптотична ефективність. ММП-оцінки досягають границі Крамера-Рао для консистентних оцінок:
AsyVar(θˆML |
∂2 ln L(θ ) −1 |
|
∂ln L(θ ) |
( |
∂ln L(θ ) |
|
−1 |
|||
) ={ −E |
∂θ∂θ |
' |
|
} ={ E |
∂θ |
∂θ′ |
) |
, |
||
|
|
|
|
|
|
|
|
|||
де через AsyVar позначається асимптотична каріаційна матриця.
Слід підкреслити, що точні скінченновимірні властивості ММП-оцінок, як правило, є невідомими, і в деяких випадках, ці оцінки не є найкращими для малих виборок.
4. Інваріантність. Якщо g(θ ) є неперервною функцією, то g(θˆML ) є
ММП-оцінкою g(θ ).
1.6.4. Оцінювання дисперсії ММП-оцінок.
У багатьох випадках другі похідні логарифму функції правдоподібності мають досить складний вигляд, тому знайти їх математичні сподівання виявляється неможливим. На практиці використовують два способи. Перший полягає в обчислені відповідних похідних при значеннях аргументів, які дорівнюють ММП-оцінкам
ˆ |
ˆ |
∂2 LnL(θˆ ) |
−1 |
||
D(θ )− |
ˆ ˆ |
′ |
. |
||
|
|
∂θ∂θ |
|
|
|
Друга оцінка грунтується на тому, що математичне сподівання матриі других похідних дорівнює коваріаційній матриці перших похідних:

Dˆ (θˆ ) ∑i gˆ i gˆ i' −1 ,
де |
g |
= |
∂ln f (yi ,θ ) |
. |
|
||||
|
ˆ i |
|
∂θˆ |
|
|
|
|
||
1.6.5.Три асимптотично еквівалентні критерії перевірки гіпотез.
1.Критерій відношення правдоподібності (LR).
Нехай θ -вектор параметрів моделі. Нехай гіпотеза Η 0 визначає сукупність обмеженнь на значення параметрів. Нехай θˆu - ММП-оцінка, знайдена в моделі без обмежень, θˆr - ММП-оцінка, знайдена в моделі з обмеженням. Нехай Lˆ u ,Lˆ r
означають значення функцій правдоподібності для необмеженої і обмеженої моделей, знайдені в точках θˆu iθˆr відповідно . При виконанні достатньо необмежливих умов регулярності статистика
LR = −2ln Lˆ r Lˆ u
асимптотично має розділ χ - квадрат з кількістю степенів свободи, рівною кількості обмежень. Недоліком критерія є необхідність оцінювати модель в обох випадках – без обмежень і з обмеженнями.
2.Критерій Вальда.
Запишемо гіпотезу про сукупність обмежень у такому вигляді Η 0 : c(θ )= q. За умови, що обмеження вірні. Статистика Вальда
W = (c(θˆ )− q)' (D[c(θˆ ) − q])−1 (c(θˆ ) − q).
асимптотично має розподіл χ -квадрат з кількістю степенів свободи,
рівною кількістю обмежень (тобто кількості рівнянь в c(θ )= q ). Зауважимо, що у випадку коли обмеження є нелінійними, то коваріаційну матрицю c(θ )
оцінюють наступним числом
D[c(θˆ )− q]≈CDθˆC' ,

де C = ∂∂cθ(ˆθˆ' ) ,
тобто j − й рядок матриці С складають похідні j − го обмеження відносно всіх елементів θ . У випадку лінійних обмежень Rθ = q . статистика Вальда набуває
вигляду
W = [Rθˆ − q][' RDθˆR']−1 [Rθˆ − q].
Кількість степенів свободи дорівнює кількості рядків в матриці R. Критерій можна застосувати не тільки для ММП-оцінок, але і для будь-яких консистентних асимптотично нормальних оцінок. Для перевірки гіпотези потрібно мати оцінки тільки в моделі без обмежень. Недоліком критерія є неінваріантність його статистики відносно форми запису обмежень.
3.Критерій множників Лагранжа (LM).
Як і в попередньому випадку запишемо гіпотезу у вигляді. Η 0 : c(θ )= q.
Для застосування цього критерію, потрібно знати оцінку θˆr в моделі з обмеженнями і записати функцію правдоподібності в моделі без обмеженнь. Статистика критерію
LM = ∂ln∂Lθˆ(rθˆr ) / [I(θˆr )]−1 ∂ln∂Lθˆ(rθˆr )
асимптотично має розподіл χ -квадрат з кількістю степенів свободи, рівною кількості обмежень.
Вибір критерія, як правило здійснюється з огляду на те, який з них простіше застосувати. Перевіряючи нелінійні обмеження, при можливості уникають використання критерія Вальда внаслідок його неінваріантності.
РОЗДІЛ 2. МОДЕЛІ З ЛАГОВИМИ ЗМІННИМИ
Ключові поняття:
Моделі зі скінченною довжиною лагів (D-L); Моделі з нескінченною довжиною лагів (D-L);
Моделі часткового пристосування і адаптивних очікувань
2.1. Приклади з економічної теорії
У большості ситуацій вплив більшості факторів не відчувається миттєво.Час, який потрібен для того, щоб дія фактора реалізувалася у повній мірі залежить від характеристик і складнощі явища, яке аналізується. Розглянемо декілько економічних прикладів.
Приклад 2.1. Функція споживання.
Найпростіша лінійна функція споживання маї вигляд
|
|
Ct =α0 + β0Yt + ut |
(2.1) |
Де |
Ct - особисте споживання; |
|
|
Yt - особистий доход у роспорядженні; |
|
||
ut - збурення; |
|
||
α0 ,β0 - параметри, α0 > 0 , 0 < β0 < 1 . |
|
||
|
|
Частка Ct / ut - це «середня схильність до споживання», а перша похідна |
|
|
∂Ct |
= β0 є граничної схильністю до споживання. |
|
|
∂ut |
|
|
|
|
|
|
З рівняння (2.1) випливає, що поточне значення споживання залежить тольки від поточного значення доходу та не залежить від поточних значень будь-яких інших значень.
Однак, така спеціфікація моделі може біти некоректною. Наприклад, поточне споживання може також залежить від поточного рівня накопичень. В такому віпадку функція споживання набуде такого вигляду
Ct =α0 + β0Yt +γ 0 St + ut |
(2.2) |
де St - особисті накопичення
γ0 - параметр моделі.
Як відомо з економічної теорії, поточний рівень накопичень залежить від доходу в минулому році. Тому функцію накопичень можна записати так
St =δ0 + δ1Yt −1 + δ2Yt −2 + ... +υt |
(2.3) |
|
де δ j (для j=0,1,...) - параметри моделі; |
|
|
υt - збурення. |
|
|
Підставимо (2.3) до (2.2) та одержимо |
|
|
Ct =(α0 +γ0δ0 ) + β0δ1Yt −1 + β0δ2Yt −2 |
+ ... +( γ0υt + ut |
) |
або |
|
|
Ct = α + β0Yt + β1Yt −1 |
+ β2Yt −2 ... + εt |
(2.4) |
З рівняння (2.4) випливає, що поточний рівень споживання залежить від поточного та минулого значень доходу.
Якщо прийняти до уваги так званну постійность звичок, то поточний рівень споживання залежить від минулих рівней споживання;
Ct = α + β0Yt + β1Yt −1 + β2Yt −2 ... +α1Ct −1 +α2 Ct −2 + ... + εt |
(2.5) |
Приклад 2.2.
У найпростішій акселераторній моделі інвестицій стверджується, що існує зв’язок між чистими інвестиціями і зміною випуску. Це взаємовіднршення можна записати у вигляді;
It = β0 X t + εt |
(2.6) |
Де It - чисті інвестиції;
X t = Qt −Qt −1 ;
Qt - випуск;
β0 - параметр.
Змоделі випливає, що рівень інвестицій буде значно коливатися. Інвестиції будуть додатніми, якщо економіка на підйомі (Qt −Qt −1 > 0 ) і
від’ємними, якщо економіка на спаді (Qt − Qt −1 < 0 ). Однак зміна рівня
інвестицій залежить і від інших факторів, наприклад, від розподілу в часі інвестиційних рішень.
Оскільки інвестиційні рішення за різники причинами можуть відкладатися, реакція інвестицій на зміну випуску розповсюджується в часі. В цьому випадку рівняння (2.6) можна записати так;
It = β0 + β1 X t −1 + β2 X t −2 ... + βk X t −k +εt |
(2.7) |
Приклад 2.3. Кількісна теорія грошей.
Кількісна теорія грошей стверджує, що рівень цін в економіці пропорційний до обсягу грошової маси в цій економіці. Це твердження випливає з рівняння Ірвінга Фішера (1867-1947);
|
|
|
|
|
|
|
|
|
|
|
|
|
M tVt = Pt Qt |
, |
(2.8) |
||
Де M t - номінальний обсяг грошової маси: |
|
|
|
||||||||||||||
Vt - швидкість обігу грошей: |
|
|
|
||||||||||||||
Qt |
- реальний випуск (обсяг кінцевих товарів та послуг): |
|
|||||||||||||||
Pt |
- |
|
загальний рівень цін. |
|
|
|
|||||||||||
|
|
|
Прологарифмуємо співвідношення (2.8) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln M t + lnVt |
= ln Pt +ln Qt |
(2.9) |
|||
|
|
|
В результаті диференціювання (2.9) за часом одержимо |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
mt + vt |
= pt |
+ qt , |
(2.10) |
|
де x |
t |
= |
∂ |
|
ln X |
t |
= |
1 |
|
∂X t |
. |
|
|
|
|
|
|
∂t |
|
|
|
|
|
||||||||||||
|
|
|
|
|
X t ∂t |
|
|
|
|||||||||
|
|
|
У випадку дискретного часу замість похідних розглянемо відносні |
||||||||||||||
прирісти; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
X t − X t −1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X t |
|
|
|
|
|
|
|
Перепишемо (2.10) у такому вигляді; |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
pt = mt − qt + vt |
(2.11). |
|||
Таким чином, інфляція визначається зміною реального випуску, зміною номінальної грошової маси і зміною швидкості обігу грошей.
Монетаристи стверджують, що основним фактором, який визначає інфляцію є зміна грошової маси, вважаючи два інших фактори неважливими. В залежності від того, буде сумарний ефект змін випуску і швидкості обігу позитивним, нульовим чи додатнім інфляція буде більшою, рівною або меншою ніж зміна грошовоє маси.
Отже, з монетаристської точки зору, залежність інфляції від обсягу грошей буде такою;
pt =α + β0 mt + εt . |
(2.12) |
Тоді як, з рівняння (2.12) випливає, що зміна грошової маси діє на інфляцію миттєво, в реальності реакція інфляції розподілена в часу. Тому залежність (2.12) необхідно записати у вигляді:
pt =α + β0 mt + β1mt−1 + β2 mt−2 + ... + εt |
(2.13) |
Приклад 4.4. Крива Філіпса.
Крива Філіпса у первісному вигляді описує емпіричне співвідношення між відносною зміною заробітної платні і безробіттям у відсотках до загальної кількості робочої сили. Чим вище рівень безробіття, тим менше зміна заробітної платні.
Це співвідношення можна записати так;
w =αU β eεt |
(2.14) |
|
t |
t |
|
Де wt = ( wt − wt −1 )wt −1 ;
wt - рівень заробітної платні;
Ut - рівень безробіття у відсотках; εt - збурення;
αt > 0,βt > 0 - параметри.
Припустимо, що заробітна платня залежить також від цін у минулому. Крім того, врахуємо, що реакція заробітної платні не є миттєвою. Тоді замість (2.14) слід записати
w |
=αU β |
...U βm |
...pγ1 |
...pγk |
eε |
t |
(2.15) |
t |
t |
t −m |
t −1 |
t −k |
|
|
