
Прикладна економетрика - Комашко О. В
.pdf21
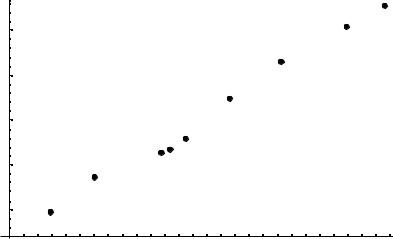
В Таблиці 1.1. наведено обсяги сукупного доходу у розпорядженні та сукупного споживання для США у постійних доларах 1972 р. Дані з Таблиці 1.1. зображено графічно на на Рис.1.3. З графіка видно, що точки, які відповідають спостереженням, розташовані навколо деякої прямої, отже доцільно розглянути лінійну функцію споживання. Оцінимо її за допомогою моделі простої лінійної регресії:
yi = α + βxi + εi , i = |
|
, |
(1.27) |
110, |
де через xi та yi позначено відповідно рівень доходу і споживання в році 1969 + i (наприклад i = 5 відповідає 1974 року). Спочатку обчислимо
Таблиця 1.1.
Рік |
Доход у розпорядженні |
Особисте споживання |
|
|
|
1970 |
751,6 |
672,1 |
1971 |
779,2 |
696,8 |
1972 |
810,3 |
737,1 |
1973 |
864,7 |
767,9 |
1974 |
857,5 |
762,8 |
1975 |
874,9 |
779,4 |
1976 |
906,8 |
823,1 |
1977 |
942,9 |
864,3 |
1978 |
988,8 |
903,2 |
1979 |
1015,7 |
927,6 |
|
|
|
22
Споживання
900
850
800
750
700



























 Доход
Доход
800 |
850 |
900 |
950 |
1000 |
Рис. 1.3.
x =(751,6+779,2+810,3+864,7+857,5+874,9+906,8+942,9+988,8+1015,7)/10 = = 879,24;
y =(672,1+696,8+737,1+767,9+762,8+779,4+823,1+864,3+903,2+927,6)/10 = = 793,43;
Sxx = ((751,6 – 879,24)2 + (779,2 – 879,24)2 + (810,3 – 879,24)2 +
+(864,7 – 879,24)2 + (857,5 – 879,24)2 + (874,9 – 879,24)2 +
+(906,8 – 879,24)2 + (942,9 – 879,24)2 + (988,8 – 879,24)2 +
+(1015,7879,24)2 ) = 67192,4;
Syy = ((672,1 – 793,43)2 + (696,8 – 793,43)2 + (737,1 – 793,43)2 +
+(767,9 – 793,43)2 + (762,8 – 793,43)2 + (779,4 – 793,43)2 +
+(823,1 – 793,43)2 + (864,3 – 793,43)2 + (903,2 – 793,43)2 +
+(927,6 – 793,43)2 ) = 64972,1;
Sxy = ((751,6 – 879,24) (672,1 – 793,43) + (779,2 – 879,24) (696,8 – 793,43) + + (810,3 – 879,24) (737,1 – 793,43) + (864,7 – 879,24) (767,9 – 793,43) +

23
+(857,5 – 879,24) (762,8 – 793,43) + (874,9 – 879,24) (779,4 – 793,43) +
+(906,8 – 879,24) (823,1 – 793,43) + (942,9 – 879,24) (864,3 – 793,43) +
+(988,8 – 879,24) (903,2 – 793,43) + (1015,7879,24) (927,6 – 793,43) ) = = 65799,3.
За формулами (1.7) знаходими оцінки методу найменших квадратів коефіцієнгів моделі (1.27):
b = |
S xy |
= |
65799,3 |
= 0,979; |
|
S xx |
67192,4 |
||||
|
|
|
a = y − bx = 793,43 − 0,979 × 879,24 = -67,58.
Отже, рівняння вибіркової регресійної прямої (рівняння фунцції споживання) має вигляд:
y$ = – 67,58 + 0.979x. |
(1.28) |
Споживання |
|
|
|
|
900 |
|
|
|
|
850 |
|
|
|
|
800 |
|
|
|
|
750 |
|
|
|
|
700 |
|
|
|
Доход |
800 |
850 |
900 |
950 |
1000 |
Рис 1.4 |
|
|
|
|
Графік цієї прямої зображено на Рис. 1.4. разом з фактичними даними.
Щоб мати уявлення про тісноту зв’язку між доходом і споживанням, обчислимо коефіцієнт детемінації.
За формулою (1.17а) маємо:
R 2 = bSxy/Syy = = 0.979×65799,3/64972,1 = 0.990702.
Як ми бачимо, зв’язок між споживанням і доходом є вельми тісним. Перед тим, як використовувати рівняння (1.28) для економічного аналізу або
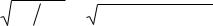
24
побудови прогнозів, модель (1.27) потрібно перевірити на адекватність. Перевіримо гіпотезу про значущість регресії двома способами. Спочатку використаємо F-статистику (1.23):
|
|
|
R2 |
|
|
|
|
0.990702 |
|
|
|
F = |
|
1 |
|
|
= |
1 |
|
= 959,917 . |
|||
|
− R2 |
|
1 − 0.990702 |
||||||||
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
8 |
|
|
|
|
n − 2 |
|
|
|
|||||||
Нехай, рівень значущості α дорівнює 0,05. В Таблиці 3. Додатку знаходимо, що критичне значення F кр = 5,32. Ми бачимо, що |F|≥Fкр, отже гіпотеза про рівність
β нулю відхиляється, тим самим модель (1.27) є значущою.
Обчислимо стандартні похибки оцінок. Спочатку знайдемо суму квадратів залишків RSS. За формулою (1.15)
RSS = Syy – b2Sxx = 64972,1 – 0.9792×67192,4 = 537,0.
Далі знаходимо оцінку дисперсії збурень
σ$ 2 |
= |
RSS |
|
= |
537,0 |
= 67,13. |
|
n − 2 |
8 |
||||||
|
|
|
|
||||
Стандартна похибка b дорювнює: |
|
|
|
|
|||
SE(b) = σ$ 2 |
Sxx |
= |
67,13 / 67192,4 =0.0316071. |
||||
Перевіримо гіпотезу про те, що коефіцієнт нахилу регресійної прямої β дорівнює нулю за допомогою t-статистики (1.20):

25
t = |
b |
= |
0.979 |
= 30.9825. |
|
SE(b) |
0.0316071 |
||||
|
|
|
Нехай, рівень значущості α дорівнює 0,05. В Таблиці 1. Додатку знаходимо, що критичне значення tкр = 2,306. Ми бачимо, що |t|≥tкр, отже гіпотеза відхиляється.
Отже, ми можемо вважати модель адекватною (читач не повинен забувати, що повна перевірка моделі на адекватність включає аналіз залишків, з елементами якого ми ознайомимось в розділах 3 та 4).
З теорії споживання відомо, що коефіцієнт нахилу лінійної функції споживання є маргінальною або граничною схильністю до споживоння. Таким чином, ми встановили, що в середньому 0.979×100 = 97,9% прирісту доходу витрачається на споживання1). Обчислене значення граничної схильності до споживання знаходиться в інтервалі (0; 1), що узгоджується з економічною теорією.
1) Слід зазначити, що лінійні функції споживання у вигляді (1.27) не розглядаються в серйозних дослідженнях починаючи з 50-х років, тому наведені результати мають лише учбове значення.

21
1.2. Множинна лінійна регресія
1.2.1. Опис моделі
За допомогою моделі простої лінійної регресіїї ми вивчали зв’язок між залежною змінною y та незалежною змінною x. Модель множинної лінійної регресії описує співвідношення між y та набором незалежних змінних x0, x1,
...,xk-1. Так, наприклад, при дослідженні попиту нас цікавить залежність обсягу попиту на деякий товар від ціни на цей товар, цін на взаємозамінні з даним товари та від доходів споживачів. При наявності n спостережень модель
множинної лінійної регресії записується у вигляді
yi = β0 xi0 + β1xi1 +K+βk−1xi,k−1 + εi ,i = |
|
(1.29) |
1, n |
де xij– значення j-ї незалежної змінної (xj) в i-му спостереженні, збурення εi задовольняють тим самим припущенням, що і в моделі простої регресії.
1.Нульове середнє: Eεi = 0, i =1, n .
2.Рівність дисперсій: Dεi = E ε2i = σ2 = const, i =1, n .
3.Незалежність збурень: εі та εj незалежні при i ≠ j .
4.Незалежність збурень та регресорів: xij та εі незалежні для всіх i та j (якщо регресори не стохастичні , то дане припущення виконується автоматично).
5.(Додаткове). Збурення εi нормально розподілені для всіх i.
Модель множинної лінійної регресії (1.29) зручно записувати у матричновекторному вигляді:
y = Xβ + ε |
(1.30) |
з використанням наступних позначень:

22
y1
y= y.2 –вектор значень залежної змінної,
y.n
x10
x20
X = xn0
x |
|
|
|
x |
|
|
|
|
|
x11 |
|
x1,k−1 |
|
|
|
|
|
||
21 |
|
|
|
2,k−1 |
|
|
|
|
|
|
|
|
|
|
|
|
– матриця значень незалежних змінних, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn1 |
|
xn,k−1 |
|
|
|
|
|||
|
|
|
|
ε1 |
|
|
|||
|
|
|
|
ε |
2 |
|
|
||
|
|
|
|
|
|
|
– вектор збурень, |
||
|
|
|
|
ε = |
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
εn |
|
|
|||
β0
β= β1 – вектор параметрів (коефіцієнтів) регресії.
βk−1
Матриця X складається з n рядків – відповідно до кількості спостережень, – і з k стовпчиків, кількість яких дорівнює кількості незалежних змінних. Щоб записати модель з константою:
yi = β0 + β1xi1 +K+βk−1xi,k−1 + εi ,i =1, n
у матричному вигляді, розглядають матрицю значень незалежних змінних, в якій перший стовпчик складається з одиниць:

23
1 |
x |
|
|
|
x |
|
|
1 x11 |
|
x1,k−1 |
|
||||
|
|
21 |
|
|
|
2,k−1 |
|
X = |
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 xn1 |
|
xn,k−1 |
|||||
Позначимо через Dε коваріаційну матрицю вектора збурень
|
Dε |
1 |
|
|
Cov(ε |
1 |
,ε |
2 |
) |
Cov(ε |
1 |
,ε |
3 |
) |
|
|
|
Cov(ε |
1 |
,ε |
n |
) |
|
||||||
|
Cov(ε |
|
|
) |
|
|
|
Cov(ε |
,ε |
) |
|
|
|
Cov(ε |
,ε |
|
|
||||||||||||
Dε = |
2 |
,ε |
1 |
Dε |
2 |
|
|
2 |
3 |
|
2 |
3 |
) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Cov(εn ,ε1 ) |
Cov(εn ,ε2 ) |
|
|
|
|
|
|
|
|
|
Dεn |
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
Eε1ε2 Eε1ε3 |
Eε1εn |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Eε1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Eε2ε1 |
|
Eε22 |
|
|
Eε2ε3 |
Eε2ε3 |
|
= |
E(εε |
T |
) , |
|
|
|
|
|||||||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eεn ε2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eεn ε1 |
|
|
|
|
Eεn |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
внаслідок того, що збурення мають нульові математичні сподівання. Тоді припущення 2 та 3 зручно записувати у вигляді:
Dε=σ2In, |
(1.31) |
де In– одинична матриця n-го порядку, а припущення 1 – Eε = 0.
Модель множинної лінійної регресії у матрично-векторних позначеннях:
y = Xb + ε, Eε = 0,
Dε = σ2I,
ε не залежить від X Додаткове припущення:

24
ε~N(0,σ2I)
1.2.2. Знаходження параметрів регресії методом найменших квадратів
Нехай β$ = (β$0 ,β$1,...,β$k−1 )T –деяка оцінка вектора параметрів β . Запишемо рівняння вибіркої регресії
y$ = β$0 x0 + β$1x1 +K+β$k−1xk−1 .
Тоді
y$i = β$0 xi0 + β$1xi1 +K+β$k −1xi,k−1
є |
оцінкою Eyi, побудованою на основі вибіркової регресіїї. Залишки |
ε$i |
визначаються як різниці між значеннями залежної змінної, які спостерігались, |
і обчисленими з регресії:
ε$i = yi − y$i .
Вектор залишківε$ дорівнюєε$ = y − y$ , де y$ = ( y$1, y$2 ,K, y$n )T , y$ = Xβ$ .
Оцінки методу найменших квадратів знаходяться з умови мінімізації суми квадратів залишків за всіма можливими значеннями β$
n
Q = Q(β$) = ∑ε$2i =(ε$T ,ε$) (1.32)
i=1
Щоб мінімізувати вираз (1.32), запишемо необхідну умову екстремуму,
тобто прирівняємо похідні відносно β$ до нуля. Маємо

25
∂∂Qβ$ = −2XT y + 2XTXβ$ = 0 ,
тобто, система нормальних рівнянь має вигляд
XT Xβ$ = XT y ,
звідки
β$ = (XTX)−1 XTy . |
(1.33) |
Перевірка достатніх умов екстремуму показує, що β$ , обчислена за (1.33),
дійсно мінімізує функцію (1.32). Надалі оцінку вектора коефіцієнтів моделі множинної лінійної регресії позначатимемо латинською літерою b,
|
b |
|
|
|
b0 |
|
|
|
1 |
|
|
b = |
|
. |
|
|
|
|
|
|
|||
|
|
bk −1
Оцінка методу найменших квадратів коефіцієнтів моделі моделі множинної лінійної регресії знаходиться за формулою:
b = (XT X)−1 X T y |
(1.34) |
|
|
Рівняння вибіркої регресії приймає вигляд
y$ = b0 x0 + b1 x1 +K+bk −1 xk −1 . |
(1.35), |
або, у випадку регресії з костантою,
