1.4. Пример построения и исследования математической

модели

Рассмотрим решение задачи: Моторная лодка прошла 25 км по течению реки и 3 км против течения, затратив на весь путь 2 часа. Какова скорость лодки в стоячей воде, если скорость течения реки 3 км/ч.

Здесь вместо реального объекта мы имеем дело с текстовой задачей, представляющей содержательную модель этой задачи, на основе которой строим её математическую модель. Пусть км/ч – скорость лодки в стоячей воде. Тогда скорость лодки по течению км/ч, а против течения  км/ч. По течению реки лодка прошла 25 км за ч, а против течения 3 км за ч. Значит, время, затраченное на весь путь, выраженное через неизвестное , будет ч, но по условию на весь путь затрачено 2 ч. Следовательно,

. (1.1)

Вот это уравнение и есть математическая модель задачи, возможно и неполная, но отражающая самую существенную связь условий задачи. Конечно, в дальнейшем может возникнуть необходимость дополнить модель неучтёнными ограничениями. Подчеркнём, что в уравнении (1.1) – безразмерная, неименованная величина. В математической модели мы отвлекаемся от физического смысла рассматриваемых величин: для нас важны числа, которыми эти величины выражаются. (Физические, размерные величины вновь будут важны на этапе анализа решения математической задачи, в нашем случае уравнения (1.1), и записи ответа в терминах исходной задачи).

Итак, на первом этапе мы свели решение текстовой задачи к математической задаче решения уравнения (1.1).

На втором этапе решаем математическую задачу, т.е. уравнение (1.1) и получаем два корня: (Ответ для модели – это внутримодельное решение). Кстати, это решение легко увидеть на графике функции , построенного с помощью компьютера для (рисунок 1.1). Этот график пересекает ось абсцисс в двух точках: и , функция непрерывна и убывает на каждом из двух положительных интервалах оси абсцисс, разделённых точкой . (Конечно, уравнение (1.1) можно привести к квадратному и решить его обычным способом).

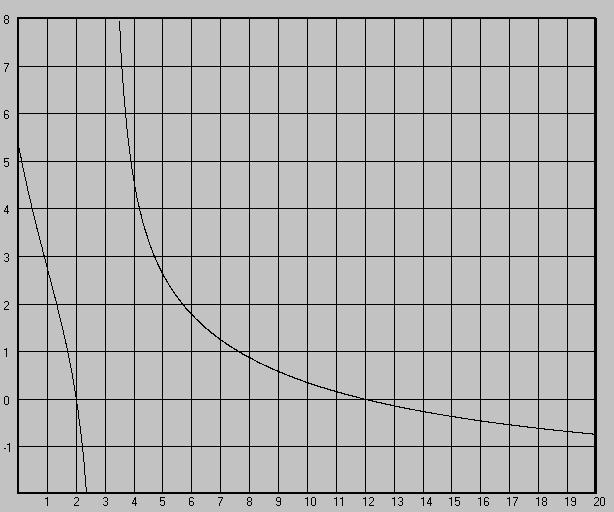
Рисунок 1.1 – Графическое решение уравнения (1.1)

На третьем этапе, имея уже решение математической задачи, необходимо это решение проанализировать, разобраться в его содержательном смысле и сделать правильные выводы. При этом следует иметь в виду, что уравнение (1.1) есть следствие исходной задачи и потому может содержать посторонние решения. Действительно, удовлетворяет уравнению (1.1), но не удовлетворяет условию задачи, так как скорость лодки 2 км/ч не может быть меньше скорости течения реки 3 км/ч. Итак, ответ, записанный в терминах исходной задачи: скорость лодки в стоячей воде равна 12 км/ч.

Теперь очевидно, что при построении математической модели мы не учли ограничение по условию задачи на скорость лодки в стоячей воде:

. (1.2)

Если учесть это условие, то из графика (рисунок 1.1) очевидно, что уравнение (1.1) имеет единственное решение.

Таким образом, полностью формализованной математической моделью рассматриваемой задачи является смешанная система, состоящая из уравнения (1.1) и неравенства (1.2). Именно эта система является математической записью физических условий, однозначно определяющих скорость лодки в стоячей воде.

В этой модели скорость – величина постоянная, не зависящая от времени. Такого типа модели называют статическими. А вот решение задачи: «Катер движется в спокойной воде со скоростью 20 км/ч. На полном ходу его мотор выключается и за 40 с скорость катера уменьшилась до 8 км/ч. Сопротивление воды пропорционально скорости движения катера. Определить скорость катера через две минуты после остановки мотора» требует построения динамической (эволюционной) математической модели, определяющей зависимость скорости катера от времени.

При решении прикладных задач очень важным является третий этап, заключающийся в обратном переводе результата исследования модели с языка математики на язык прикладной задачи, этап интерпретации (истолкования) результата исследования математической модели, этап, на котором нужно разобраться в решении математической задачи, в реальном смысле этого решения и сделать правильные выводы.

Например, широко известный многим ответ «два землекопа и » к школьной задаче из стихотворения С. Я. Маршака, который интерпретирует эти как человека «без ног, без головы», при таком толковании, конечно же, является бессмысленным. Но быть может (условие не приведено), речь шла о числе землекопов, необходимом для выполнения работы за рабочий день? Тогда результат можно истолковать так, что третий землекоп должен был работать рабочего дня [24, с.128]. При такой интерпретации ответ имеет реальный смысл.